Introduction to Double Number Lines
Opening
Introduction to Double Number Lines
Read and Discuss
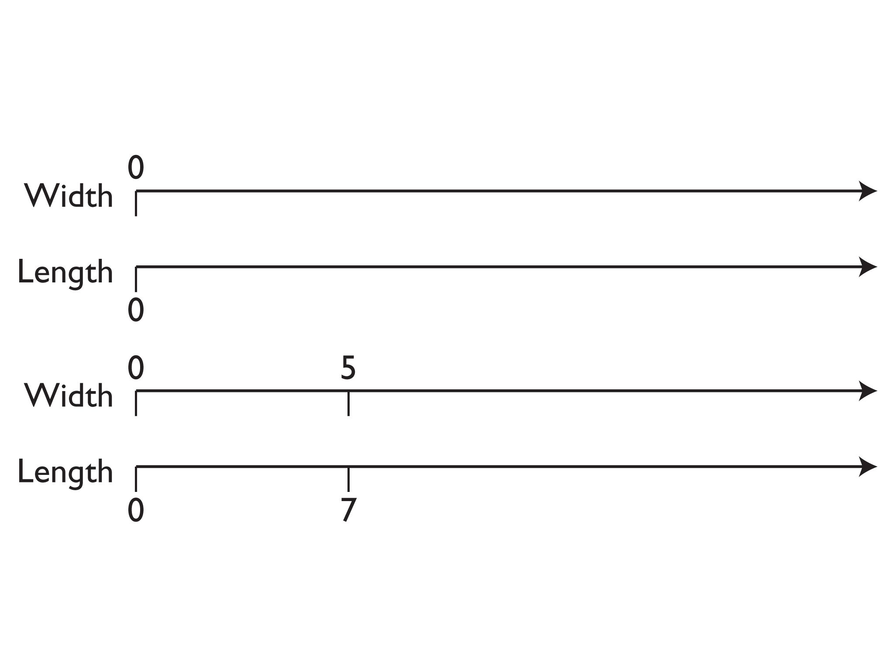
A company will enlarge 5-inch-by-7-inch photographs to any size you want.
You can use a double number line to help you see some of the possible photograph sizes.
- To make a double number line, you start with two number lines and line them up at 0.
- You know that the ratio of the width of the original photograph to its length is 5:7, so you would make one tick mark on the top line at 5 and another tick mark on the second line at 7, making sure that the 5 and 7 are lined up.
- Now you can add other numbers to the number lines.
- What are some of the possible photograph sizes you can order?
- What is another pair of numbers that would line up on this double number line?
- What does each lined-up pair of numbers represent? (Think of the question from the problem.)