Sports Reporters
One of the most famous soccer stadiums in the world is the Estadio Azteca in Mexico City.
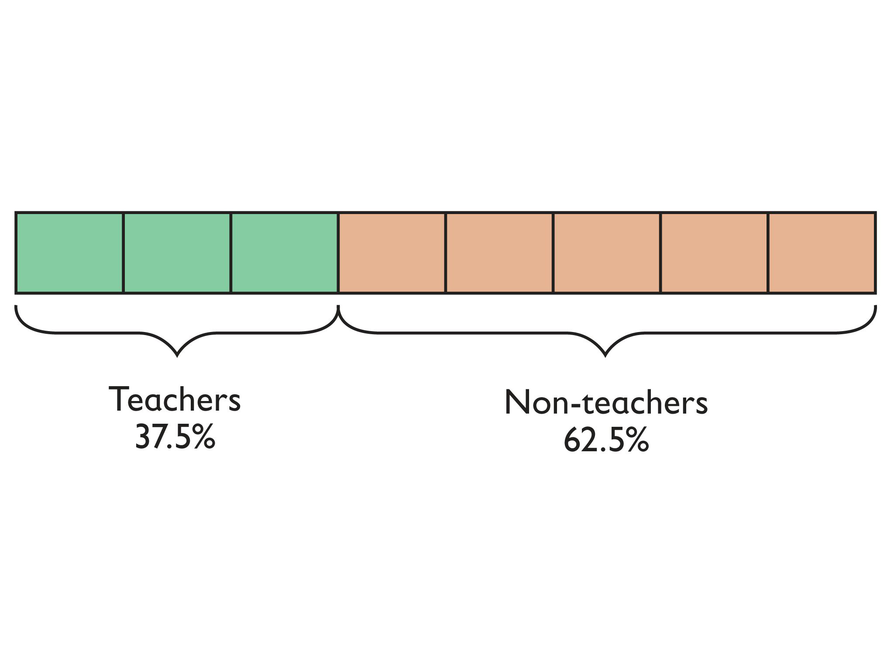
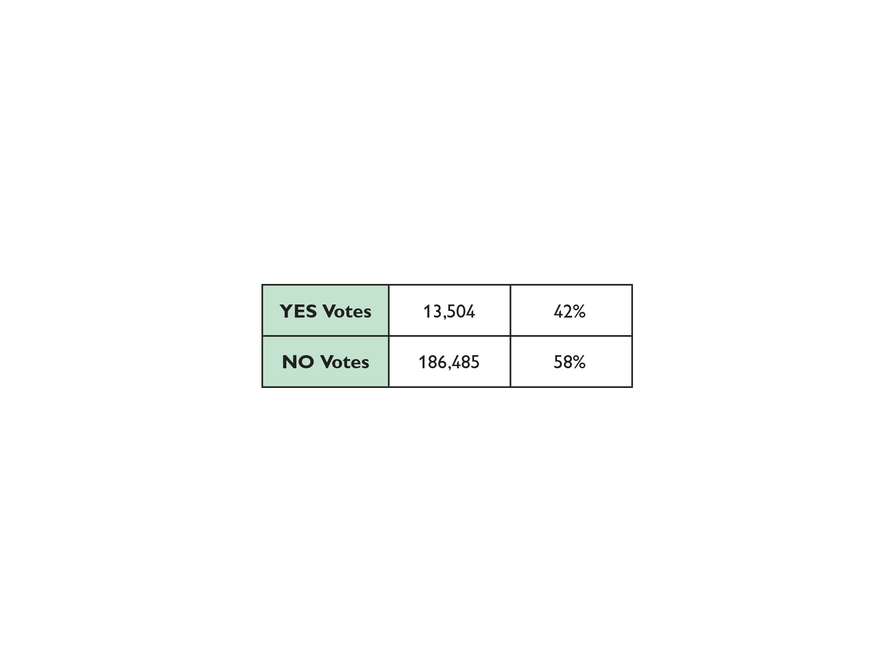
The stadium can host about 111,000 spectators. During one match, there are exactly 110,000 spectators. Of the spectators, 10,000 are women.
One reporter says the ratio of women spectators to total spectators is 10:100, which is exactly 10%.
Another reporter disagrees. He says the ratio 10 women to 100 men is not the same as saying that 10% of all spectators are women.
- Misunderstandings like this happen quite often. Who is right? Explain your reasoning.