Building Bridges
Opening
Work Time
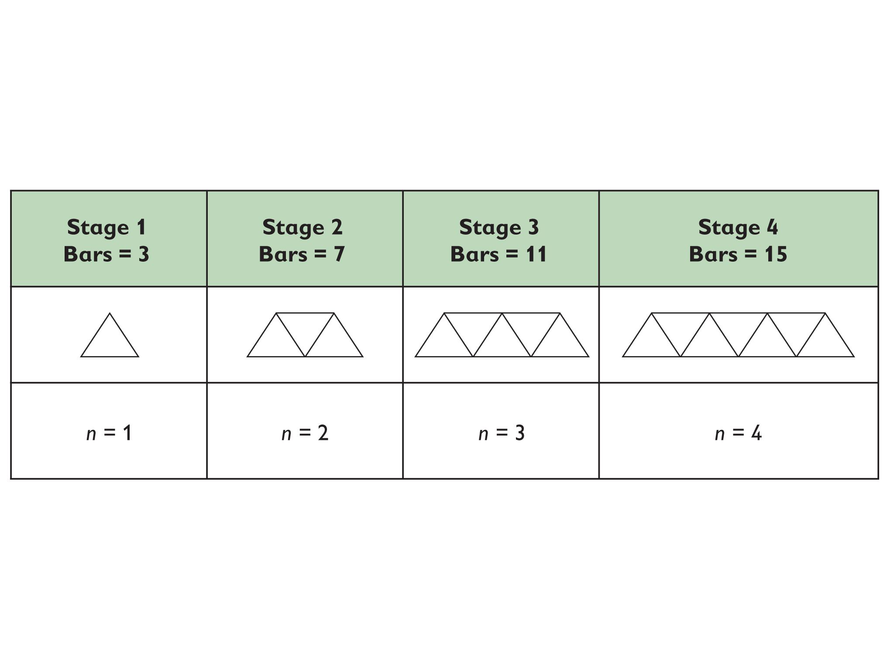
Building Bridges
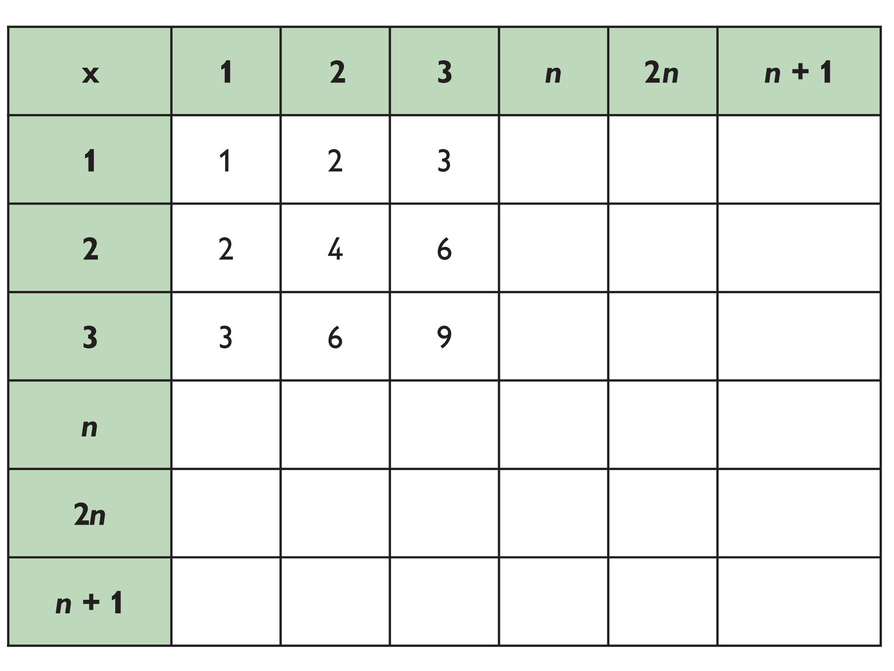
The diagrams in this table represent a series of bridges. The bars are the segments that make up a bridge. n represents the number of triangles. b represents the number of bars.
The following algebraic expressions show different ways to calculate the number of bars based on the number of triangles.
b = 3 + 4(n – 1)
b = 3n + (n – 1)
b = 4n – 1
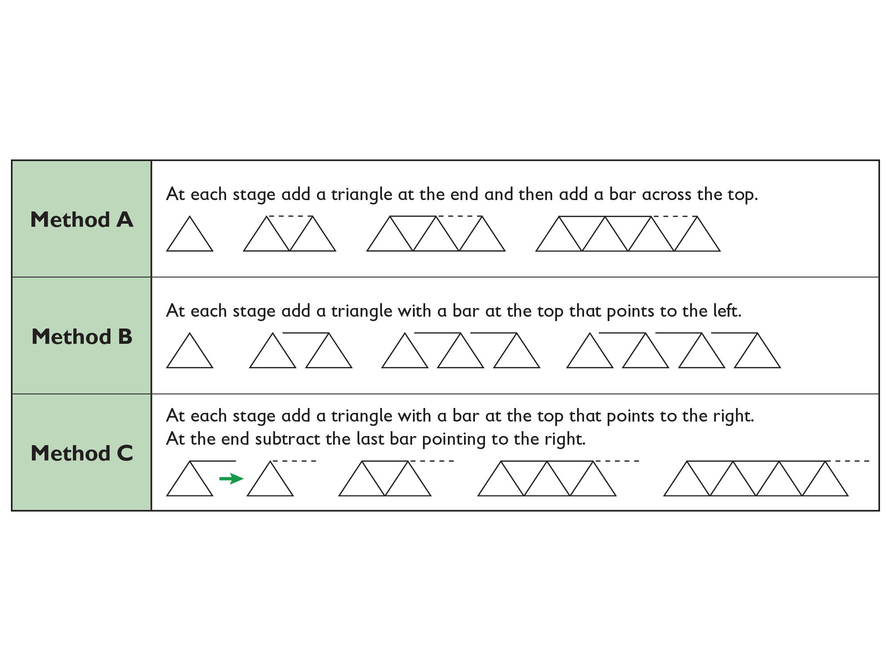
Each expression was found based on a different method for constructing the bridges. These methods are explained and illustrated here.
Method A: At each stage add a triangle at the end and then add a bar across the top.
Method B: At each stage (after the first stage) add a triangle with a bar at the top that points to the left.
Method C: At each stage add a triangle with a bar at the top that points to the right. At the end subtract the last bar pointing to the right.
- Determine which expression matches which method/diagram.
- Evaluate each expression for n = 10.