Dog and Cat
Work Time
Dog and Cat
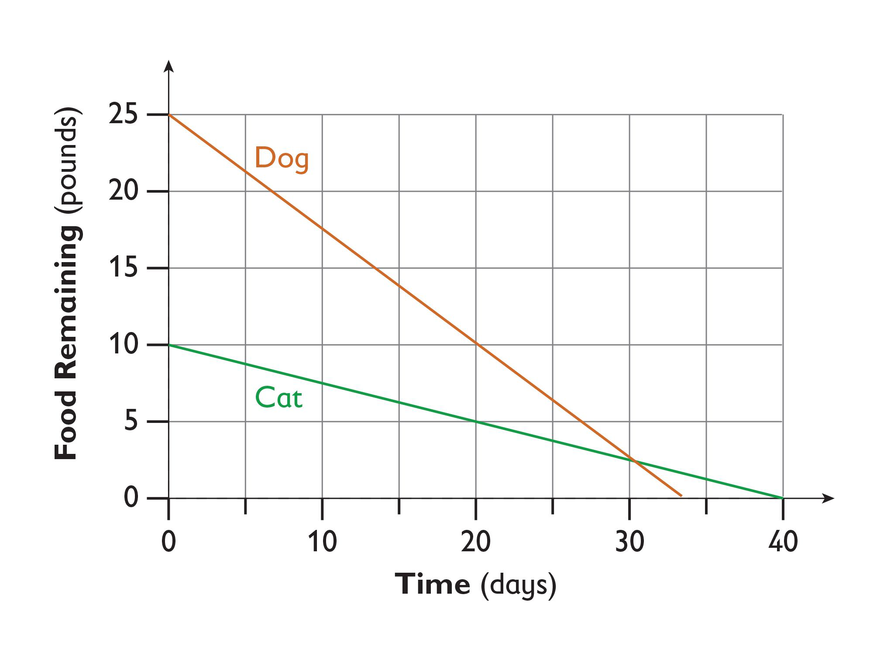
Rosa’s dog eats dry dog food. Rosa’s cat eats dry cat food. Each animal started eating from a new bag of food on the same day. Rosa graphed the situation as shown.
- What information can you conclude from the graph? Be specific.




 VIDEO: Container
VIDEO: Container