Map Reading
Work Time
Map Reading
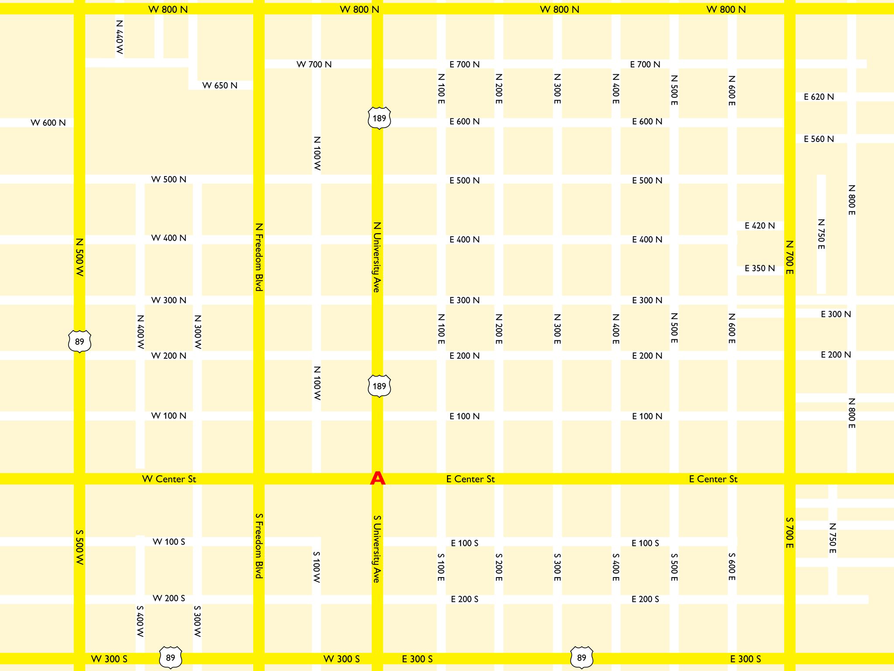
This is a street map of the city of Provo, Utah.
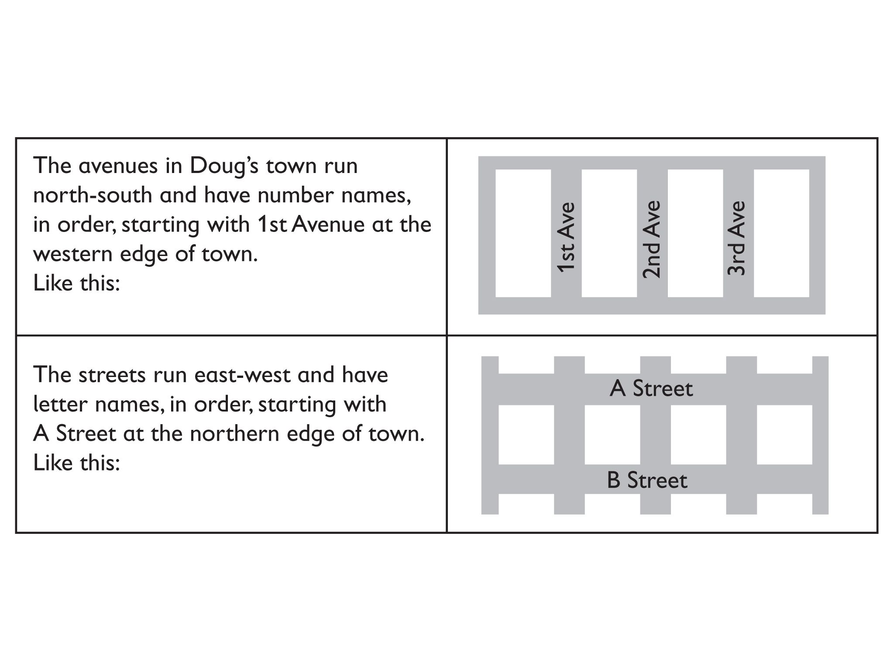
The street map can be thought of as a coordinate system. At the letter "A," you see the center of town, the origin of the street map coordinate system. The street map coordinates that are used here consist of names starting with W, E, N, or S, and number likes 100, 200, 300, etc., that are followed by W, E, N, and S.
- What does W 200 N Street mean? Find the street on the map.
- Imagine placing over the street map an x–y coordinate grid, whose origin is labeled A. The coordinates of the streets are given by the numbers 1, 2, 3, etc. Center Street can be seen as the x-axis, Route 189 as the y-axis.
- Where is the point with coordinates (3, –1)? And (–4, 1)?
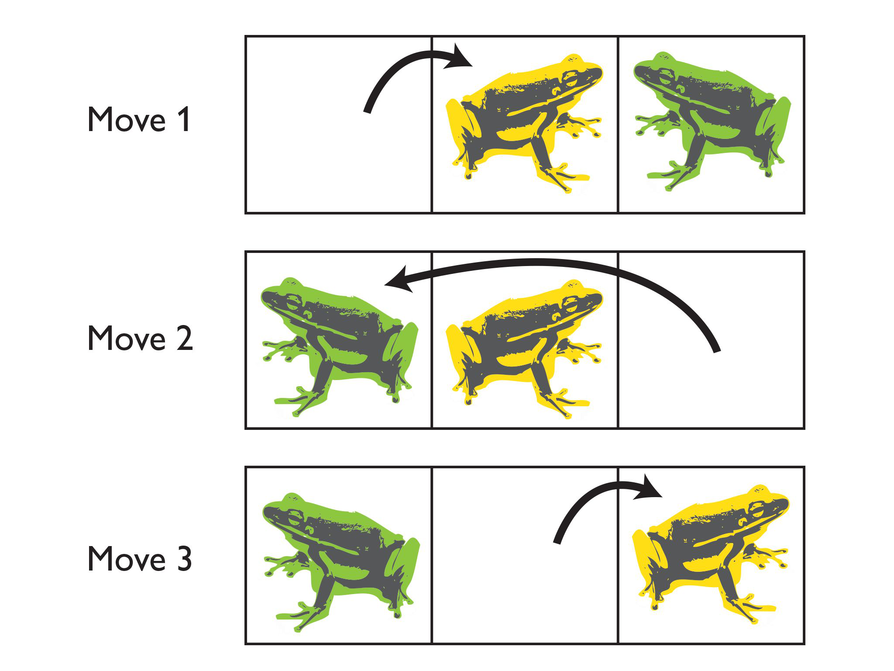
- What is the smallest number of blocks you would need to walk to get from one of these points to the other?
- Create a problem for someone to solve by giving a route based on coordinate clues to find a specific location.
- How can you tell which streets are west of Route 189? What type of integer would you use on the x–y coordinate grid to represent these streets? What coordinate, x or y, represents east-west streets?
- How can you tell which streets are south of Route 89? What type of integer would you use to represent these streets? What coordinate, x or y, represents north-south streets?


 VIDEO: Time-Lapse Birthday Candles
VIDEO: Time-Lapse Birthday Candles