Divide a Paper Into Fourths
Opening
Divide a Paper Into Fourths
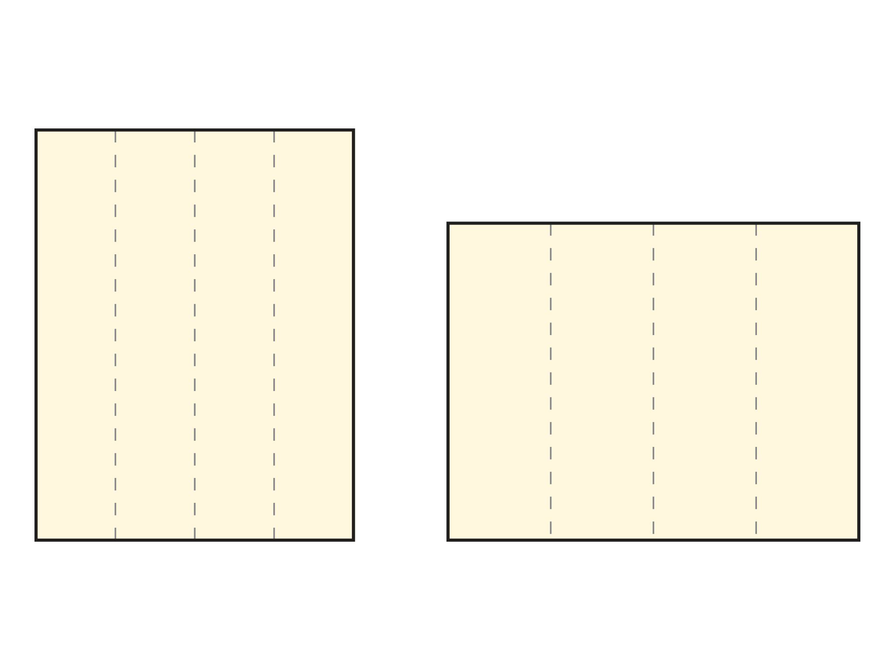
Start with two 8 by 11 in. sheets of paper.
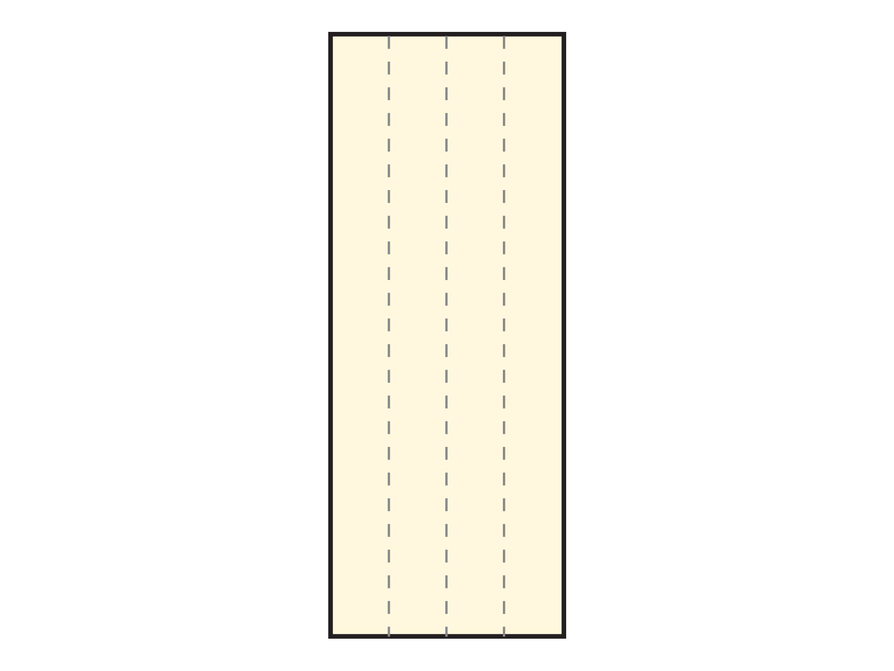
- Using a ruler, divide each sheet into fourths as shown in the diagram.
- Draw lines to mark the divisions.

Start with two 8 by 11 in. sheets of paper.
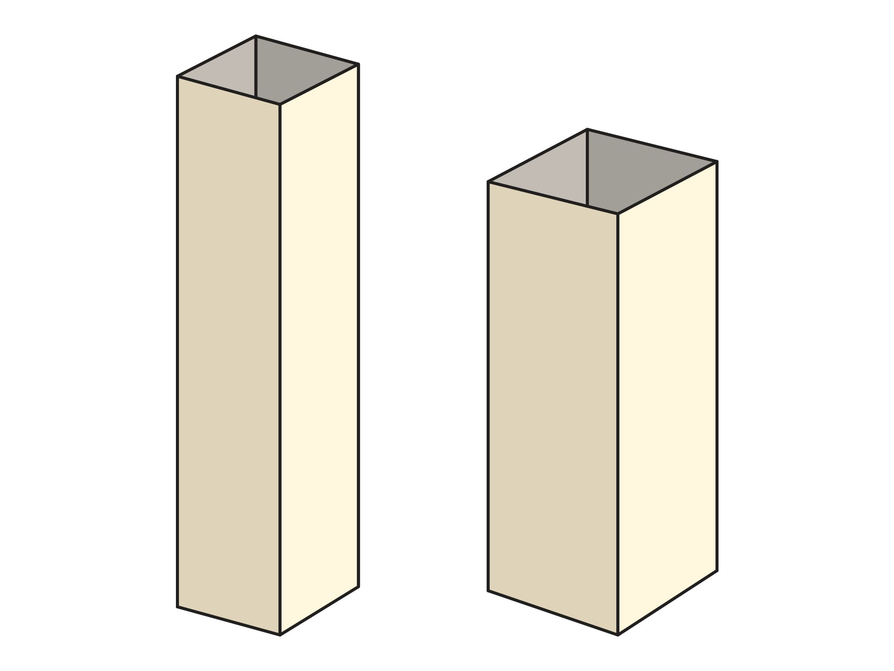
Explore the surface area and volume of prisms.
Think about the four faces (sides) of the two paper prisms.
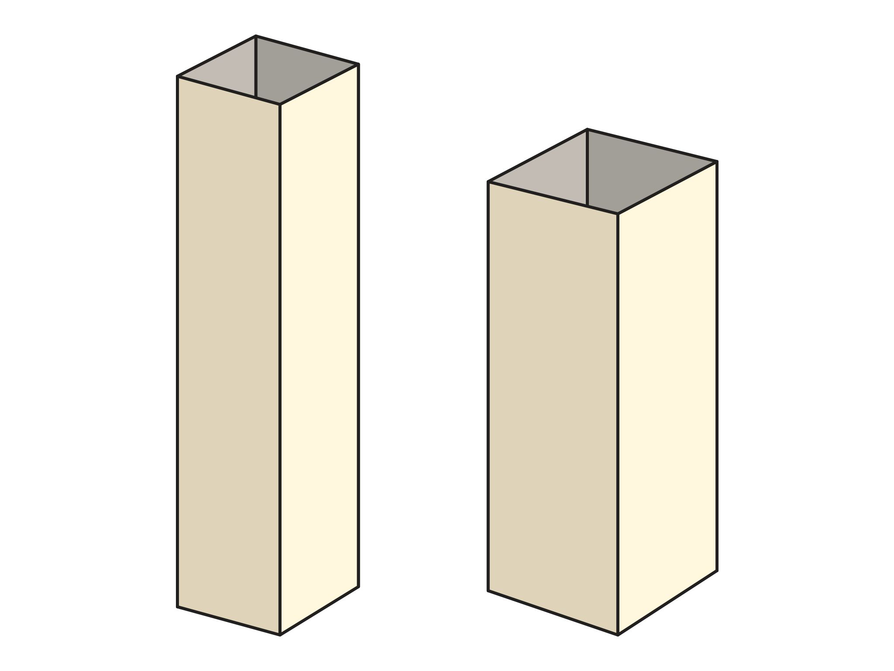
Suppose that you added a top and bottom to each prism.
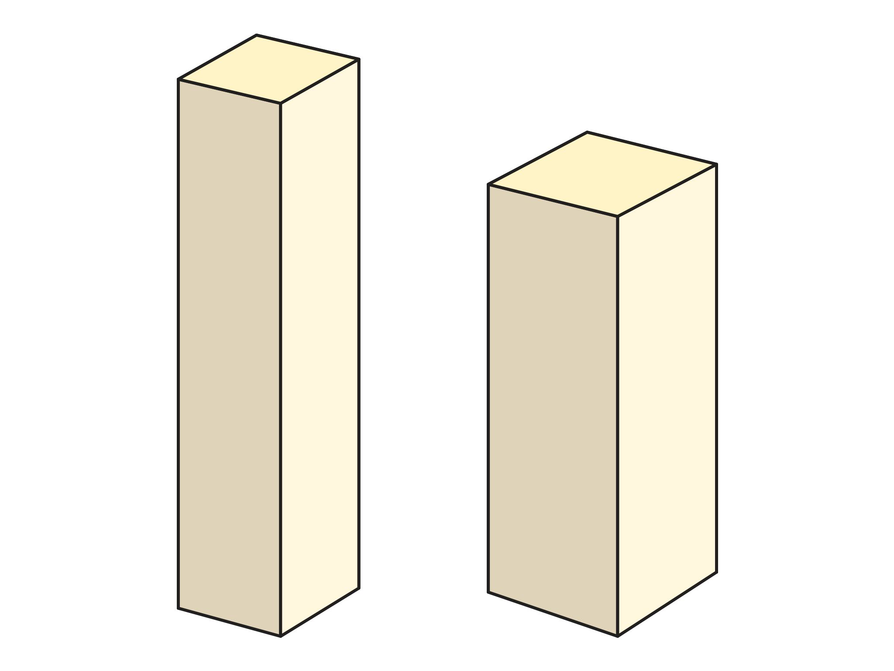
Suppose that you made two other prisms, but this time you started with a half-sheet of paper like the one in the diagram. (The half-sheet measures 4 by 11 inches.) Assume that these prisms have tops and bottoms.
Take notes about your classmates’ thinking concerning the surface areas and volumes of the different prisms.
As your classmates present, ask questions such as:
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about rectangular prisms is …