About Base and Height
Opening
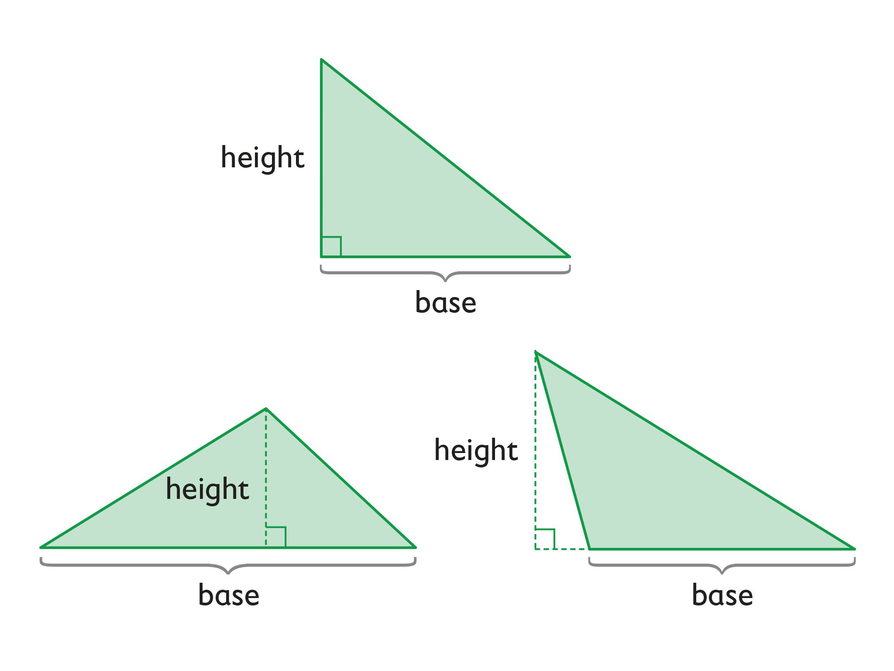
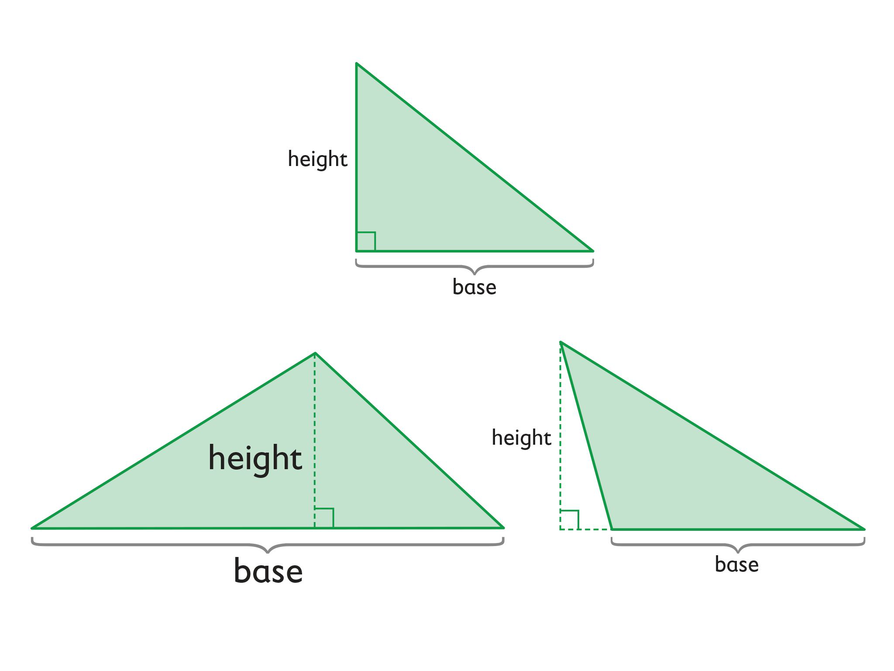
About Base and Height
Discuss the following statements.
- The base of a triangle can be any of the three sides.
- The height of a triangle is the perpendicular distance from the base to the vertex opposite the base.
- As shown in the diagram, the height can be inside or outside the triangle, or it can be one of the sides.