Work Time
From 3-D to 2-D and Back
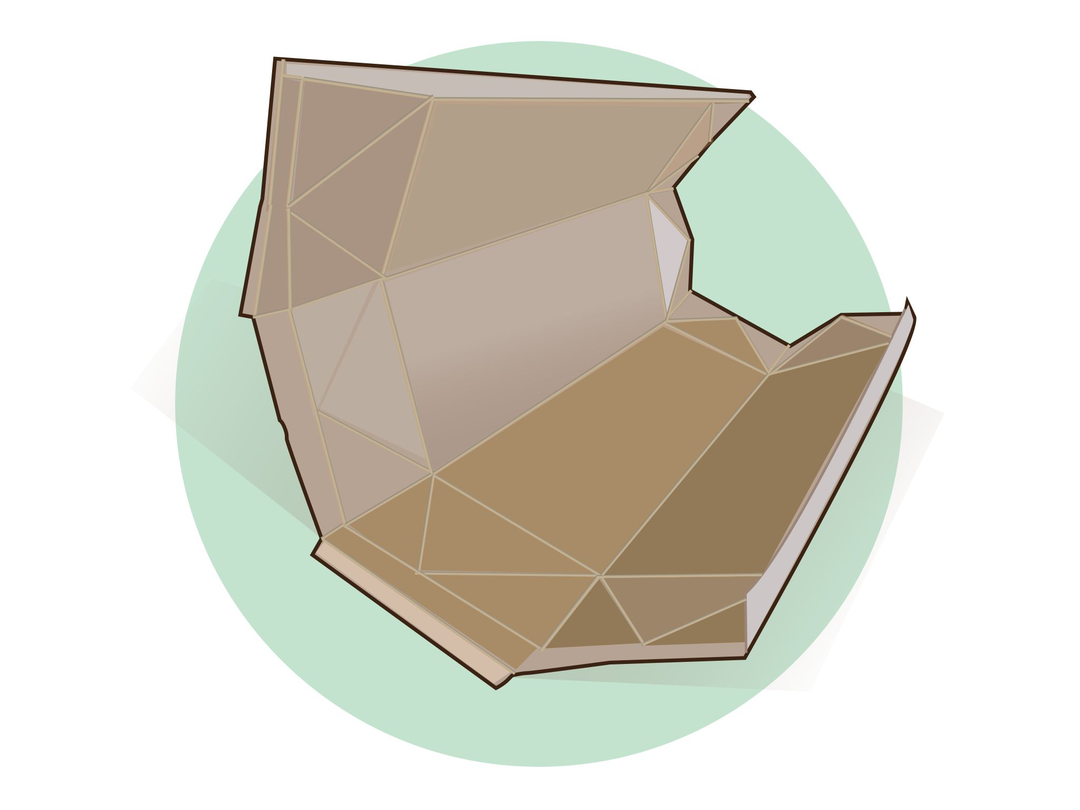
While traveling in the Netherlands, Denzel bought a liter of milk. This image shows what the carton looked like.
This type of carton is constructed to allow a combination of pushing and pulling to make a convenient pour spout.


Denzel cut and unfolded the carton as shown.
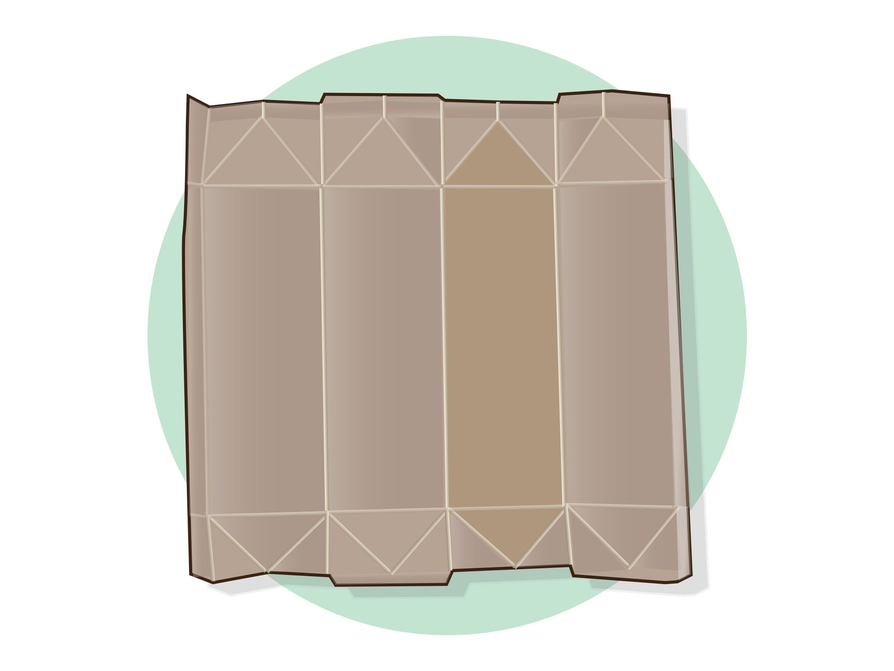
He flattened the carton to get the net shown below.
- The base of the carton is a square with side lengths of 7 centimeters. How high must the carton be to have a volume of 1 liter? (1 liter = 1 cubic decimeter)
- The net for the carton is almost a perfect square with dimensions 29 centimeters by 29 centimeters. The triangles at the top and bottom of the net are what make it possible to transform the square into a milk carton just by folding. Explain why the heights of the triangles that form the top of the carton are taller than the heights of the triangles that form the bottom of the carton.
- The four isosceles triangles at the bottom of the net each have a base length of 7 centimeters and a height of 3.5 centimeters. Draw four isosceles triangles with these dimensions. Cut out the triangles and show that they form a square.
- Explain why four isosceles triangles each with a base length of 7 centimeters and a height of 4 centimeters do not form a square.
- Draw a precise net of a half-liter carton, and build it.