Introduction to the Line Plot
Opening
Introduction to the Line Plot
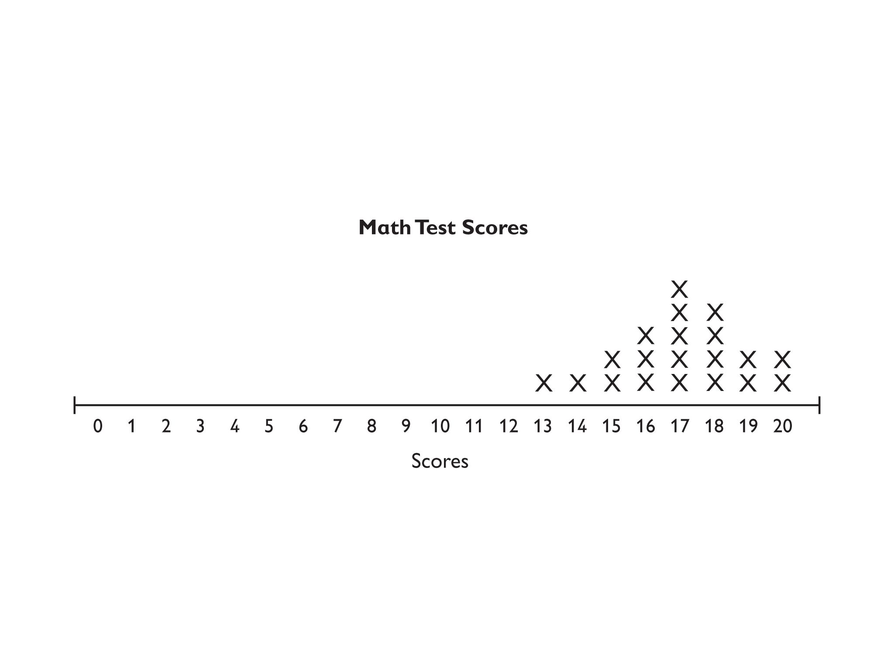
Look at this line plot.
- Without making any calculations, what do you think the mode, median, and mean are for the data shown?

Look at this line plot.
Create line plots that fit given criteria about measures of center.
Explore the line plot.
Start by entering some data. Explain what you did to reach each of the following goals.
(NOTE: To change the starting number, you need to click and drag rather than use you finger.)
INTERACTIVE: Line Plot with Stats
With a partner, continue working with the line plot, and answer the following questions:
INTERACTIVE: Line Plot with Stats
Think about whether the median would go up or down if you added a data point above the median.
Prepare a presentation that explains how you changed the measures of center by adjusting the points on the line plot.
As your classmates present, ask questions such as:
Read and Discuss
Can you:
Write a reflection about the ideas discussed in class today. Use this sentence starter if you find it to be helpful.
When I look at a line plot, this is how I find or estimate the measures of center (mean, median, and mode) and spread (range and outlier) ...