Introduction to Percent
Opening
Introduction to Percent
Discuss:
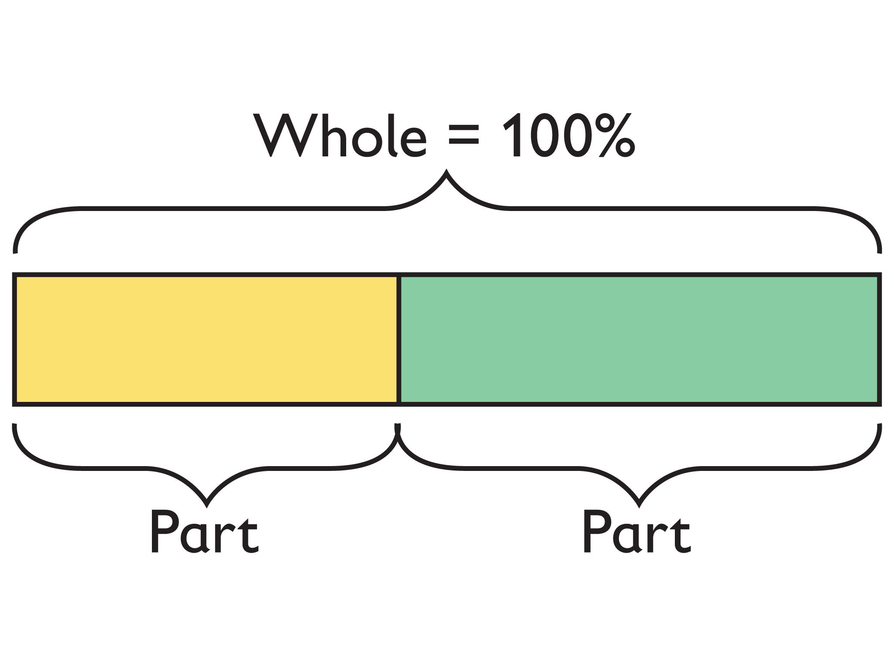
- Most of the relationships you have looked at in this unit are part-part relationships.
- For example, 60 students like action movies, and 40 students do not like action movies. The quantity 60 is one part, and the quantity 40 is the other part.
- You can think about this situation in another way.
- You can say that out of 100 students, 60 students like action movies. You can also say that out of 100 students, 40 students don't like action movies.
In this way of expressing the relationships between the quantities, 60 and 40 are parts and 100 is the whole.
- You can say that out of 100 students, 60 students like action movies. You can also say that out of 100 students, 40 students don't like action movies.