Critique
Opening
Critique
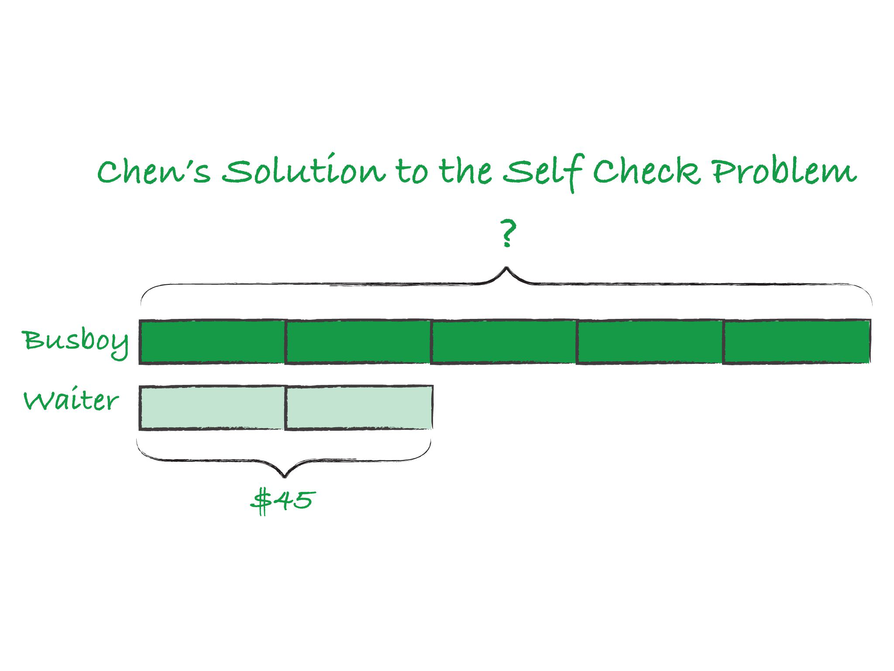
Revise your work on the Self Check problem from the last lesson, based on the following questions.
- Did you identify the quantities in the situation, both known and unknown, and then use a tool to represent how the quantities are related?
- Did you make a conjecture about the amount the waiter gave the busboy? Is this amount less than or greater than $45?
- How can you demonstrate that your answer is correct?
INTERACTIVE: Double Number Line Tool
INTERACTIVE: Ratio Table Tool