Revise and Extend Your Work
Opening
Check Your Understanding
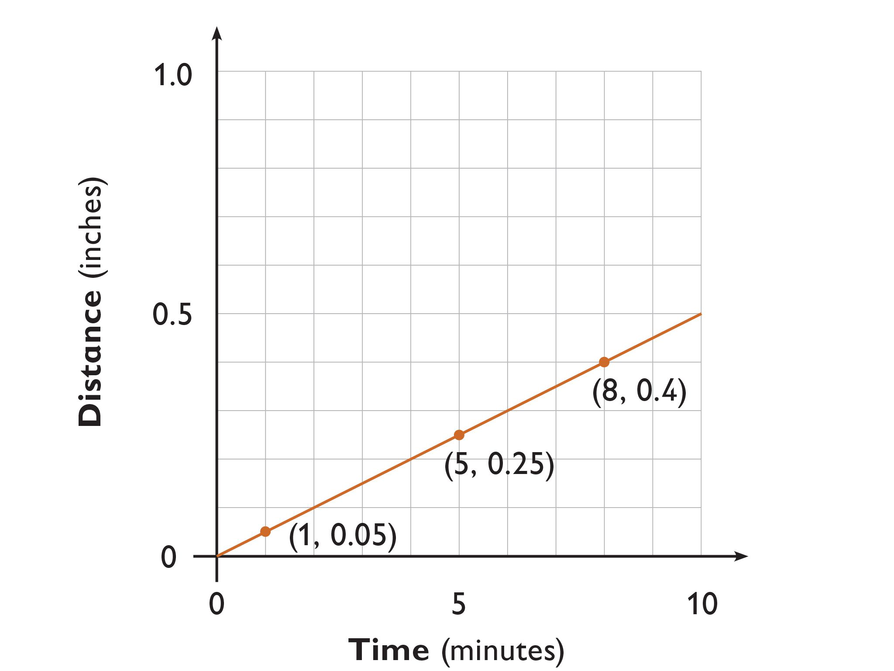
Use the graph to answer the questions.
- Does this graph most likely show the speed of a garden snail or a cheetah?
- How far did this creature travel in 8 minutes?
- How far did this creature travel in 3 minutes?
- What is this creature’s rate of speed in inches per minute?
- Solve an equation to find the distance the creature travels in 12 minutes.
- Solve an equation to find the time it takes the creature to travel 2 inches.