- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Hummingbird
Analyzing Formulas & How Variables Relate

Overview
Students explore the relationship between the flapping frequency, the amplitude, and the cruising speeds of a variety of animals to calculate their Strouhal numbers.
Key Concepts
Students are expected to use the mathematical skills they have acquired in previous lessons or in previous math courses. The lessons in this unit focus on developing and refining problem-solving skills. Students will:
- Try a variety of strategies to approaching different types of problems.
- Devise a problem-solving plan and implement their plan systematically.
- Become aware that problems can be solved in more than one way.
- See the value of approaching problems in a systematic manner.
- Communicate their approaches with precision and articulate why their strategies and solutions are reasonable.
- Make connections between previous learning and real-world problems.
- Create efficacy and confidence in solving challenging problems in a real-world setting.
Goals and Learning Objectives
- Analyze the relationship between the variables in an equation.
- Write formulas to show how variables relate.
- Communicate findings using multiple representations including tables, charts, graphs, and equations.
Hummingbird and Albatross
Lesson Guide
Begin by watching the videos of the hummingbird and the albatross with the class.
Speed versus Size
Lesson Guide
Introduce Vincent Strouhal and the Strouhal number. Tell students that the Strouhal number is calculated by multiplying the wing-flapping frequency by the amplitude and then dividing by the animal's cruising speed. Pose the questions:
- How does the wing-flapping frequency of the hummingbird compare to that of the albatross?
- About how many wing flaps per second do you think the hummingbird and the albatross make when flying at cruising speed?
Give students an opportunity to discuss the answers to these questions with their partners and then share their thinking with the class.
SWD: Go over the mathematical language used throughout the module. Make sure students use that language when discussing the problems.
Mathematics
It is imperative that the students understand the variables involved in this problem including frequency, amplitude, and cruising speed. Ask guiding questions to help students make sense of how these variables are related, for example:
- As the amplitude increases, what would you expect to happen to the frequency? Why?
- How are the frequency and amplitude related to the cruising speed of each bird?
- How does the amplitude affect the cruising speed? What happens to the frequency if a bird with a smaller amplitude has the same cruising speed as a bird with a larger amplitude?
Opening
Speed versus Size
Vincent Strouhal, a physicist from Czechoslovakia, discovered a number that compares the speeds of flying animals with respect to their wing sizes. To calculate the Strouhal number, you multiply the wing flapping frequency by the distance between the tip of the wing at its highest and lowest points, and then divide the result by the animal’s cruising speed.
- How does the wing-flapping frequency of the hummingbird compare to that of the albatross?
- About how many wing flaps per second do you think the hummingbird and the albatross make when flying at cruising speed?
Hummingbird and Albatross
Lesson Guide
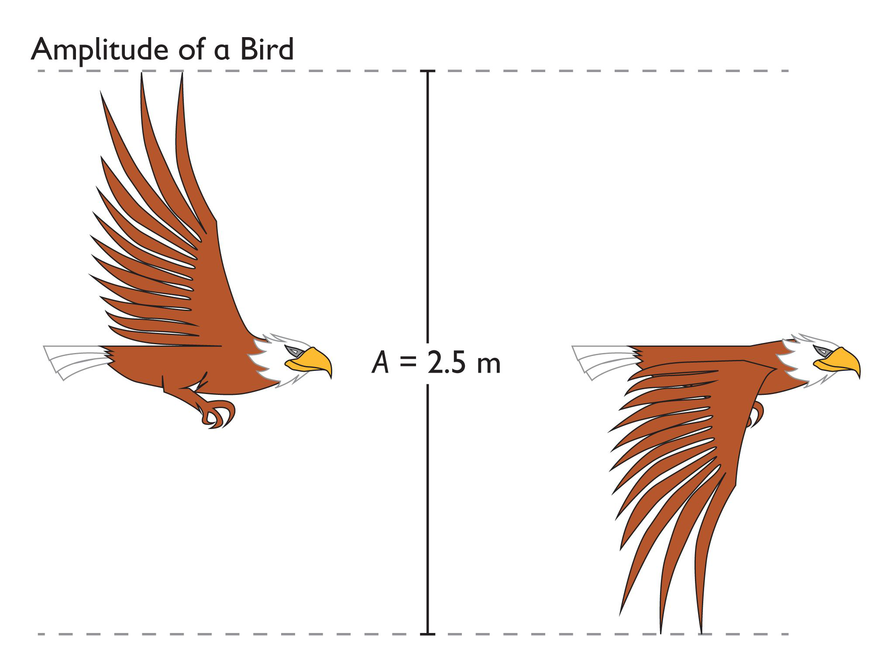
Use the image to demonstrate how the amplitude is calculated for each animal. Give students an opportunity to discuss the answers to these questions with their partners and then share their thinking with the class. Review the amplitude diagram with the students so they know that the amplitude is the distance from the tip of the up stroke to the tip of the down stroke. Pose the question and allow students to discuss their thinking with a partner:
- Do you think the Strouhal numbers for the hummingbird and the albatross are close to each other or far apart?
Opening
Hummingbird and Albatross
The distance between the tip of the wing at its highest and lowest points is called the amplitude. The bird shown below has an amplitude of 2.5 meters.
- How do you think the amplitude of the hummingbird compares to the amplitude of the albatross?
- Do you think the Strouhal numbers for the hummingbird and the albatross are close to each other or far apart?
Problem-Solving Process
Lesson Guide
Before beginning this problem, review the Problem-Solving Steps 1-4 with students. Encourage students to save the problem-solving process to their Notebook to help them review the process.
Problem-Solving Steps
- Understand the problem situation.
- What is the problem asking you to find out?
- What information is provided?
- What are the quantities that vary?
- How are the variables related?
- Represent the situation.
- Write a formula to show how the variables of the Strouhal number relate to each other.
- Answer the question.
- Check that the mathematical answer makes sense.
Opening
Problem-Solving Process
During this unit, you will use the problem-solving process to solve the problems. Review the problem-solving process and discuss with your classmates.
Problem-Solving Process
- Understand the problem situation.
- What is the problem asking you to find out?
- What information is provided?
- What are the quantities that vary?
- How are the variables related?
- Represent the situation.
- Write a formula to show how the variables of the Strouhal number relate to each other.
- Answer the questions.
- Check that the mathematical answer makes sense.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will compare the relative speeds of the hummingbird and the albatross using Strouhal numbers.
Opening
Compare the relative speeds of the hummingbird and the albatross using Strouhal numbers.
Find and Compare Strouhal Numbers
Lesson Guide
Have students work independently on this problem to start. Observe students working, but refrain from asking guiding questions or giving students hints. During independent work time, students are given the opportunity to organize their problem-solving plans and the information given in the problem independently before asking others for assistance. After students work independently, allow students to work with a partner to complete the problems. Have partners share their problem-solving plans. Partners should agree on a plan and work together to find the solutions. During this time, circulate around the classroom asking guiding questions and noting strategies you want students to share during the class discussion.
SWD: Consider the prerequisite skills for this task/skill. Students with disabilities may need direct instruction, review, and guided practice with the skills needed to complete this task.
ELL: When presenting the guiding questions from the Intervention section, be sure that ELLs can follow what you are saying. Provide written questions, use a pace that is appropriate for non-English speakers. Introduce new vocabulary at a slower pace to ensure understanding and recollection of meaning.
SWD: Provide all students who have accommodations, access to a calculator when performing the calculations necessary in this activity.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of the variables involved in this problem (amplitude, frequency, and cruising speed) and use the relationship among the variables to calculate the Strouhal number for each animal. Students must persevere in writing a formula and using this formula to solve the problems.
Mathematical Practice 2: Reason abstractly and quantitatively.
Students use abstract reasoning when describing the relationship among the variables and how a change in one of the variables affects the others. They use their quantitative reasoning skills to represent the problem using formulas and use these formulas to find the solution.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students construct a viable argument stating why they think their mathematical answer is reasonable, and they have the opportunity to critique the reasoning of others during the class discussion.
Mathematical Practice 4: Model with mathematics.
Students may model the situation using tables, graphs, diagrams, and equations.
Mathematical Practice 5: Use appropriate tools strategically.
Students use tools such as calculators and formulas while solving this problem.
Mathematical Practice 6: Attend to precision.
Students attend to precision when calculating the Strouhal number for each of the birds and when making comparisons between Strouhal numbers.
Mathematical Practice 7: Look for and make use of structure.
Students use the problem-solving structure to help them make sense of the problem and obtain a solution.
Interventions
Student has difficulty getting started.
- What are the variables in the problem?
- What information is given to you? What are you trying to find?
- What problem-solving strategies or tools can you use to help you solve the problem?
Student has a solution, but it is incorrect.
- Is your answer reasonable?
- How can you use the relationship among the variables to write the equation?
- Can you make sense of this problem using a diagram?
Student has a solution but is having difficulty articulating his or her thinking.
- How can you describe your thinking to somebody who is struggling?
- How can you state you answer in a complete sentence?
- Does your answer make sense, how do you know?
Student has a correct solution and is waiting on others to finish.
- What other strategies can you use to solve this problem?
- Find the amplitude, frequency, and cruising speed of another bird and have your partner find the Strouhal number of that bird.
- Research Vincent Strouhal.
Answers
The Strouhal number for the hummingbird is about .
The Strouhal number for the albatross is 0.25.
- The two Strouhal numbers are almost the same. The hummingbird has a slightly higher Strouhal number.
Work Time
Find and Compare Strouhal Numbers
To calculate the Strouhal number, you multiply the wing-flap frequency by the distance between the tip of the wing at its highest and lowest points, and then divide the result by the animal’s cruising speed.
Use the data in the table and the problem-solving process to answer these questions.
- What is the Strouhal number for the hummingbird?
- What is the Strouhal number for the albatross?
- How do these two numbers compare?
Begin by writing a formula for calculating the Strouhal number for any bird. To help you write this formula, ask yourself:
- What are the variables in the problem?
- How are the variables related?
- What information about Strouhal numbers is given? How can you use this information?
- What mathematical operations do you need to include in your formula?
Prepare a Presentation
Preparing for Ways of Thinking
As pairs work, identify students who use different strategies and have them share during the class discussion.
Look for students who:
- Organize the information and describe the relationship between the variables in different ways.
- Use graphs or diagrams to find the solution.
Use different ways to manipulate the formula to solve for the cruising speed when given the Strouhal number in the Challenge Problem. For example, some students may rewrite the formula as:
...while others may use the original formula and solve for the unknown variable.
Challenge Problem
Answers
The cruising speed of the Eurasian Kestrel is 8.19375 meters per second.
Work Time
Prepare a Presentation
Prepare a presentation on your findings for Strouhal numbers. Explain how the Strouhal numbers compare to each other. Support your answers with calculations, diagrams, and formulas to explain why your answers make sense.
Challenge Problem
The Strouhal number for the Eurasian Kestrel is 0.24. The bird has an amplitude of 0.345 meters and a wing-flap frequency of 5.7 flaps per second.
- What is its cruising speed?
Make Connections
Mathematics
Highlight the different strategies students used to solve the problems. Focus on how students created and implemented a problem-solving plan. Encourage discussion about the approaches for solving problems and the validity of the answers. Prompt students to give the presenters positive feedback as well as opportunities for improvement. Students should be refining their own strategies, correcting solutions, and taking notes on a workpage during the presentations.
Ask guiding questions, for example:
- How did you approach the problem? What strategies did you use?
- What is the relationship between the amplitude and frequency? How do these affect the cruising speed of the bird?
- Do you think all Strouhal numbers are close? Why or why not?
- How did you manipulate the formula to find the cruising speed when given the Strouhal number, amplitude, and frequency?
- How did you persevere in finding the solution?
- How do you know that your answer is reasonable?
- What tools did you use to help you find your solution?
- What was the most challenging aspect of the problem? How did you overcome this challenge?
- Are there multiple solutions to the problem? Why or why not?
Point out any mathematical processes you observed students using.
Have students who completed the Challenge Problem share their solutions.
ELL: Use a pace that is appropriate for ELLs when posing these questions, especially when using words that students have recently learned. Allow ELLs to use a dictionary if they wish.
Performance Task
Ways of Thinking: Make Connections
Take notes about classmates’ calculations and comparisons of the Strouhal numbers, and other students’ use of the problem-solving process.
As your classmates present, ask questions such as:
- What is the relationship between the variables in the problem? How did you use this relationship to help you write your formula?
- As the wing-flap frequency of a bird increases, what happens to the amplitude? Why?
- Do you think the Strouhal numbers for all birds compare in the same way that the numbers for the hummingbird and the albatross compare? Why or why not?
- Which steps of the problem-solving process were the most helpful when answering the questions?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what surprised students about what they learned.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I learned today that surprised me is…