- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Introducing the Constant of Proportionality
Defining The Constant Of Proportionality

Overview
Lesson Overview
Students calculate the constant of proportionality for a proportional relationship based on a table of values and use it to write a formula that represents the proportional relationship.
Key Concepts
If two quantities are proportional to one another, the relationship between them can be defined by a formula of the form y = kx, where k is the constant ratio of y-values to corresponding x-values. The same relationship can also be defined by the formula , where is now the constant ratio of x-values to y-values.
Goals and Learning Objectives
- Define the constant of proportionality.
- Calculate the constant of proportionality from a table of values.
- Write a formula using the constant of proportionality.
Introduction to the Constant of Proportionality
Lesson Guide
- Have students review the table, which compares the dimensions for the Empire State Building and the miniature building.
- Have students discuss with a partner the question, “What is the constant ratio in the table?”
- As a class, review the definition of constant of proportionality.
- Then examine the process of building a formula for proportional relationships.
SWD: Help students with disabilities build their mathematical vocabulary by continually modeling the use of new terms in the context of classroom work and activities.
ELL: Identifying key words is crucial for students. Spend some time discussing the key vocabulary in this unit.
Teacher Demonstration
Demonstrate for the class how the formula r = 20m is built from the two quantities and the constant of proportionality . Model this process; students must build the formula from the same two quantities and the inverse constant of proportionality later in the lesson.
Mathematics
The start of the lesson presents the definition of constant of proportionality and the process of building a formula to represent a proportional relationship. Point out that students have worked with the constant of proportionality before when they worked with unit rates. The unit rate is the same as the constant of proportionality. Ask students the following:
- Why is a unit rate an example of a constant of proportionality?
- Can you think of the constant of proportionality in this situation as a unit rate? Why or why not?
Opening
Introduction to the Constant of Proportionality
Look at the table you completed comparing the dimensions of the real Empire State Building with those of the miniature building.
- What is the constant ratio in the table?
The constant ratio in a proportional relationship is called the constant of proportionality.
You can use the constant of proportionality to write a formula that represents the relationship between the quantities that vary.
- Let m be the height of the miniature.
- Let r be the height of the real building.
The formula that represents the proportional relationship between the dimensions of the real building and the miniature building is r = 20m.
The 20 in the formula is the constant of proportionality.
The formula for a proportional relationship has the form
y = kx
where k is the constant of proportionality.
INTERACTIVE: Introducting the Constant of Proportionality
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find the constant of proportionality for a proportional relationship based on a table of values and use it to write a formula that represents the proportional relationship.
Opening
For a proportional relationship, find the constant of proportionality based on a table of values, and write a formula.
Height of the Miniature
Lesson Guide
Have students work in pairs on all problems and the presentation.
Mathematics
The relationships in the first two problems each have two constants of proportionality. In the Height of the Miniature problem, students are explicitly told which one to use in their formulas.
ELL: Have students share their observations with each other by working cooperatively. This interaction helps students develop English naturally by interacting with others. This will support students who have difficulties generalizing a formula from the table.
Interventions
Student writes the formula given at the beginning of the lesson (r = 20m).
- Your formula has 20 as the constant of proportionality, but the problem asks for . Can you rewrite your formula?
- You wrote one way of expressing the relationship between m and r, but there is another way to express it.
- You’ve expressed r in terms of m. Can you express m in terms of r?
Student doesn’t fully connect the formulas in this lesson with the tables in the previous lesson.
- Look at the table. What additional pairs of values for m and r (or h and m) could be in the table? Does the formula you’ve written relate those pairs of values accurately?
Student thinks the constant of proportionality is the same either way the formula is written.
- Test your formula with at least two pairs of values from the table. Does it work?
- Write the formula using words instead of letters, and read it aloud to your partner. Does it make sense?
Answer
Work Time
Height of the Miniature
The height of a miniature New York City building is the height of the real building. This describes the relationship between the miniature, 1, to the real building, 20.
Let m be the height of the miniature building.
Let r be the height of the real building.
- How would you write a formula using as the constant of proportionality?

Hint:
After you write your formula, try substituting in some numbers for the variables to check that the formula makes sense.
Driving to the Park
Mathematics
The relationships in the first two problems each have two constants of proportionality. In Driving to the Park, students' approaches will determine which constant to use.
Interventions
Student doesn’t fully connect the formulas in this lesson with the tables in the previous lesson.
- Look at the table. Does the formula you’ve written relate those pairs of values accurately?
Student thinks the constant of proportionality is the same either way the formula is written.
- Test your formula with at least two pairs of values from the table. Does it work?
- Write the formula using words instead of letters, and read it aloud to your partner. Does it make sense?
Answers
- Yes, there is a constant of proportionality.
- and are both constants of proportionality when m represents the distance in miles and h represents the time in hours.
- m = 48.33h, or h = ()m
Work Time
Driving to the Park
Look at the table you completed in the last lesson that shows the relationship between the time Mr. Lee drove and the distance he traveled.
- Is there a constant of proportionality? If not, explain why not.
- If so, give the values of both constants of proportionality.
- If this is a proportional relationship, use one of the values to write a formula that represents the proportional relationship between time and distance traveled.
INTERACTIVE: Driving to the Park
Hint:
First write your formula. Then try substituting numbers for the variables to check that the formula makes sense.
Temperature at the Park
Mathematics
This relationship is not constant.
Answers
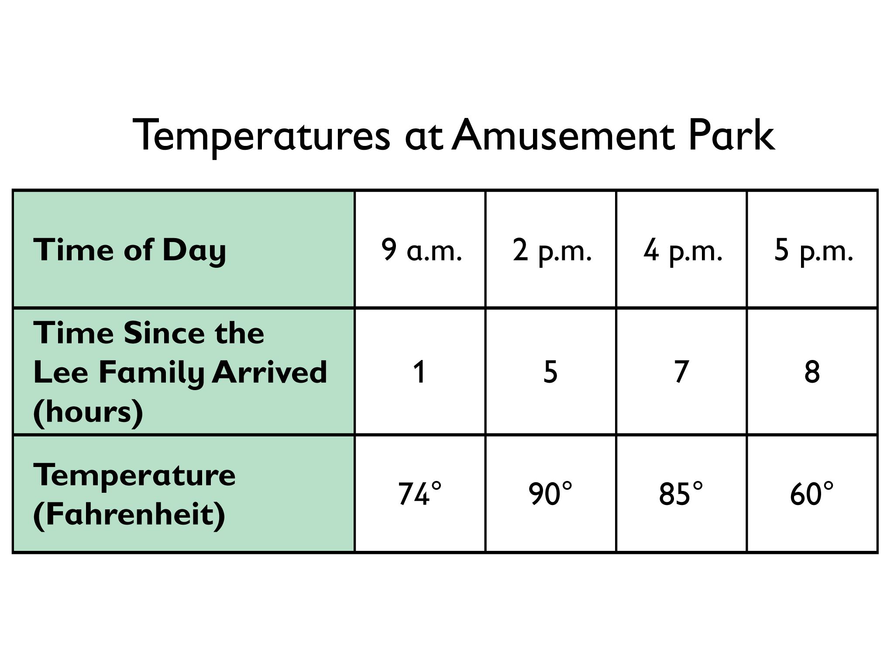
- No, there is no constant of proportionality because the ratio of time to temperature is not constant.
- Since there is no constant of proportionality, there are no values needed.
- No answer needed.
Work Time
Temperature at the Park
Look at the table about the temperature at the amusement park on the day the Lee family visited.
- Is there a constant of proportionality? If not, explain why not.
- If so, give the values of both constants of proportionality.
- If this is a proportional relationship, use one of the values to write a formula that represents the proportional relationship between time and temperature.
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for students who:
- Clearly relate the formulas they write with the tables
- Understand that the formulas express a generalization of what is shown, partially, in the tables
- Connect the formula they write in the first problem with the formula discussed at the beginning of the lesson
- Discuss two possible formulas for the second problem, with different constants of proportionality, and discuss or debate about whether both formulas express the same relationship
- Debate about whether or not there is a constant of proportionality in the third problem
Challenge Problem
Answers
and are both constants of proportionality. Possible explanation: I know because I can rewrite the equation in two ways: x = y and x = y. Both are equivalent to the given equation, and both express the proportional relationship between x and y. The first expresses y in terms of x, and the second expresses x in terms of y. The constant ratio between x and y can be expressed either way—it just depends on which quantity you start with (which might depend on which quantity you have known values for and which quantity you want to find values for).
Work Time
Prepare a Presentation
Explain how you can use a table of values that shows a proportional relationship to help you write a formula that represents the relationship. Justify your thinking with your work.
Challenge Problem
What is the constant of proportionality in this equation? Explain your answer.
Make Connections
Mathematics
Use this part of the lesson to showcase a range of approaches to building a formula from values in a table. Then focus on ways of knowing what the constant of proportionality is in a given proportional relationship and how this constant appears in a formula and a table. Check that students understand—and can correctly use—the term constant of proportionality, recognizing that it is the constant ratio between corresponding values of the quantities that are proportional to one another. Ask the following:
- How is the way [student A] built their formula different from the way [student B] built their formula? How did they use the given information differently? Are their formulas equivalent?
- How does the constant of proportionality show up in each of your formulas?
- Where is the constant of proportionality in the tables?
ELL: As with other discussions, encourage ELLs to use the academic vocabulary they have learned. As they participate in the discussion, be sure to monitor for knowledge of the topic. Make visible important terms that students should use when explaining their understanding around proportional relationships.
Performance Task
Ways of Thinking: Make Connections
As your classmates present, take notes about proportional relationships and the constant of proportionality.
Hint:
As your classmates present, ask questions such as:
- Are there always two ways to write the relationship between two quantities?
- Is there a third way to express the relationship?
- Did you test your formula? How?
- Can you express your formula using words instead of letters? Does it makes sense?
- Where can you find the constant of proportionality in a table?
Proportional Relationships
Lesson Guide
- Have pairs quietly read and then discuss the information shown.
- As student pairs work together, make a note to clarify any misunderstandings in the class discussion.
- After a few minutes, discuss the summary as a class. Ask a volunteer to explain the ratio of tricycle wheels to tricycles and how each equation was written. Then discuss how to calculate the constant of proportionality from a table of values.
SWD: Clearly summarize the lesson and write down all salient information.
Formative Assessment
Summary of the Math: Proportional Relationships
Read and Discuss
The relationship between two varying quantities can be expressed by a constant ratio. For example, the ratio of tricycle wheels to tricycles is 3 : 1.
You can write:
This relationship is an example of a proportional relationship, because even if the total number of tricycle wheels or the total number of tricycles varies, the ratio between the tricycle wheels and the tricycles will remain the same. You say: “The number of wheels is proportional to the number of tricycles.”
You can write: w = 3t
You can also express this relationship as the ratio of tricycles to wheels: the ratio is 1 to 3, or 1 : 3. You say: “The number of tricycles is proportional to the number of wheels.”
You can write: or
Hint:
Can you:
- Write a formula using the constant of proportionality?
- Calculate the constant of proportionality from a table of values?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what still confuses students about the constant of proportionality.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One thing that still confuses me about the constant of proportionality is …