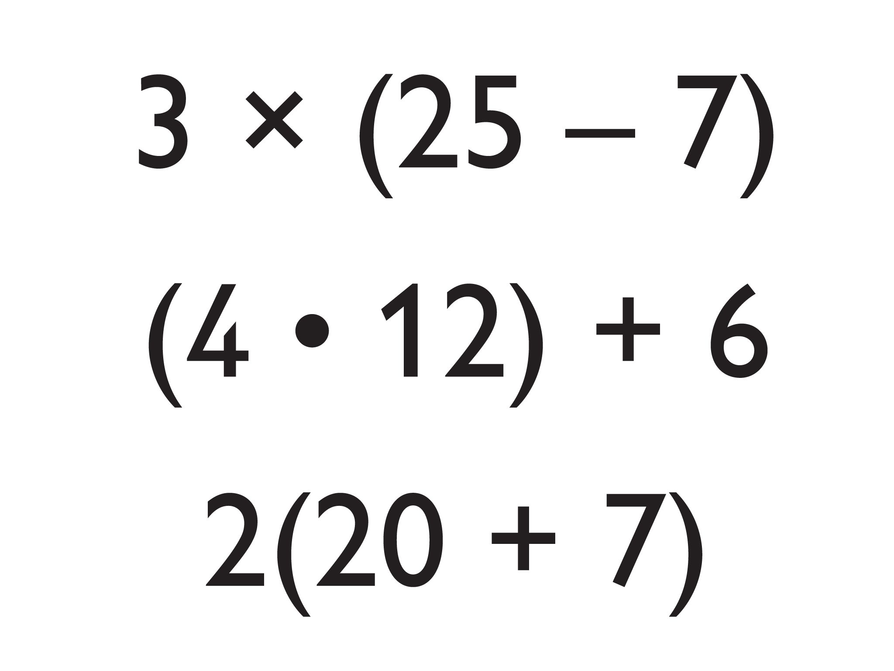Evaluate Expressions

Overview
Students participate in an icebreaker activity, finding a classmate whose card contains an expression equivalent to the expression on their own card. The resulting student pairs will be partners for this unit. Students spend time exploring the digital course. They learn new symbols for multiplication and detect possible errors in evaluating numeric expressions. The class discusses and decides upon norms for math class.
Key Concepts
Students evaluate numerical expressions and identify equivalent expressions. They explore why the order of operations affects calculation results and how to use parentheses to clearly describe the order of the operations.
Goals and Learning Objectives
- Evaluate numerical expressions.
- Understand the reason for the order of operations and how to use parentheses in numerical expressions.
- Use the basic features of the application.
- Create and understand the classroom norms.
- Use mathematical reasoning to justify an answer.
Preparation
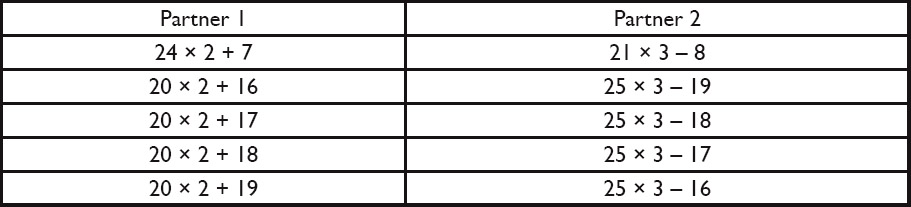
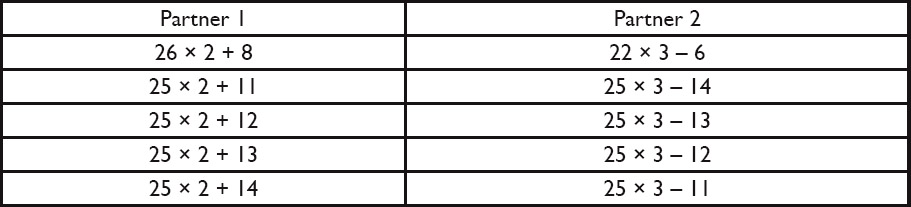
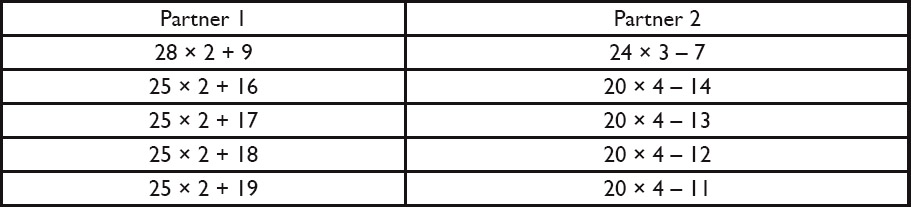
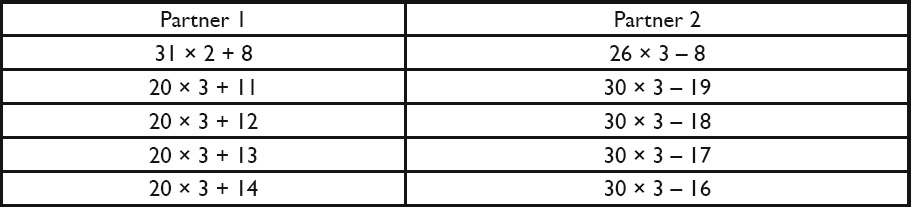
- Print out the Expressions Icebreaker cards. Select the number of pairs of Partner 1 and Partner 2 cards needed for your class. Shuffle the cards before distributing to students.
- Write on the board or chart paper: Find a classmate whose card has an expression that is equivalent to the expression on your card.
- Choose a hand signal or phrase for common activities, such as putting technology away and focusing on the teacher.
Justify Equivalent Expressions
Lesson Guide
Hand out one Expressions Icebreaker card to each student. Tell students to find another classmate who has an expression that is equivalent to the expression on their card. Explain that the two students who have equivalent expressions will be partners.
Once students correctly identify their partners, invite students to explore the digital course together.
Ask students:
- How did you know that your expression was equivalent to your partner’s expression?
Use this discussion to get a sense of students’ ability to explain their reasoning. Do not spend much time correcting reasoning errors at this point.
Students might talk about estimating the result of the expression on their card, identifying expressions that are not equivalent, and the usefulness of evaluating a numerical expression to find an equivalent expression.
For your reference, shown below is the full set of matching cards.
Now, project the Justify Equivalent Expressions image. Explain that students will encounter two new types of multiplication notation this year:
- One type of notation is called a multiplication dot, such as in (4 ⋅ 12) + 6. The dot means the same thing as the multiplication sign, as in 3 × (25 − 7). In this unit, we will also use the letter x to mean “any number.” It can be confusing to see the letter x, which looks similar to the multiplication symbol ×, because the two symbols look similar but have different meanings. Using a multiplication dot can help lessen this confusion.
- In the second type of notation, a number is located directly outside the parentheses and there is no operation symbol between the number and the parentheses, such as in 2(20 + 7). This type of notation means that the number outside the parentheses is multiplied by the total value of the expression inside the parentheses.
If students are confused, clarify; students will see these types of notation throughout the unit.
Have students look at the three expressions in the projected image. Ask students:
- Are these expressions equivalent?
Students should find that all the expressions are equivalent to 54.
Opening
Justify Equivalent Expressions
Discuss:
- How did you know that your expression card was equivalent to your partner’s expression card?
- A multiplication dot or parentheses can be used to represent multiplication.
- Explain why these three expressions are equivalent.
Classroom Norms
Lesson Guide
Explain to students that classroom norms help them to do their best work and meet their learning goals. Today students will spend some time answering these questions as a class:
- What do you need in order to do your best work?
- What ways can you work with your classmates to make the class an effective group?
- What norms, or rules, will allow each member of the class the opportunity to grow?
Have students spend a few minutes thinking about these three questions on their own. Then have students talk about their ideas with their partner. After a few minutes, have students share their ideas with the class. It is best for students to first think of the ideas themselves—they will take more ownership of the ideas as a result. Record students’ ideas for classroom norms.
These Hints for students are ideas for classroom norms:
- Ask questions and think creatively.
- Talk about your ideas and questions with your classmates.
- Use mathematics vocabulary when you talk or write about math.
- Make connections between what you know and what you are learning.
- If you do not know how to solve a problem, write what you do know.
- Think about what you are learning from a task, instead of just trying to finish it quickly.
- Think of a mistake as a chance to learn, not as something to hide.
- Check your work and think about what caused you to make a mistake. Learn how to correct your work.
- Work together with your classmates so that everyone learns.
Tell students about “6 inch voices and sound levels.” This classroom norm means that the volume of students’ voices and technology should travel less than 6 inches. Practice this norm a few times and check with students about how well it is working. This norm is helpful to keep the classroom noise level at an acceptable volume during partner work, especially if students watch Opening videos.
After all ideas about classroom norms are listed, review each idea for clarity and class agreement. Then post the final list for students' reference.
Teacher Demo
To help the class run efficiently, demonstrate your class′s routine for stopping work. For example, show students that clapping your hands is a signal for students to stop their work and focus their attention on you.
Answers
Answers will vary. The class will create their own list of classroom norms together.
Opening
Classroom Norms
Classroom norms help us do our best work and meet our learning goals.
Discuss the following with your classmates.
- What do you need in order to do your best work?
- What ways can you work with your classmates to make the class an effective group?
- What norms, or rules, will allow each member of the class the opportunity to grow?
Here are ideas for classroom norms:
- Ask questions and think creatively.
- Talk about your ideas and questions with your classmates.
- Use mathematics vocabulary when you talk or write about math.
- Make connections between what you know and what you are learning.
- If you do not know how to solve a problem, write down what you do know.
- Think about what you are learning from a task, instead of just trying to finish it quickly.
- Think of a mistake as a chance to learn, not as something to hide.
- Check your work and think about what caused you to make a mistake. Learn how to correct your work.
- Work together with your classmates so that everyone learns.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will detect possible errors while evaluating expressions.
Opening
Detect possible errors while evaluating expressions.
Evaluate Expressions
Lesson Guide
Ask one student to read all parts of the problem aloud. Check that students understand what the problem is asking, but limit the discussion to reading comprehension and language issues.
Have students start working on the problem on their own. After a few minutes, have them check in with their partner to discuss their work.
Interventions
Student thinks the result of the expression is 14.
- What operation do you think the symbol • is referring to?
- The symbols × and • both mean to multiply.
Student has difficulty with the technology.
- Ask (student name) to help you figure out how to use the technology.
Student is confused about how Carlos and Martin could get different answers for the same expression.
- Do you know what it means to evaluate an expression?
- Which operation did Carlos do first to get his answer? What about Martin?
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students think about Carlos’s and Martin’s work and compare the two different approaches to evaluate the same expression. Students identify mistakes to better understand the importance of using parentheses in an expression.
Possible Answers
- Answers will vary. Possible answer: I agree with Martin because the order of operations is to multiply first and then add: 4 ⋅ 2 = 8 and 8 + 8 = 16. Teacher Note: Students might say that they agree with Carlos because he evaluated the expression from left to right: 8 + 4 = 12 and 12 ⋅ 2 = 24. This error shows that students do not understand the rules for the order of operations. If you notice this error, tell students about the convention, but focus on the fact that the expression does not make clear which operation to do first. Students will need to understand how using parentheses in an expression makes it clear which operation to complete first.
- Adding parentheses around 8 + 4 will make Carlos’s equation true: (8 + 4) ⋅ 2 = 12 ⋅ 2 = 24. Adding parentheses around 4 ⋅ 2 will make Martin’s equation true: 8 + (4 ⋅ 2) = 8 + 8 = 16.
Challenge Problem
Answer
- (3 ⋅ 4) + (2 ⋅ 4 ⋅ 8) − 8 = 68
Work Time
Evaluate Expressions
Read the problem and copy it into your notebook.
Carlos and Martin had different results for the same expression.
- Do you agree with Carlos or Martin? Explain your reasons using words and a diagram.
- Add parentheses to Carlos’s and Martin’s work to make both equations true.
Challenge Problem
Add parentheses to this expression so that it has a result of 68.
Hint:
- In what order did Carlos complete the operations to get his result?
- In what order did Martin complete the operations to get his result?
- What are the rules for order of operations?
Reflect On Your Work
Lesson Guide
Explain to students that they will be writing a brief reflection at the end of most classes. They will be given sentences that they can complete or they can write something else about their learning today.
Demonstrate how students will share their work with the teacher. Tell students what they should do with the technology at the end of the lesson and how they should begin the lesson tomorrow.
Review the reflections to see the reasons students find parentheses to be useful.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Parentheses are useful because…