Middle Grades Math 07 Geometry
Middle Grades Math 8 Algebra Part One
Middle Grades Math 8thfinal
The 100 Days of School collection includes Videos, Documents, Interactive, and Media Gallery for Grades PreK-K, K-2, 3-5, 6-8.
Students will explore multi-digit numbers and the relationship between ones, tens and hundreds; a digit in one place is 10x the digit in the place to its right. Students will use their bodies to represent digits in multi-digit numbers up to the hundredths place and compare these numbers using <, =, >. Students will use their bodies as multi-digit numbers to add and subtract.
In this video segment from Cyberchase, the CyberSquad replaces a piece of track to get the Madre Bonita Express to the Mother's Day harvest.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: First pose the question: Here are four triangles. What do all of these triangles have in common? What makes them different from the figures that are no...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * A copy of Grandfather Tang's Story by Ann Tompert * One set of tangrams for each student (see note in commentary) * A set of tangrams for t...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials - 2 clear plastic cups for each pair of students - 4 bean seeds for each pair - soil - unifix cubes - a plant or math journal to record data ...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials A spinner with the numbers 0, 1, 2, ... 9 A spinner with the decades 00, 10, 20, ... 90 Math journal or teacher-made worksheet Pencil Actions...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials For each pair: * 2 ten-sided dice with the numbers 0 to 9 or two spinners with the numbers 0 to 9 * Base-10 blocks, linking cubes, or bundled...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials Set of cards from 1-100, these can be purchased or created using a black marker and index cards Setup Sort the 1-100 cards into sequential gr...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials 20 counters or linking cubes per pair of students pencil copy of the problem Actions The teacher poses the problem: Bo bought 20 tickets to p...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * A cup for each student to represent his/her cave * Counters * Recording sheet Actions The teacher begins by counting out a certain number o...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials A large set of dominoes to affix to a whiteboard or place in a pocket chart, or a regular set to use on a document projector. One set of domi...
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
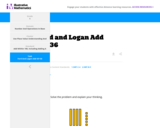
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Materials * Fact Family work sheets * Blank addition and subtraction frames (2 of each) * Numbers cards in fact-family sets Actions As a whole class, t...
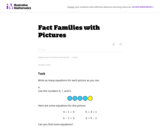
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Write as many equations for each picture as you can. Use the numbers 4, 1, and 5. Here are some equations for this picture. 4+1=5 \hskip4em 5 = 4+1 5-1...