- Author:
- Chris Adcock
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Whole Number Division

Overview
Students explore methods for dividing a whole number by a fraction.
Key Concepts
In earlier grades, students learned to think of a whole number division problem, such as 8 ÷ 4, in terms of two types of equal groups.
Divisor as the Number of Groups
Divide 8 into 4 equal groups and find the size of each group.
Divisor as the Group Size
Divide 8 into groups of 4 and find the number of groups.
To divide a fraction by a whole number in Lesson 2, students used the first interpretation. For example, to find ÷ 4, they divided 8 ninths into 4 equal groups and found that there were 2 ninths in each group.
To divide a whole number by a fraction, the second interpretation is most helpful. For example, to find 3 ÷ , we find the number of groups of 3 fourths in 3 wholes. The diagram in the Opening shows that there are 4 groups, so 3 ÷ = 4.
Just as with whole number division, the quotient when a whole number is divided by a fraction is not always a whole number. Below is a model for 2 ÷ . The model shows that there are 3 groups of 3 fifths in 2 wholes plus of another group ( of a group of 3 fifths is 1 fifth). Therefore, 2 ÷ = 3.
Notice that once we have divided the 2 wholes into fifths, we are finding the number of groups of 3 fifths in 10 fifths. This is simply 10 ÷ 3.
These models can help explain that the “multiply by the reciprocal” method of dividing a whole number by a fraction works. To find 2 ÷
ELL: Encourage students to verbalize their explanations. To help students gain confidence and increase their understanding, allow those that share the same language of origin to speak in small groups using their prefered language.
Goals and Learning Objectives
- Use models and other methods to divide a whole number by a fraction.
Compare Mia’s Methods
Lesson Guide
Give pairs a few minutes to discuss the problem and solution before discussing as a class. Be sure students understand that they are finding the number of fourths in 3, which is 3 ÷ .
Ask students to explain Mia’s solution in their own words. Ask how this problem is different from problems in the previous lesson, which was about dividing fractions by whole numbers.
Opening
Compare Mia’s Methods
Emma runs on a -mile track to train for a marathon. Yesterday Emma ran a total of 3 miles. How many times did she run around the track?
Mia decides to solve this problem using a model similar to the one she used to find in the previous lesson.
She reasons:
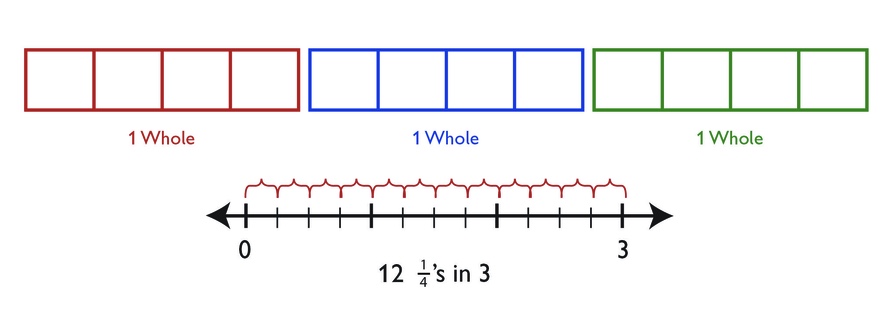
“I need to find the number of miles in 3 miles. So, I need to find 3 ÷ .
“To make a model of this situation, I can draw a bar for each whole mile and then divide each bar into fourths.
“There are 12 fourths in all, so 3 ÷ = 12. Emma ran around the track 12 times.”
- Discuss Mia’s solution. How is her approach similar to the one she used to find ? How is it different?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore strategies for dividing a whole number by a fraction.
Opening
Explore strategies for dividing a whole number by a fraction.
Explore Dividing Whole Numbers by Fractions
Lesson Guide
Students should work in pairs for the Work Time problems.
Interventions
Student has difficulty starting 3 ÷ .
- The model in the Opening shows 3 wholes divided into fourths. How did Mia use this model to help you solve 3 ÷ ?
- In the Opening, you found that there are 12 fourths in 3. Can you use this information to figure out the number of groups of 3 fourths in 3?
SWD: Students with disabilities, especially those with visual spatial difficulties, may struggle to self-assess the accuracy of their drawings. Check in with students to provide coaching as they self-assess their drawings.
Make sure students are creating accurate drawings for dividing a whole number by a fraction.
ELL: When presenting the guiding questions from the Interventions, be sure that ELLs can follow what you are saying. Provide the guiding questions in writing and use a pace that is appropriate for non-English speakers.
Answers
- Diagrams will vary.
- 3 x = = 4. The answer checks.
- Answers will vary. Possible answer: 4 is of the answer to 3 ÷ , which is 12.
- Answers will vary. This makes sense because I am diving the 12 fourths into groups of 3 fourths, which is 3 times larger than 1 fourth.
Work Time
Explore Dividing Whole Numbers by Fractions
Find 3 ÷ .
- Use Mia’s method of using a diagram or a number line.
- Check your answer using multiplication.
- How does your answer compare to Mia’s answer of 12 for 3 ÷ ?
- Given Mia’s answer for 3 ÷ , why does your answer make sense?
- In your model, draw three rectangles to represent the whole number 3. How many equal parts should you divide each rectangle into?
Hint:
- In your model, draw three rectangles to represent the whole number 3. How many equal parts should you divide each rectangle into?
- How can you use your model to show how many three-fourths ( 34 ) are in 3?
Jan’s Method
Mathematics
[common error] Students may be confused about why the quotient is 3 rather than 3, since there is 1 fifth left over. Remind students that they are finding the number of groups of 3 fifths in 2 (or 10 fifths). The 1 fifth that is left over is 13 of a group of 3 fifths.
You might also point out that finding the number of groups of 3 fifths in 10 fifths is the same as finding the number of groups of 3 of any object in 10 objects (e.g., the number of groups of 3 apples in 10 apples). It is just 10 ÷ 3.
Interventions
Student does not understand Jan’s model.
- Why did Jan draw 2 whole bars?
- Why did she divide the bars into fifths?
- What does each shaded group represent? Why did Jan shade these groups?
- How many groups are shaded? How does this relate to the answer?
- How many fifths are left over? How does this relate to the answer?
Answers
- Answers will vary. Possible answer: Jan drew 2 whole bars and divided them into fifths. She wanted to find how many 3 fifths are in 2, so she circled groups of 3 fifths. There were 3 groups and then there was 1 fifth left, which was a third of another group of 3 fifths. This means the answer is 3.
- Answers will vary. Possible answers:
- We are finding the number of groups of 3 fifths in 2. The 1 fifth that is left over is of a group of 3 fifths, so the answer is 3.
- We are finding the number of groups of 3 fifths in 10 fifths. This is the same as 10 ÷ 3, which is 3.
Work Time
Jan’s Method
Jan wants to find 2 ÷ .
She makes the model pictured below. She reasons:
“To find 2 ÷ , I made a model with 2 wholes and divided each whole into fifths. Then I shaded groups of 3 fifths. There are 3 groups of 3 fifths and of a group of 3 fifths left over.
So, 2 ÷ = 3.”
- Discuss Jan’s method with your partner. Then try to explain it in your own words.
- Carlos thinks the answer is 3 because of a whole is left over. Explain why his reasoning is incorrect.
Ask yourself:
- What value does each equal group in the model represent?
- What fraction of an equal group is left over?
Carlos’s Method
Task 5: Carlos’s Method
Mathematics
[common error] Some students, if they use a model instead of multiplying by the inverse, may incorrectly get 4rather than 4 as the quotient in Carlos’s problem because there is 1 third left when 3 (or 9 thirds) is divided into groups of 2 thirds. Point out that this 1 third is half of a group of 2 thirds. Because there are 4 whole groups of 2 thirds and half of another group, the quotient is 4.
You might point out that finding the number of groups of 2 thirds in 9 thirds is the same as finding 9 ÷ 2.
Answers
- 6 ÷ = 15
- The reciprocal of is , so we can rewrite the problem 6 ÷ = 6 · .
Now we can multiply the numerators to solve the problem: 6 · = .
Then simplify the fraction: = 15.
Work Time
Carlos’s Method
Carlos wants to find 3 ÷ . He decides to use the same method he used to find ÷ 4 in the previous lesson: multiply by the reciprocal.
At first, Carlos isn’t sure what to do with . What is the reciprocal of ? He thinks back to a rule he learned: the multiplicative inverse, or reciprocal, of is . For example, the reciprocal of 4 is ; the reciprocal of is 5. So, Carlos determines that the reciprocal of is . He then solves the problem as follows: 3 ÷ = 3 • = .
Thus, 3 ÷ = .
- Use Carlos’s method to find 6 ÷ .
- Describe and explain each step of your solution.
Ask yourself:
Will the answer be greater than or less than 3? How can you use the reciprocal of 25 to solve the problem?
Prepare a Presentation
Preparing for Ways of Thinking
Choose solutions that use a variety of models and methods to be presented during Ways of Thinking. Choose both incorrect and correct solutions. You can use the incorrect solutions to clear up misconceptions students may have.
Select students who correctly solved the Challenge Problem to present during Ways of Thinking. Presentations will vary. They should include an explanation of each problem and a comparison between the three Work Time problems.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students must find ways to make sense of dividing a whole number by a fraction and find a way to represent and solve the given problems.
Mathematical Practice 7: Look for and make use of structure.
- Some students will be able to use structure to help them solve 3 ÷ . From the Opening problem, they know that there are 12 fourths in 3. They may realize that this is 4 groups of 3 fourths, so 3 ÷ = 4. Some students may be able to apply this idea to other problems. For example, to find 3 ÷ , find the number of thirds in 3 and then divide the answer by 2 to find the number of groups of 2 thirds.
Challenge Problem
Answers
3 × 4 ÷ 1 = 12
2 x 5 ÷ 3 = = 3
3 x 3 ÷ 2 = = 4These are the same answers we got using other methods.
- Multiplying the whole number by the denominator finds the number of unit fractions in the whole number (e.g., for 2 ÷ , the number of fifths in 2). Dividing by the numerator divides that total into groups equal to the divisor (e.g., for 2 ÷ , groups of 3 fifths).
Work Time
Prepare a Presentation
- Explain how you solved each problem and why your answer makes sense.
- Explain Jan’s and Carlos’s methods.
Challenge Problem
Denzel uses the following shortcut to divide a whole number by a fraction:
“To divide a whole number by a fraction, I multiply the whole number by the denominator of the fraction, and then divide this product by the numerator of the fraction.”
- Show that Denzel’s method works for the problems from today’s lesson: , , and .
- Why does Denzel’s shortcut work? Explain the mathematics of his method.
Make Connections
Lesson Guide
Encourage students to ask questions during the presentations, especially about Jan’s method.
Mathematics
Denzel’s division method (multiply by the denominator and then divide by the numerator) in the Challenge Problem is a general method students can use to divide a whole number by a fraction without making a model. If no student solved the Challenge Problem, present and explain Denzel’s method yourself.
You can use a specific example, such as 2 ÷ , to explain the method:
There are 2 × 5, or 10 fifths, in 2.
- Multiplying 2 by the denominator, 5, finds the number of fifths in 2.
- Dividing the product, 10, by the numerator, 3, divides the 10 fifths into groups of 3 fifths.
There are 3 groups of 3 fifths in 10 fifths.
You might point out that in the last step, we do not need to think about the fact that the pieces are fifths. We are simply dividing 10 “objects” into groups of 3 “objects,” which means computing 10 ÷ 3. This may help students see why the answer is 3 and not 3.
SWD: Students with disabilities may need additional support in seeing the relationships among problems and strategies. Throughout this unit, keep anchor charts available and visible to assist them in making connections and working toward mastery. Provide explicit think-alouds comparing strategies and making connections. In addition, ask probing questions to get students to articulate how a peer solved the problem or how one strategy or visual representation is connected or related to another.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students must be able to explain the methods presented in the three Work Time problems.
Mathematical Practice 6: Attend to precision.
- Encourage students to use precise language to explain why the methods work. Allow other students to critique the reasoning of presenters and to help clarify confusion and correct misconceptions.
Performance Task
Ways of Thinking: Make Connections
Take notes to clarify your understanding of how to divide a whole number by a fraction.
As your classmates present, ask questions such as:
- How did you use Mia’s solution to 3 ÷ 1 4 to show that your solution to 3 ÷ 3 4 makes sense?
- How is the whole number (the dividend) represented in Jan’s model?
- How is the fraction (the divisor) represented in Jan’s model?
- What does “amount left over” in Jan’s problem mean?
- Why does Carlos’s method work?
Divide Whole Numbers by Fractions
Lesson Guide
Challenge students to use a method that they had not used in the Work Time problems. For students who are fluent in multiple methods, challenge them to create real-world problems. Have students work alone.
Answers
Students' solution methods will vary.
- 5 ÷ = 6
- 6 ÷ = 14
- 8 ÷ = 12
- 5 ÷ = 2
Work Time
Apply the Learning: Divide Whole Numbers by Fractions
Solve the problems using the method of your choice.
- 5 ÷
- 6 ÷
- 8 ÷
- 5 ÷
Divide a Whole Number by a Fraction
A Possible Summary
To divide a whole number by a fraction, you must find the number of times the fraction divides the whole number. One way to find the answer is to draw a model. For example, to find 2 ÷ , you can draw a model of 2 wholes divided into thirds and identify groups of 2 thirds. A shortcut method for finding the answer is to multiply the whole number by the denominator of the fraction and then divide the product by the numerator.
SWD: Scaffold the task of writing a summary into discrete, sequential tasks:
- Identify the big mathematical ideas in the lesson.
- Use a prewriting strategy to organize your thoughts.
- Write a clear, brief explanation of the big ideas in a logical order.
Formative Assessment
Summary of the Math: Divide a Whole Number by a Fraction
Write a summary about how to divide a whole number by a fraction.
Check your summary.
- Do you describe at least one way that you can use a model to divide a whole number by a fraction?
- Do you explain how to use the inverse relationship between multiplication and division to divide a whole number by a fraction?
Reflect On Your Work
Lesson Guide
Have students write a brief reflection before the end of class. Review the reflections to find out what strategies they found useful for dividing whole numbers by fractions.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
A strategy that I found useful for dividing a whole number by a fraction is ….