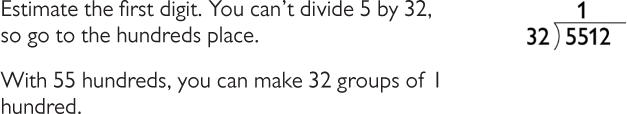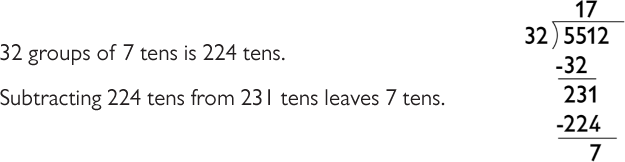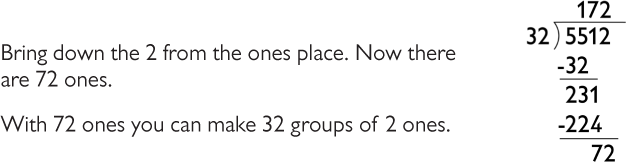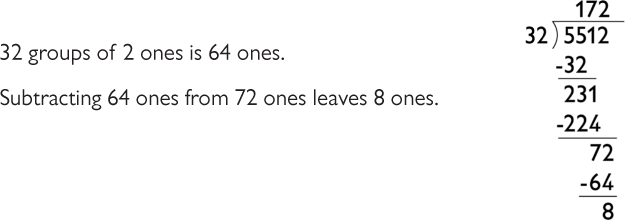The Standard Long-Division Algorithm

Overview
Students review the standard long-division algorithm and discuss the different ways the answer to a whole-number division problem can be expressed (as a whole number plus a remainder, as a mixed number, or as a decimal).
Students solve a series of real-world problems that require the same whole number division operation, but have different answers because of how the remainder is interpreted.
Key Concepts
Students have been dividing multidigit whole numbers since Grade 4. By the end of Grade 6, they are expected to be fluent with the standard long-division algorithm. In this lesson, this algorithm is reviewed along with the various ways of expressing the answer to a long division problem. Students will have more opportunities to practice the algorithm in the Exercises.
Goals and Learning Objectives
- Review and practice the standard long-division algorithm.
- Answer a real-world word problem that involves division in a way that makes sense in the context of the problem.
Compare Solutions
Lesson Guide
Give students a few minutes to discuss the question with a partner; then have students share their ideas with the class.
SWD: Consider the prerequisite skills for this lesson. Students with disabilities may need review, direct instruction, and guided practice with the skills needed to complete the tasks that follow. Make sure all students understand how to divide multidigit whole numbers. If students are unclear, pull a small group and pre-teach the students who are unsure.
Mathematics
Review how the standard algorithm is used to find the quotient in the opening. You might ask students to tell you what to do at each step.
Jason, Denzel, and Martin are all correct. Here is how 172 R8 is equivalent to 172 and 172.25:
- The answer 172 R8 means that when we divide 5,512 into 32 groups, we get groups of 172 with 8 left over.
- If we divide the leftover 8 into 32 groups, there will be another , or , in each group. So, the quotient is 172, (172 + ), or 172.25.
Opening
Compare Solutions
Jason, Denzel, and Martin solved the division problem 5,512 ÷ 32.
All three students started out using the steps shown, but all three got different answers.
Here are their answers:
Jason’s answer: 172 R8
Denzel’s answer: 172
Martin’s answer: 172.25
- Which answer is correct, and why?
- Discuss this question with your partner, and then with your class.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will solve real-world problems by dividing whole numbers.
Opening
Solve real-world problems by dividing whole numbers.
Solve Real-World Division Problems
Lesson Guide
Have students work individually. They should choose just one problem to work on. Make sure that there are students working on each of the four problems so that they can all be discussed in Ways of Thinking.
Mathematics
If students are struggling with the division algorithm, you might walk through the solution with them step by step.
Students should check that the answers are reasonable and make sense in the contexts of the problems. Each problem in this task involves the same division, but the answers differ depending on the situation. Students need to consider whether their answer should be a whole number, a mixed number, or a decimal. If the answer is a whole number, do they need to drop the remainder or round to the next whole number? Is the remainder the answer?
Encourage students to check their answers using estimation or multiplication.
Select students to present so that all four problems are represented. Look for students who offer clear explanations and whose reasoning takes into consideration the problem contexts.
Interventions
Student has trouble understanding how the answer should be reported.
- You are dividing an amount of money. Does it make sense to give the answer as a whole number plus a remainder? In what form are money amounts usually given?
- What does the remainder mean in this situation? Can the student council buy a part of a sweatshirt?
- What does the remainder mean in this situation? Where will the “leftover” campers sleep?
- What do the whole number and the remainder represent in this situation? What is the answer to the question that is asked?
Student gets an incorrect solution.
- Can you use estimation to check your answer?
- Go back and read the problem again. Does your answer make sense in the situation?
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must consider the problems carefully to determine what they are being asked and to devise a strategy for finding it. The context of the problem determines how the answer should be reported. Students need to consider whether the answer should be a whole number, a decimal, or a mixed number. In the fourth problem, they need to understand why the answer is the remainder.
Mathematical Practice 4: Model with mathematics.
The problems illustrate how we can model real-world problems with mathematical expressions. The Challenge Problem asks students to create their own models for the real world.
Answers
All the problems involve the same mathematical expression, 693 ÷ 12, but they have different answers.
- Each person pays $57.75.
- The student council can buy 57 sweatshirts.
- The summer camp needs 58 cabins.
- The employee gets to keep 9 scones.
Work Time
Solve Real-World Division Problems
Choose one of the following problems. Solve the problem and show your work.
- Twelve friends went on a camping trip. The total cost for the campsite, food, supplies, and gas was $693. If the friends split the cost evenly, how much did each person pay?
- The student council is planning a school sweatshirt sale. The council members found a supplier who charges $12 per sweatshirt, but they have to pay the money up front. If they have $693, how many sweatshirts can they buy?
- Each cabin at a summer camp can hold 12 campers. If 693 students sign up for the camp, how many cabins will be needed?
- An employee at a bakery packaged 693 scones in boxes that each hold 12 scones. Her boss told her that she could keep any extra scones for herself. How many scones did the employee get to keep?
Ask yourself:
- Camping Trip Problem: How can you represent the amount left over in this situation?
- Sweatshirt Problem: Can you buy a fraction of a sweatshirt?
- Cabin Problem: Where will the “leftover” campers sleep?
- Bakery Problem: Will the answer be the number of boxes the employee packed or the number of scones left over?
Prepare a Presentation
Preparing for Ways of Thinking
Select students to present so that all four problems are presented. Look for students whose reasoning takes into consideration the problem contexts and whose explanations are clear.
Choose some students to present the problems they created for the Challenge Problem as well.
Challenge Problem
Answers
- Problems will vary.
Work Time
Prepare a Presentation
- Prepare your problem solution to share with your classmates.
- Include a drawing and an explanation of what you did to solve the problem.
Challenge Problem
- Write two word problems that you would solve using the same whole-number division expression, but that have different solutions.
Make Connections
Mathematics
Discuss both incorrect and correct solutions. For each problem, prompt students to consider these questions:
- How can you tell whether the answer will be a whole number, a decimal, or a fraction?
- What does the whole number quotient mean in this situation? What does the remainder mean?
For the Camping Trip problem, if a student got the decimal answer by adding a decimal point and a 0 to the dividend and continuing to divide, be sure to discuss that solution method.
If time allows, ask students to present the word problems they wrote for the Challenge Problem. If several students completed the Challenge Problem, you might create a bank of their word problems and ask other students to each choose two problems to solve as part of the Exercises.
ELL: Create an anchor chart with the word problems. As students present their solutions, illustrate on the chart each of the possible ways to represent the solution. If possible, use pictures and make connections between the different solutions. Students should see that there are multiple ways to represent a solution. Display this anchor chart in a prominent location in your classroom as a visual representation of learning that can be referenced in future lessons. Students will use the anchor chart to approach future problems in a more efficient way.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ approaches to solving the problems.
As your classmates present, ask questions such as:
- Explain each step in your long division procedure.
- Is your answer reasonable? How do you know?
- How does your answer make sense in the context of the problem situation?
- What do the whole number and the remainder each represent in this situation?
Divide Whole Numbers
A Possible Summary
You can use the long-division algorithm to divide two whole numbers. If the divisor does not divide evenly into the dividend, then the answer can be expressed as a whole number and a remainder, as a decimal, or as a mixed number. For example, the answer to 125 ÷ 10 can be written as 12 R5, 12.5, or 12.
When solving a real-world problem involving whole-number division, it is important to consider the context. In some situations, like those involving money or measurements, a decimal answer makes the most sense. Sometimes a mixed number is the best answer. When a whole-number answer makes the most sense, you need to decide whether to drop the remainder or to round it up. In some situations, the remainder is the answer.
Formative Assessment
Summary of the Math: Divide Whole Numbers
Write a summary about dividing with whole numbers.
Check your summary.
- Do you explain how to represent problem situations with whole-number division expressions, and include examples?
- Do you describe and provide examples of the different forms that the answer to a whole-number division problem can have?
- Do you discuss why different problem situations can be represented by the same division expression, and have different solutions?
Reflect On Your Work
Lesson Guide
Have students write a brief reflection before the end of class. Review the reflections to find out their understanding of how mathematics connects to everyday situations.
ELL: Assess students' understanding of dividing multidigit whole numbers and representing their solutions from word problems in various forms (whole number and remainder, decimal, and fraction). Provide students with ample processing time and time to discuss their thoughts with a peer.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Two everyday situations that involve dividing whole numbers are …