- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Lightning and Thunder
Fundamental Problem Solving Concepts

Overview
Students work in a whole-class setting, independently, and with partners to design and implement a problem-solving plan based on the mathematical concepts of rates and multiple representations (e.g., tables, equations, and graphs). They analyze a rule of thumb and use this relationship to calculate the distance in miles from a viewer's vantage point to lightning.
Key Concepts
Throughout this unit, students are encouraged to apply the mathematical concepts they have learned over the course of this year to new settings. Help students develop and refine these problem-solving skills:
- Creating a problem-solving plan and implementing the plan systematically
- Persevering through challenging problems to find solutions
- Recalling prior knowledge and applying that knowledge to new situations
- Making connections between previous learning and real-world problems
- Communicating their approaches with precision and articulating why their strategies and solutions are reasonable
- Creating efficacy and confidence in solving challenging problems in the real world
Goals and Learning Objectives
- Create and implement a problem-solving plan.
- Organize and interpret data presented in a problem situation.
- Analyze the relationship between two variables.
- Create a rate table to organize data and make predictions.
- Apply the relationship between the variables to write a mathematical formula and use the formula to solve problems.
- Create a graph to display proportional relationships, and use this graph to make predictions.
- Articulate strategies, thought processes, and approaches to solving a problem, and defend why the solution is reasonable.
Lightning and Thunder Video
Lesson Guide
Have students watch the video.
The purpose of the Opening is to elicit classroom conversation, pique students' interest in the problem situation, spark students' prior knowledge regarding the mathematics or the subject, prepare students' minds for the type of thinking that will need to occur during the problem, and communicate the mathematical goals of the day. Focus your energy on inspiring meaningful conversation to motivate students to become engaged in the task.
Mathematics
After watching the video of lightning, discuss how to calculate the distance from the viewer's vantage point to the lightning.
Ask students the following:
- How far away is the lightning? What is a good estimate of the distance? What information did you use to make your estimate?
- What additional information would you need to find the actual distance?
Focus on engaging students in the context of the problem more than on the specific mathematics involved. Use the Work Time and the Ways of Thinking portion of the lesson to focus on the mathematical strategies that students used.
Opening
Lightning and Thunder Video
Watch the video.
- Estimate how many miles away the lightning is.
- What would you have to know to find out how far away the lightning is?
VIDEO: Lightning and Thunder
Math Mission
Lesson Guide
Discuss the Math Mission. Students will analyze a simple rule for determining how many miles away lightning is.
Opening
Analyze the following problem: "How many miles away is the lightning?"
Represent the Situation
Lesson Guide
Have students work independently for 3–5 minutes to represent the situation using easy numbers. Then give students 10–15 minutes to work with a partner to make a general representation of the situation that will work for any numbers.
ELL: For ELL students, explaining the meaning of key words such as variable is critical, since they are learning a new language as well as new mathematics. Also consider demonstrating the rule of counting the time between the lightning and the thunder. ELLs may find it easier to understand the rule if they see it modeled.
Mathematics
During the solo time, refrain from giving the students hints, pointers, or asking guiding questions. Encourage students to develop their own unique way of representing the situation using easy numbers. If most of the class is struggling with the topic, give a a few hints to the entire class:
- How can you use ratios to organize the data?
- How can you use an equation?
- How can you use a graph?
As students work together to make a general representation of the situation that will work for any numbers, monitor students for understanding by asking probing questions:
- What information does your ratio table tell you?
- What does the variable represent in your equation? What does this number mean?
- On your graph, what do the labels on the x-axis and y-axis mean?
- How is the data in your table represented in the graph?
- How is the formula related to your table and graph?
- Explain how this [model] represents the problem situation.
Answers
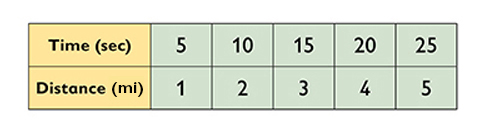
- The lightning is 1 mile away if there are 5 seconds between the lightning and the sound of the thunder.
- The lightning is 2 miles away if there are 10 seconds between the lightning and the sound of the thunder.
Work Time
Represent the Situation
The next step in analyzing the problem is to represent the situation. One approach is to first try to represent the situation using easy numbers.
- How far away is the lightning if there are 5 seconds between the lightning and the sound of the thunder?
- How far away is the lightning if there are 10 seconds between the lightning and the sound of the thunder?
Understand the Situation
Lesson Guide
This Work Time will include solo time, group time, and whole-class instruction to set the tone for the problem-solving unit. It is essential for students to articulate their thought processes while creating their problem-solving plan and for you to highlight these processes to build student confidence and understanding.
Mathematics
Discuss the essential steps in creating and implementing a problem-solving plan:
- Understand the situation.
- Represent the situation.
- Answer questions about the situation.
- Check that your answer makes sense.
- Prepare a presentation.
- Use your analysis to solve other problems.
An important first step is to understand the problem situation. As a whole class, answer the questions in Understand the Situation. Encourage students to ask themselves similar questions when they begin any problem. Often times, students who struggle with a problem in the beginning are not identifying and organizing the information given in the problem situation.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of the given relationship between the sound of the thunder and the distance of the lightning to solve the problem.
Mathematical Practice 2: Reason abstractly and quantitatively.
Students will use an equation to represent the given situation (involving thunder and the distance of lightning) symbolically. They will then use the context of the situation to determine the meaning of the quantities involved.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students will construct a viable argument as they prepare their presentation and defend why their answer makes sense. They will have the opportunity to critique the reasoning of the presenters to help clarify confusion and correct misconceptions.
Mathematical Practice 4: Model with mathematics.
Students will model the situation through the use of tables, graphs, and equations.
Mathematical Practice 6: Attend to precision.
Students must be precise when writing and using the equation to solve the problem, when specifying units of measure, when labeling the axes on their graph, and when communicating their reasoning during their presentation.
Mathematical Practice 7: Look for and make use of structure.
Students will use the structure of a problem-solving plan to help them solve a different problem. Through this problem, students will explore the structure of the problem-solving model so they can apply it to other situations throughout this unit.
Interventions
Student has difficulty getting started.
- Restate the problem to your partner in your own words.
- Substitute easier numbers in the problem and solve it. How can you use those same strategies to solve the same problem with more difficult numbers?
- What problem-solving strategies or tools can you use to help you solve the problem?
- What information do you know, and what are you trying to find?
Student has an incorrect solution.
- Is your answer reasonable?
- How can you use the table to decide if your answer is reasonable?
- Does the information in your graph match your solution?
Student has a solution but is having difficulty articulating his or her thinking.
- How can you describe your thinking to somebody who is struggling?
- How can you state your answer as a complete sentence?
- Does your answer make sense? How do you know?
Student has a correct solution.
- What are some common errors you must watch out for when solving these types of problems?
- Write a Challenge Problem using this information and trade problems with your partner.
- How can you use a different tool (e.g., table, graph, or equation) to solve this problem?
Answers
- The rule tells me how far away lightning is for a certain number of seconds between the lightning and the sound of the thunder.
- The rule says that the distance in miles is the time between the lightning and the sound of the thunder divided by 5.
- The quantities that vary are time and distance.
- Distance = time ÷ 5
- The independent variable is time and the dependent variable is distance.
Work Time
Understand the Situation
Do you remember the last time you watched the sky glow with streaks of lightning and listened to the resonating claps of thunder? You may have wondered how far away the lightning was from where you stood.
There is a simple rule that says: "The distance of lightning in miles is the time in seconds between the appearance of the lightning and the sound of the thunder, divided by 5." Watch the video again to count the seconds between the lightning and thunder.
To analyze this problem of how far away the lightning is, you need to start by understanding the situation. Think about these questions:
- What does the rule tell you about the type of problems you will be solving?
- What information does this rule provide?
- What are the quantities that vary (that is, what are the variables)?
- How are these variables related?
- Which variable is the dependent variable and which is the independent variable?
VIDEO: Lightning and Thunder
Hint:
A quantity is an amount that can be measured. What can you measure in this situation?
Represent the Situation Mathematically
Lesson Guide
Students create a table and write an equation to represent the relationship between the time it takes sound of the thunder to reach a person and the distance of the lightning. Then they graph the relationship.
SWD: Some students with disabilities may have difficulty connecting newly introduced information with previously learned concepts. Help students to make connections between what they have learned in previous lessons about ratios, graphs, and equations and how ratios, graphs, or equations might be used to represent what they know about using time to measure the distance of lightning.
ELL: When forming groups, be aware of your ELLs and ensure that they have a productive learning environment. Different types of partnerships include:
- Pairing them up with English speakers so they can learn language skills
- Pairing them up with students who are at the same level of language skills, so they can take a more active role and they can work things out together
- Pairing them up with students whose proficiency level is lower, so they play the role of the "supporter"
- Pairing them up based on their math proficiency
Answers
- Ratio table:
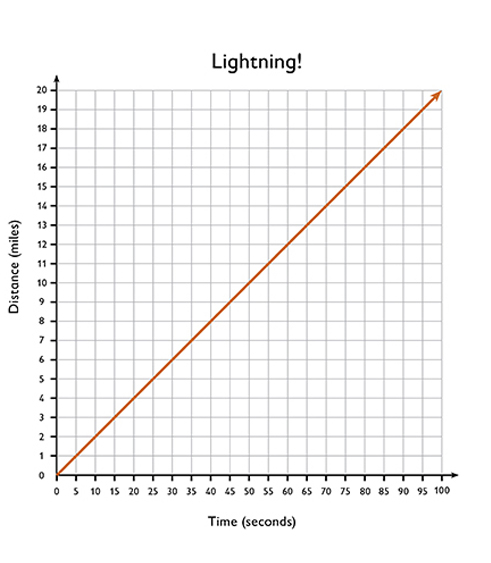
- Graph each column of the chart as a point (time, distance) on the graph.
- Formula:
- Let d = the distance in miles.
- Let t = the time in seconds.
d = t5
- Graph: x-axis = time (independent); y-axis = distance (dependent)
Work Time
Represent the Situation Mathematically
Now that you have used some easy numbers to represent the situation, it's important to make a general representation of the situation that will work for any numbers.
- Make a ratio table showing the relationship between time and distance.
- How could you use your completed ratio table to make a graph?
- Write a formula that shows the relationship between time and distance.
- Make a graph of this formula. How would you label the x-axis (independent variable) and the y-axis (dependent variable)?
- Make a graph of the formula for distances up to 20 miles.
Hint:
Use the pairs of numbers in your ratio table as points on your graph.
Answer Questions about the Situation
Lesson Guide
Now give pairs time to answer the question based on their representations of the problem situation.
Mathematics
As pairs work on answering the question using one of their representations, identify students to share in Ways of Thinking.
Look for students who:
- Use the ratio table to answer the question.
- Use the equation to answer the question.
- Use the graph to answer the question.
- Get an incorrect answer because they set up the representation of the problem situation incorrectly.
Answer
- The lightning is 2.4 miles away if there are 12 seconds between the lightning and the sound of the thunder.
Work Time
Answer Questions about the Situation
Use your formula and graph to answer this question about the situation.
- How far away is the lightning if there are 12 seconds between the lightning and the sound of the thunder?
Hint:
- Make sure you answer the question in the problem.
- Give your solution as a complete sentence.
Check That Your Answer Makes Sense
Lesson Guide
Now give pairs time to consider whether their answer makes sense given the problem situation.
Mathematics
Remind students of the importance of this step in the problem-solving process.
Answers
- Answers will vary. Possible answer: From the table I made, I can see that lightning travels 2 miles in 10 seconds and 3 miles in 15 seconds. Since I was trying to calculate the distance in 12 seconds, my answer should be somewhere between 2 and 3 miles, and it is. I know that it is closer to 2 miles since 12 seconds is closer to 10 seconds than it is to 15 seconds.
Work Time
Check That Your Answer Makes Sense
Think about the last time you observed lightning and thunder. Then look back at your answer to the question about how far away the lightning is when the time between the lightning and thunder is 12 seconds.
- Does your answer make sense based on your observations?
Hint:
Replay the video to see whether your answer also makes sense for the situation in the video.
A Different Question
Lesson Guide
Modify the amount of time given for the problem based on the class performance. Not all students may be able to finish, but when most of the class has completed the problem, have them work on their presentations.
As students work, identify students who used different strategies to solve the question.
Look for students who:
- Use the equation to answer the question.
- Use the graph to answer the question.
- Use the rate table to calculate a unit rate to answer the question.
- Use proportionality to answer the question.
When selecting students to present, look for students who:
- Use the equation as it was written (distance = time • 5) and then solve the one-step equation for the missing variable (time).
- Manipulate the equation to rewrite it as a function of time (time = distance ⋅ 5).
Answers
7 = t • 5
t = 5 • 7
t = 35
If lightning is 7 miles away, the time between the lightning and the sound of the thunder is 35 seconds.
Work Time
A Different Question
Here is a different question about the same situation.
- If lightning is 7 miles away, what is the time between the lightning and the sound of the thunder?
Hint:
- Can you use your ratio table to help you solve this problem?
- Is the ratio for this problem the same as the ratio in your table?
Prepare a Presentation
Preparing for Ways of Thinking
Remind students of the importance of the "check that your answer makes sense" step in the problem-solving process. Identify students to share in Ways of Thinking.
Look for students who:
- Get an incorrect answer and revise their answer because it does not make sense.
- Get a correct answer and understand why their answer makes sense.
ELL: When listening to students' responses, give students advance notice they will be presenting their work on a specific problem during the Ways of Thinking section. This will give them ample time to prepare a thoughtful response.
Challenge Problem
Answer
- The speed of sound is 1 mile per 5 seconds, or of a mile per second
Work Time
Prepare a Presentation
In this lesson, you went through a problem-solving process:
- Understand the Situation
- Represent the Situation
- Answer Questions about the Situation
- Check That Your Answer(s) Makes Sense
How did following that process help you solve any problems about how far away the lightning is in miles?
Support your explanation with examples from your work.
Challenge Problem
Light travels at a speed of approximately 180,000 miles per second. Thus, you see lightning almost instantaneously after it strikes.
However, sound travels more slowly, which is why you hear thunder only after you have already seen the lightning (generally—it’s possible that you might sometimes hear thunder without having seen any lightning). The differences in the speed of light and the speed of sound account for this occurrence. The greater the distance of the lightning, the greater the delay between the appearance of the lightning and the sound of the thunder.
- What is the speed of sound?
Make Connections
Lesson Guide
Have pairs give their presentations.
Highlight the strategies students used to solve the problems. Encourage classroom discourse regarding the approaches for solving the problems and the validity of the answers. Prompt students to give the presenters positive feedback as well as opportunities for improvement. Students should be refining their own processes, correcting solutions, and taking notes during Ways of Thinking.
Ask guiding questions:
- When creating the graph of this data, what variable did you select for the x-axis? What variable did you select for the y-axis? Why? How does this affect the shape of the data?
- Which tool do you prefer to use to solve this problem—the table, the graph, or the equation? Why? Did anyone find another strategy for solving this problem?
- Which strategy would provide a more accurate solution to the problem, using the equation to find the distance to the lightning or using the graph? Why do you think this approach provides more accurate results?
- How can you use the table to calculate a unit rate to help you solve this problem?
- What was the most challenging aspect of this problem? How did you overcome this obstacle?
- What connections can you make between this problem and other problems you have studied this year? What does it remind you of?
As a class, revisit the mathematical goals and outline the steps taken to generate a problem-solving plan. Create a poster to post in the classroom. Have the students create notes on the Problem-Solving Steps so they can have a record to reference as well.
Problem-Solving Steps
- Understand the situation:
- What is the problem asking you to find out?
- What information is given to solve the problem?
- What are the quantities that vary?
- How are the variables related?
- Which variable is independent? Dependent?
- Represent the situation:
- Tables
- Graphs
- Equations
- Answer questions about the situation.
- Check that your answer makes sense.
- Prepare a presentation:
- Write your answer as a complete sentence.
- Support your answer with words, pictures, numbers, diagrams, equations, and so on.
- Explain why your answer makes sense.
- Use your analysis to solve other problems.
SWD: As students present their solutions, make connections between different solutions to the same problem. This allows students to see the multiple ways to solve/analyze a problem. Write down all important connections, and have students copy into their Notebook.
Performance Task
Ways of Thinking: Make Connections
- Take notes about the strategies and tools that your classmates discuss in their presentations.
- As you listen to the presentations, think about the ways that each classmate used the steps of the problem-solving process. Which step(s) do you think were the most helpful for each individual in solving the problem?
Hint:
As your classmates present, ask questions such as:
- Can you explain how you made your graph?
- How did you decide which measurement units to use for time and distance?
- How did you know your answer was reasonable?
- What tool did you find to be the most helpful for solving the problem? Why?
- What did you do to understand the situation?
- Did you have any errors in your thinking? If so, what were they and how did you correct them?
- How does knowing the time relationship between lightning and thunder help you calculate the distance of lightning from you?
- What mathematical strategies are the most useful in solving a problem in which you are given a relationship between variables and are asked to make predictions?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Give students solo time to respond to the prompt. Review the reflections to learn what mathematical connections students see between lightning and thunder.
If time permits, select students to read their responses aloud. Encourage classmates to “add a thought” to the responses given.
SWD: Some students may struggle with the task of writing a reflection of the lesson. Possible supports:
- Prior to writing the reflection, have students discuss their ideas with a partner or adult and rehearse what they might write.
- Allow students to map out their ideas in outline form or in a concept web.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
When I think about lightning and thunder, I see these connections …