- Author:
- Chris Adcock
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
85 Milliliters
Drips
Leaky Faucet Timelapse
Time-Lapse Birthday Candles
Gallery Problems Exercise

Overview
Lesson Overview
Allow students who have a clear understanding of the content in the unit to work on Gallery problems of their choosing. You can use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery
Map Reading
Students will examine a street map, interpret the street map coordinates, and relate the street map to an x-y coordinate grid.
Burning Candles
Students will explore how the height of a burning candle changes with time. In one case, they will get information by watching a video of candles burning. In another case, they will be given data with which they can calculate a candle's height at any given time.
More Directions
Students are given instructions on what path to take to get to a friend's house. But these instructions are incomplete because a starting point is not given. Their task is to figure out which starting points will make these instructions work.
Leagues
Students will determine how the length of a sports league's playing season is affected by increasing the number of teams from 22 to 30. They will use the number of times a game can be played each week and the present length of the season to solve the problem.
Traffic
Students will figure out the distance between cars on a highway and how many cars there are along a 1-mile stretch of the highway. They will use the speed of the cars and how often a car passes a certain point to solve the problem.
Leaky Faucet
Students will watch a video of a sink filling with water. From that, they will determine how long it will take for the sink to fill up completely.
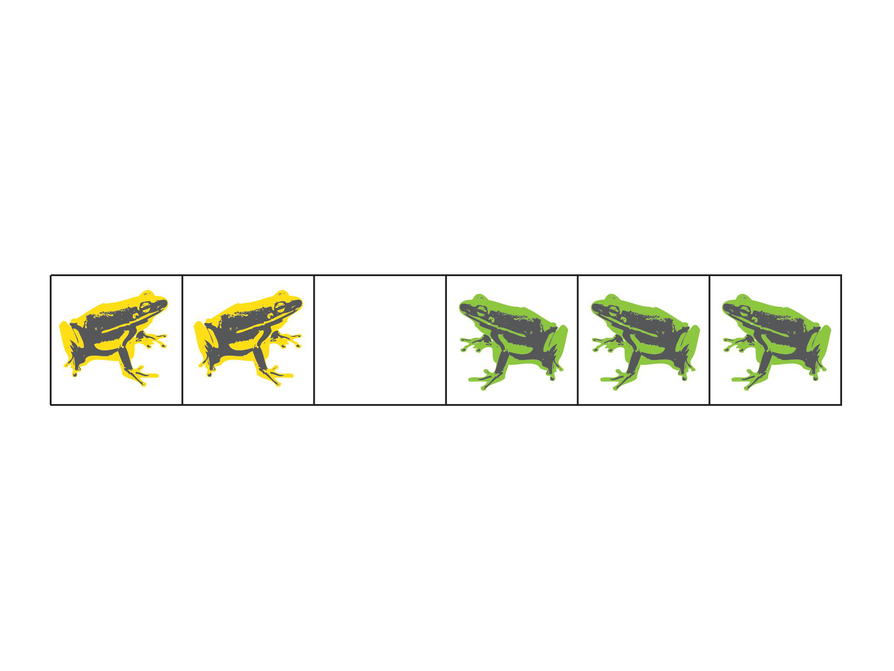
Frog Jump
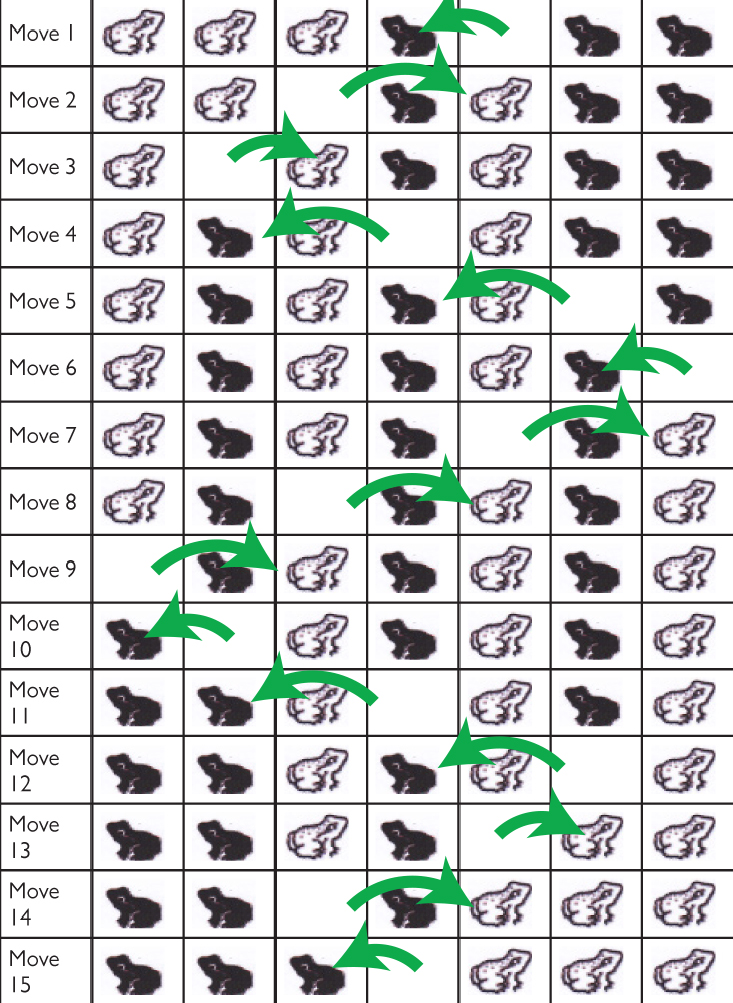
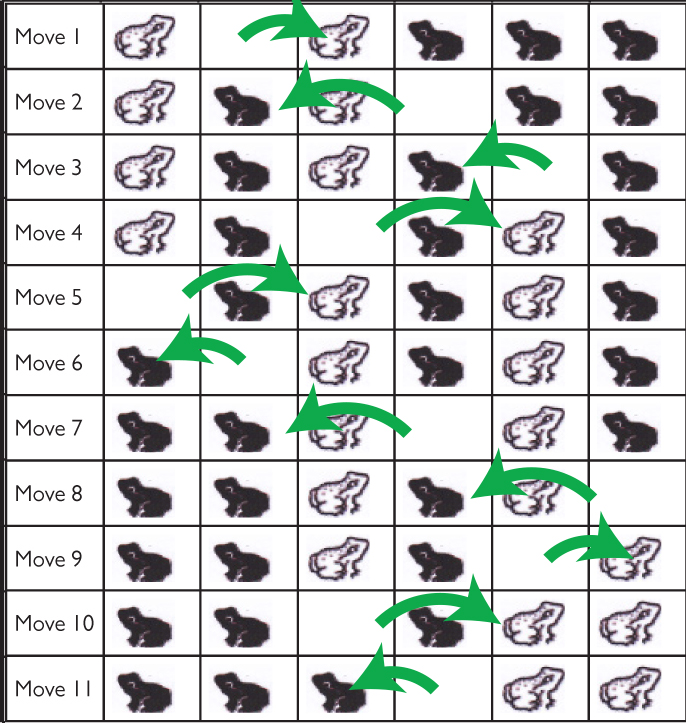
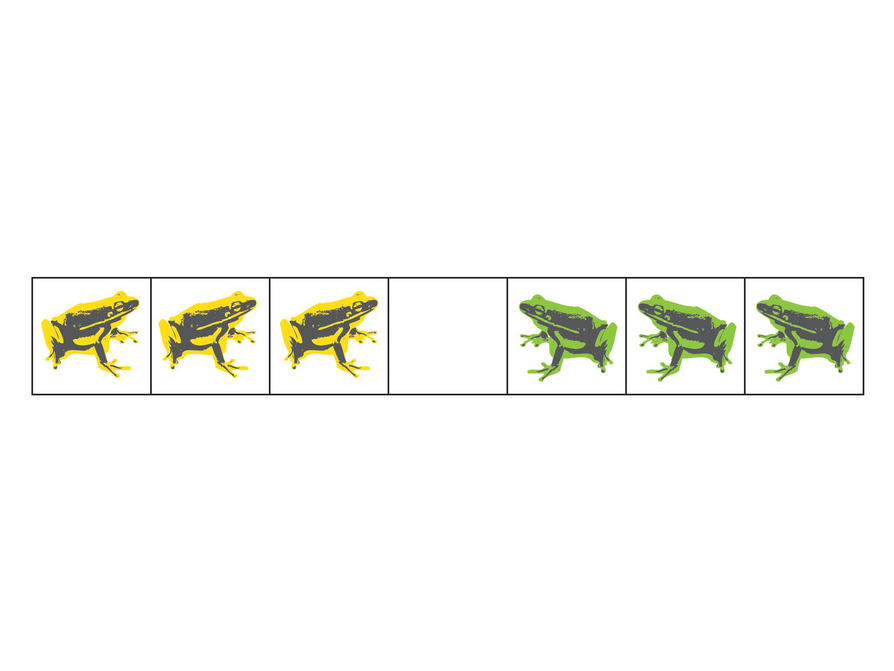
Students are shown a drawing of yellow and green frogs arranged in a straight line. The yellow frogs are on the left, and the green frogs are on the right. Their task is to figure out how the yellow and green frogs can switch positions if they can move only by leaping according to certain rules.
Map Reading
Answers
- The W means the street runs horizontally, or from west to east, and lies west of Route 189. The 200 means that the location is 2 blocks away from Route 189, and the N means that the street is north of Center Street.
- Answers:
- The point (3, –1) is on the corner of S 300 E Street and E 100 S Street. The point (–4, l) is on the corner of N 400 W Street and W 100 N Street.
- The least number of blocks you would have to walk between these locations is 9 blocks.
- Answers will vary.
- Answers will vary.
- Answers will vary.
Work Time
Map Reading
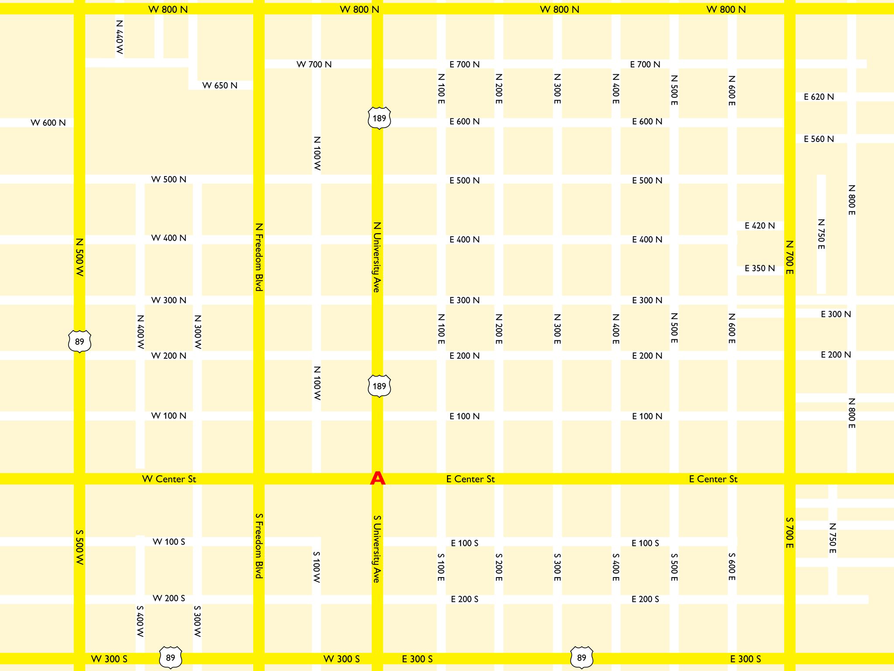
This is a street map of the city of Provo, Utah.
The street map can be thought of as a coordinate system. At the letter "A," you see the center of town, the origin of the street map coordinate system. The street map coordinates that are used here consist of names starting with W, E, N, or S, and number likes 100, 200, 300, etc., that are followed by W, E, N, and S.
- What does W 200 N Street mean? Find the street on the map.
- Imagine placing over the street map an x–y coordinate grid, whose origin is labeled A. The coordinates of the streets are given by the numbers 1, 2, 3, etc. Center Street can be seen as the x-axis, Route 189 as the y-axis.
- Where is the point with coordinates (3, –1)? And (–4, 1)?
- What is the smallest number of blocks you would need to walk to get from one of these points to the other?
- Create a problem for someone to solve by giving a route based on coordinate clues to find a specific location.
- How can you tell which streets are west of Route 189? What type of integer would you use on the x–y coordinate grid to represent these streets? What coordinate, x or y, represents east-west streets?
- How can you tell which streets are south of Route 89? What type of integer would you use to represent these streets? What coordinate, x or y, represents north-south streets?
Burning Candles
Answers
Part 1
- The candle in the video burns from the bottom up and then the top down. Candles in real life only burn in one direction, from the top down. This video could have been made by playing a video of a burning candle in reverse and then playing it forward.
This is a graph of the height of the blue candle over time. 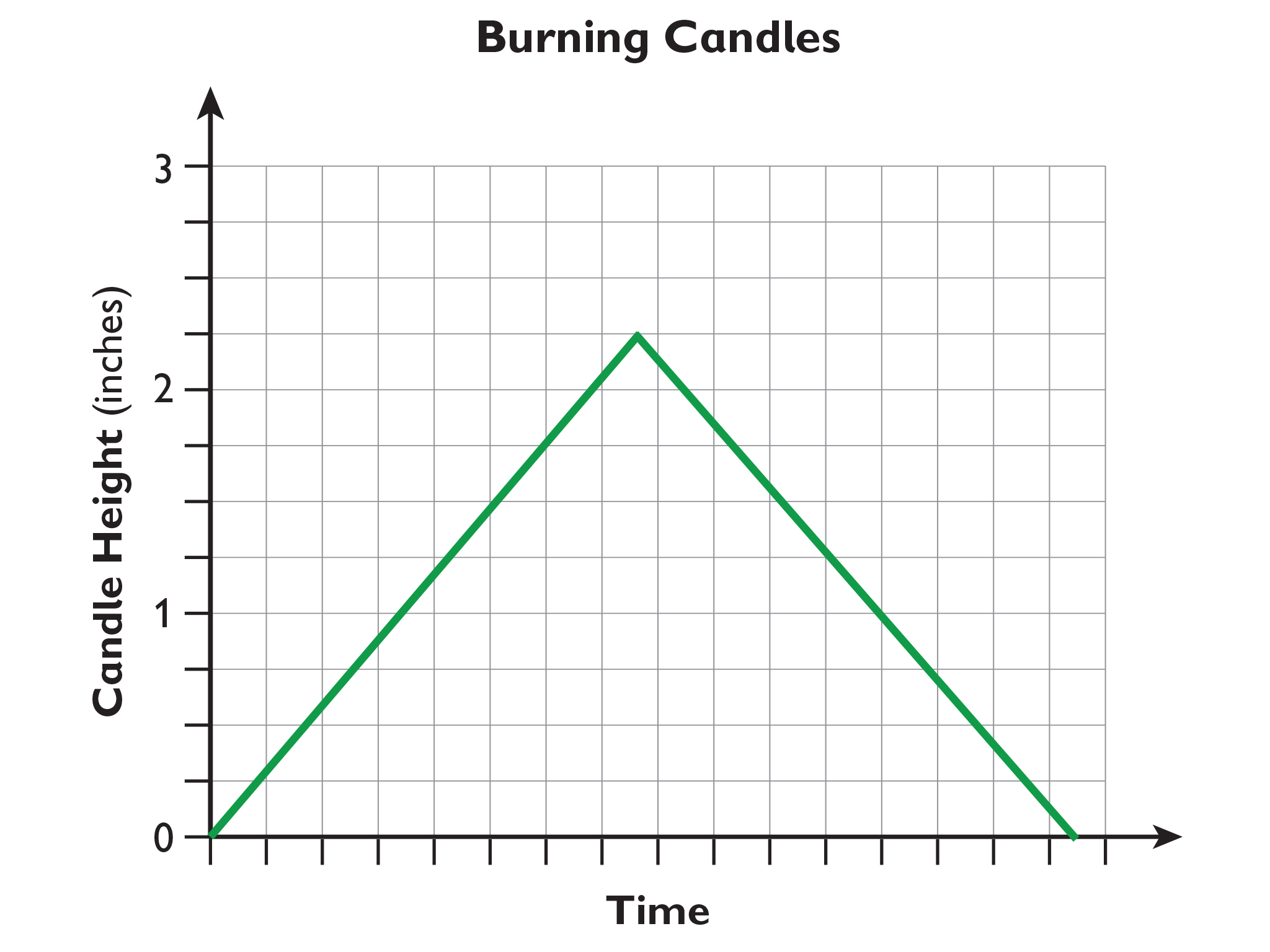
- This is a graph of the height of the candle on the right over time.
- After 30 hours, the candle would have burned 48 millimeters, so its height would be 72 millimeters.
- Most of the graphs of the burning candles would be a straight line descending towards the x-axis like the graph for Candle 1, because the candles are uniform throughout and would burn at a constant rate. The only graph that would look different would be the graph for Candle 5. Since this candle is tapered and not a uniform width throughout, the candle would not burn at a constant rate, it would burn faster at first and then more slowly. The line would still be descending but not straight.
Work Time
Burning Candles
Part 1
- Watch the video. Compare and contrast how the candle in the video burns compared to a candle in real life. How do you think this video was made?
- Create a graph that shows what happened to the height of the blue candle over time. (Height of the candle means height of the top of the candle.)
- Represent time on the horizontal axis and height on the vertical axis.
- To make your graph, first use the given information to calculate the candle height at different times. Then make a two-column table with time in one column and candle height in another column. Use your table to help create your graph.
Part 2
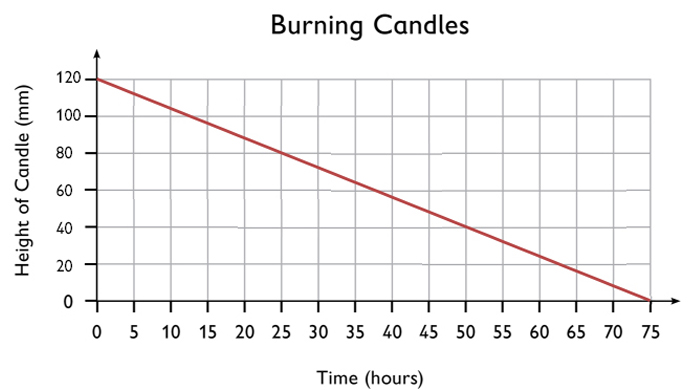
Before the candle on the right starts burning, it has a height of 120 mm. Its burning time is 75 hours and it burns at a constant rate
- Draw a graph that shows what happens to the height of the candle on the right over time.
- Use the graph to find the height of the candle after 30 hours of burning.
- If you graphed the height of each of the candles in the picture as the candle burned, do you think all of the graphs would be straight lines? Why or why not?
VIDEO: Time-Lapse Birthday Candles
More Directions
Answers
- Answers will vary. Possible answer: You can find Doug's house on the map and work backwards through his directions to find the ice cream shop.
- See artwork for number 3.
4. Possible answers (students should include both of these locations on their map):
- 10th Avenue and C Street
- 4 th Avenue and G Street
Work Time
More Directions
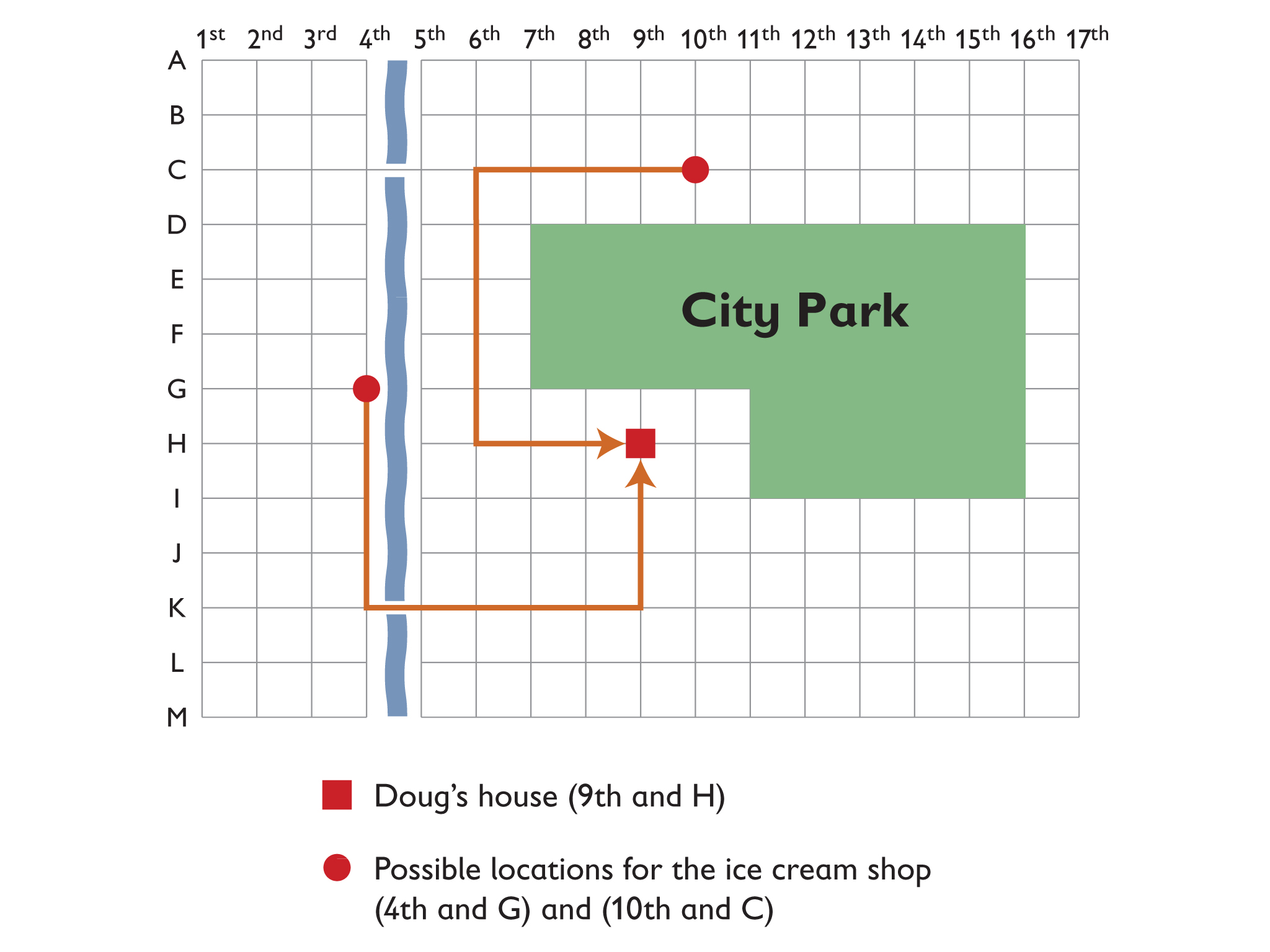
Your friend Doug gave you directions for how to bike to his house from his favorite ice cream shop in town. You are not sure which ice cream shop he meant.
Doug’s house is at the corner of H Street and 9th Avenue.
Here are the directions Doug gave you:
- Bike straight for 4 blocks and turn left.
- Bike straight for 5 blocks and turn left again.
- Bike straight for 3 blocks and you are at my house.
- How can you use a street map to help you figure out where his favorite ice cream shop is?
- Draw a street map showing the streets from 1st through 17th Avenue, and A through M Street.
- Add the following features to your map.
- A river runs between 4th and 5th Avenue.
- There are two bridges for getting across the river, one at C Street and one at K Street.
- City Park is "L"-shaped and has corners at 7th and G, 7th and D, 16th and D, 16th and I, 11th and I, and 11th and G. You are not allowed to bike across City Park.
- Where is Doug’s favorite ice cream shop located? Show all possible locations and the possible paths you will take to Doug’s house on the map.
Leagues
Answers
- 22 • 21 = 462
22 teams require 462 matches in all.
462 ÷ 35 = 13.2
This is an average of 13.2 matches per week, or about 13 games per week for 28 weeks and 14 games per week for 7 weeks.
- 30 • 29 = 870
30 teams require 870 matches in all.
29 • 2 = 58
Each team plays 58 matches.
870 ÷ 13.2 = 65.90If the league still plays an average of 13.2 matches per week, 870 matches would take about 66 weeks. But if one assumes that each team provides a home field, the season may still only last about 35 weeks.
Division
Work Time
Leagues
A top division has 22 teams. Each team plays all the other teams twice, once at home and once away. Games are usually played on Saturdays, but sometimes on Wednesdays, too. The season lasts about 35 weeks. There is a proposal to expand this top division to 30 teams.
- How many matches in all would be played and how many matches would each of the 22 teams play?
- What would the effect of expanding to 30 teams be on the length of the playing season?
- What operation can help you “share” the matches evenly between the weeks?
Traffic
Answers
Situation A:
- The distance from the front of one car to the front of the next car is 88 feet if the cars are traveling 88 feet per second and passing by each second.
- 5,280 feet ÷ 88 feet = 60. There are 60 cars per 1-mile stretch of highway.
Situation B:
You can use the same proportional reasoning as the first problem to calculate your answer, or you can use the relationship between the speeds.
- Since the car is traveling at half the speed as the original situation, the distance between the front of the cars would be half as much; therefore, there are 44 feet between the front of each car. When the cars travel slower, it would take more cars on the road to see them pass by every second; therefore, the number of cars on a 1-mile stretch of highway would double.
- There would be 120 cars on the 1-mile stretch of highway.
Situation C:
You can use the proportional reasoning presented in the first problem to calculate the answer and then compare the effect that the speed has on the number of cars and the distance between the front of each car, or you can use the relationship between the speeds.
- The cars in this problem are traveling 2.5 times faster than the cars in the second situation 75 ÷ 30 = 2.5, but that is not every second. It is every 2 seconds, so you would double this time to get a result of 5 seconds. Since the cars are going 5 times faster, they would be 5 times farther apart, so the front of each car would be 220 feet apart ( 44 × 5 = 220). Since the cars are traveling faster, there would be fewer cars in the 1-mile stretch. There would be the amount of cars, and of 120 is 24 cars.
- You could also use the relationship between situation A and C to find your answer. In situation C, the cars are traveling 1.25 times faster each second (75 ÷ 60 = 1.25), so for every 2 seconds, they are going 2.5 times faster (1.25 × 2 = 2.5). If the cars are going 2.5 times faster, the distance between the front of each car would be 2.5 times greater, so the front of each car would be 220 feet apart (88 × 2.5 = 220). Since the cars are traveling faster, there would be fewer cars in the 1-mile stretch. There would be the amount of cars, and of 60 is 24 cars.
Work Time
Traffic
Situation A:
Monique stands by the highway. She notices that one car goes by every second. She knows that these cars are going 60 miles per hour.
- How many feet apart are the cars?
- How many cars are there on 1 mile of highway?
Justify your answers mathematically.
Think about 60 miles per hour as a ratio of 60 miles to 1 hour. Use this ratio to write a proportion that you could use to calculate the distance the car travels each minute and second.
Remember, there are 5,280 feet per mile.
Situation B:
One car goes by every second, but the cars are going 30 miles per hour.
- How many feet apart are the cars?
- How many cars are there on 1 mile of highway?
Justify your answers mathematically.
When the cars are traveling more slowly, what would happen to the distance between each car? How can you use the relationship between the speeds and the answer to Question 1 to help you calculate the distance between each car?
If you are still seeing a car every second and the cars are traveling more slowly than before, would there be more or less cars along a given length of the highway? How can you use the relationship between the speeds and the answer to Question 1 to help you calculate the number of cars on the 1-mile stretch of highway?
Situation C:
One car goes by every 2 seconds and the cars are going 75 miles per hour.
- How many feet apart are the cars?
- How many cars are there on 1 mile of highway?
Justify your answers mathematically.
How does the increase in time from 1 second to 2 seconds affect the problem?
How does this increase in time affect the distance between each car?
How does the increase in time affect the number of cars on the road?
How can you use the relationship between the original speed and the increased speed to help you calculate your answer?
Leaky Faucet
Answers
- Answers will vary. Students should make a hypothesis based on the information in the video.
- Answers will vary. Students should make two unreasonable hypotheses based on the video, one that is too low and one that is too high.
- Answers will vary. Possible answers: time between each drop, size of each drop of water, volume/size of the sink, number of water drops it would take to fill the sink, whether or not the water is dropping at a constant rate.
3 gal = 3 × 3,785.41178 mL = 11,356.23534 mL
It will take approximately 22 hours and 16 minutes to fill the sink.
- Answers will vary. Sample answer:
- The video shows the sink filling up more quickly than my calculations showed it would. Both my calculations and the video showed 22 hours, but the video had only an additional 4 minutes, instead of 16.
- The faucet might not have dripped at a constant rate, or maybe the size of the drops varied.
Leaky Faucet
How long will it take for the sink to fill up?
- Watch the video Drips. Write down a estimate of how long it will take for the sink to fill up based on what you see.
- Watch the video 5 Drops. Write down an estimate for filling the sink that you know is too high and an estimate that you know is too low.
- What information do you need to know in order to find the amount of time it will take the sink to fill up at the given drip rate?
- The sink holds 3 gallons. Use the information in the video 85 Milliliters to find how long the sink will take to fill.
- Watch the video Leaky Faucet Timelapse.
- How does your answer compare to the time recorded in the video?
- What might cause the similarities or differences between your calculations and the actual time?
VIDEO: Drips
VIDEO: 5 Drops
VIDEO: 85 Milliliters
VIDEO: Leaky Faucet Timelaspe
Frog Jump
Answers
Work Time
Frog Jump
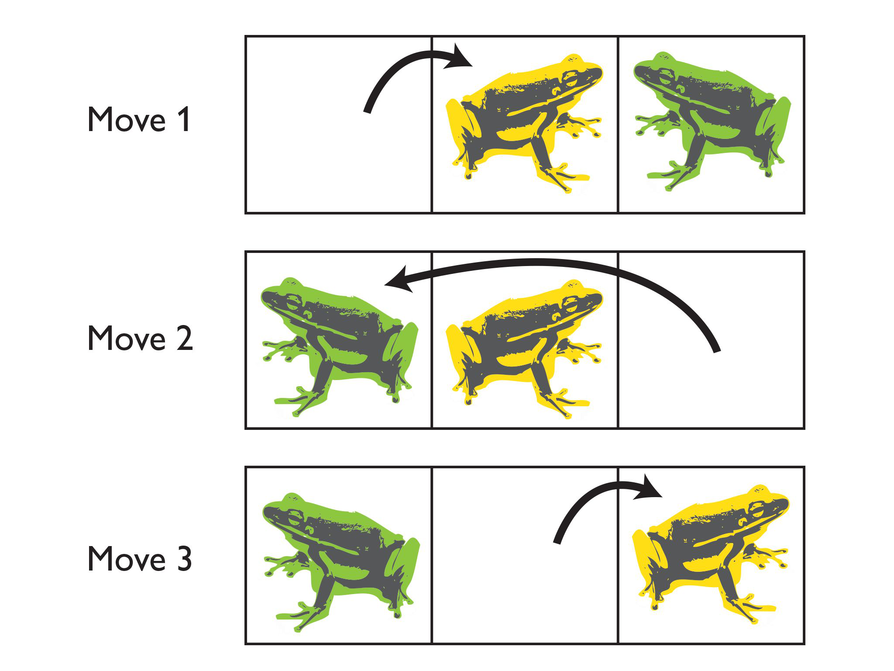
These two frogs can change places in three moves. The yellow frog starts in the leftmost box.
Rules:
- A frog can either hop onto an adjacent square, or jump over one other frog to the vacant square immediately beyond it.
- The yellow frogs can only move from left to right.
- The green frogs can only move from right to left.
- The frogs shown can be interchanged in 15 moves. Explain how.
- Now suppose that there are an unequal number of green and yellow frogs. These frogs can be interchanged in 11 moves. Explain how.