- Author:
- Chris Adcock
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
The Relationship Between Sound & Light

Overview
Students create and implement a problem-solving plan to solve another problem involving the relationship between the sound of thunder and the distance of the lightning.
Key Concepts
Throughout this unit, students are encouraged to apply the mathematical concepts they have learned over the course of this year to new settings. Help students develop and refine these problem-solving skills:
- Creating a problem-solving plan and implementing their plan systematically
- Persevering through challenging problems to find solutions
- Recalling prior knowledge and applying that knowledge to new situations
- Making connections between previous learning and real-world problems
- Communicating their approaches with precision and articulating why their strategies and solutions are reasonable
- Creating efficacy and confidence in solving challenging problems in a real world
Goals and Learning Objectives
- Create and implement a problem-solving plan.
- Organize and interpret data presented in a problem situation.
- Analyze the relationship between two variables.
- Create a rate table to organize data and make predictions.
- Apply the relationship between the variables to write a mathematical formula and use the formula to solve problems.
- Create a graph to display proportional relationships and use this graph to make predictions.
- Articulate strategies, thought processes, and approaches to solving a problem and defend why the solution is reasonable.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will analyze a simple rule for finding how many kilometers away lightning is.
Review the steps in creating a problem-solving plan. Point out the problem-solving poster in the classroom, or have students bring up the notes they took on Problem-Solving Steps:
Problem-Solving Steps
- Understand the situation:
- What is the problem asking you to find out?
- What information is given to solve the problem?
- What are the quantities that vary?
- How are the variables related?
- Which variable is independent? Dependent?
- Represent the situation:
- Tables
- Graphs
- Equations
- Answer questions about the situation.
- Check that your answer makes sense.
- Prepare a presentation:
- Write your answer as a complete sentence.
- Support your answer with words, pictures, numbers, diagrams, equations, and so on.
- Explain why your answer makes sense.
- Use your analysis to solve other problems.
Remind students that they will need to create and implement a plan for solving problems throughout this unit. If students get stuck on a problem, this problem-solving model is a good resource.
Encourage students to briefly share the strategies they used to solve the lightning problem in the previous lesson (e.g., rates, tables, graphs, equations, proportions).
Opening
Analyze the following problem: "How many kilometers away is the lightning?"
Think Kilometers
Lesson Guide
Have students rewatch the video of thunder and lightning.
After watching the video, have a student read the problem aloud. Make sure all students understand the instructions before beginning. After answering any clarifying questions, allow students 5 minutes of solo time to begin their work.
During the solo time, monitor students, taking note of those who are struggling with the problem. Refrain from offering assistance until students have had time to attempt the problem on their own.
After solo time, give students 15–20 minutes of partner time to complete the problem. Have students share their approaches and then agree on a problem-solving plan to solve the remainder of the problem. Encourage struggling students to review their Problem-Solving Steps notes to guide their thinking. Carefully monitor students for understanding by asking probing questions. Modify the amount of time given for the problem based on the class performance. Not all students may be able to finish, but when most of the class has completed the problem, move on to Ways of Thinking.
While students are working with their partners, carefully monitor students, looking for unique strategies, a variety of approaches, and any misconceptions. Identify students to present during Ways of Thinking and note your rationale for choosing those students.
If you see common misconceptions occurring in the class, address them during Ways of Thinking. Have a student present who originally began working the problem incorrectly but found his or her mistake and corrected it. Have the student explain his or her initial thinking about the problem and what tipped him or her off that the approach was incorrect. Highlight the common misconception to shed light on where students should watch for errors.
SWD: Help students with disabilities make connections between what they have learned in previous tasks about rates, tables, graphs, equations, and proportions.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of the given relationship between the sound of the thunder and the distance of the lightning to solve the problem.
Mathematical Practice 2: Reason abstractly and quantitatively.
Students will abstract the given situation involving the relationship between the sound of thunder and the distance of the lightning symbolically using equations, and quantitatively contextualize the situation through the use of units to attend to the meaning of the quantities.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students will construct a viable argument for the reasonableness of their solution as they prepare their presentation. They will have the opportunity to critique the reasoning of the presenters to help clarify confusion and correct misconceptions.
Mathematical Practice 4: Model with mathematics.
Students will model the situation through the use of tables, graphs, and equations.
Mathematical Practice 6: Attend to precision.
Students must be precise when writing and using the equation to solve the problem, when specifying units of measure, when labeling the axes on their graph, and when communicating their reasoning during their presentation.
Mathematical Practice 7: Look for and make use of structure.
Students will use the structure of a problem-solving plan to solve this problem. Through this problem, students will explore the structure of the problem-solving model so they can apply it to other situations throughout this unit.
Interventions
Student has difficulty getting started.
- Restate the problem to your partner in your own words.
- Substitute easier numbers in the problem and solve it. How can you use those same strategies to solve the same problem with more difficult numbers?
- What problem-solving strategies or tools can you use to help you solve the problem?
- What information do you know, and what are you trying to find?
- What tools are available to help you get started on the problem?
Student has an incorrect solution.
- How can you use your Problem-Solving Steps to ensure you have a complete response?
- Is your answer reasonable?
- How can you use the table to decide if your answer is reasonable?
- Does the information in your graph match your solution?
- How can you decide which variable is dependent and which is independent? Why is this important to know?
- How can you label the units in the problem to check for reasonableness?
Student has a solution but is having difficulty articulating her thinking.
- How can you describe your thinking to somebody who is struggling?
- Does your answer make sense? How do you know?
- How can you state the answer as a complete sentence?
Student has a correct solution.
- What are some common errors you must watch out for when solving these types of problems?
- Write a Challenge Problem using this information and trade problems with your partner.
- How can you use a different tool (e.g., table, graph, or equation) to solve this problem?
- How can you use your solution to the first lightning problem to calculate the distance of the lightning in kilometers without any additional information?
Possible Answers
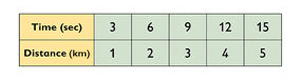
- Solutions will vary. Sample answer: Table:
- Equation:
- Let d = the distance in kilometers.
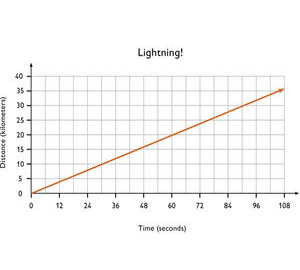
- Let t = the time in seconds. Graph: x-axis = time (independent); y-axis = distance (dependent)
- If there are 7 seconds between the sound of the thunder and the lightning, the lightning is 2.33… or kilometers away. From the table I made, I can see that lightning travels 2 kilometers in 6 seconds and 3 kilometers in 9 seconds. Therefore, my answer should be somewhere between 2 and 3 kilometers and it is. It is closer to 2 kilometers because 7 seconds is closer to 6 seconds than to 9 seconds.
Work Time
Think Kilometers
There is also a rule about lightning and thunder that works for kilometers rather than miles: The distance of lightning in kilometers is the time between the appearance of the lightning and the sound of the thunder in seconds, divided by 3.
Think about this rule and consider the following question:
- If there are 7 sec between the lightning and the sound of thunder, how far away is the lightning in kilometers?
- Follow the problem-solving process:
- Understand the situation.
- Represent the situation.
- Answer questions about the situation.
- Check that your answer makes sense.
VIDEO: Lightning and Thunder
Hint:
- Use the problem-solving process to help guide your thinking.
- What is the independent variable in the problem situation? What is the dependent variable? How can you represent these variables on your graph?
- How can you use a ratio table to help you make your graph?
- What intervals and scale will you use for your graph?
- Include the units for all quantities—in calculations, graphs, tables, and so on—to help you make sense of the values.
Prepare a Presentation
Preparing for Ways of Thinking
Highlight different solution strategies. Look for students who:
- Use unit rates from the table to answer the question.
- Use the graph to answer the question.
- Use the equation to answer the question.
- Use proportionality to answer the question.
- Have complete responses to the problem.
Watch for misconceptions; look for students who:
- Incorrectly identify the independent and dependent variables.
- Mislabel the axes on the graph (i.e., x as dependent and y as independent).
- Incorrectly write a rate for the problem (i.e., seconds per kilometer rather than kilometers per second).
- Use proportionality to solve the problem, but incorrectly set up their proportion.
- Have incomplete responses (e.g., missing representations, not fully describing the problem situation, incomplete presentation).
- Use the equation instead of .
- Use the commutative property with division to create the equation .
SWD: Partner Work provides students with the opportunity to work cooperatively by allowing students to negotiate, share ideas, and communicate with each other during problem solving. Such group-learning settings provide students with disabilities a chance to hear and use mathematical language while building their communication skills.
ELL: This is a good opportunity for students to share ideas with others by working cooperatively. This interaction helps students develop the second language.
Challenge Problem
Answers
- Answers will vary. Sample answer: The graphs are similar because the variables are on the same axes and both are linear relationships—as time increases, so does distance. The graphs are different because they use different units for the distance (miles versus kilometers) and different values for time and distance.
Work Time
Prepare a Presentation
Prepare a presentation about your findings.
Challenge Problem
- Compare your graph of the lightning and thunder formula in kilometers to your graph of the formula in miles. What is the same about the graphs? What is different?
Make Connections
Lesson Guide
Highlight the different strategies students used to solve the problem. Encourage classroom discourse regarding the approaches for solving the problems and the validity of the answers. Prompt students to give the presenters positive feedback as well as opportunities for improvement. Students should be refining their own processes, correcting solutions, and taking notes during Ways of Thinking.
Ask guiding questions:
- How can you decide which variable is dependent and which is independent? Why is this important to know?
- How can you use the problem-solving steps to ensure you have a complete response?
- When creating the graph of this data, what variable did you select for the x-axis? What variable did you select for the y-axis? Why? How does this affect the shape of the data?
- Is the equation the same as the equation ? Why or why not?
- Which tool do you prefer to use to solve this problem—the table, the graph, or the equation? Why?
- Which strategy would provide a more accurate solution to the problem, using the equation to find the distance to the lightning or using the graph? Why do you think this approach provides more accurate results?
- How can you use the table to calculate a unit rate to help you solve this problem?
- What was the most challenging aspect of this problem? How did you overcome this obstacle?
- What connections can you make between this problem and other problems you have studied this year? What does it remind you of?
Students should take note of any misconceptions they had when solving this problem. Have them highlight their individual errors and respond to those errors during the reflection.
ELL: As ELLs explain their reasons verbally and in writing, their answers may have language errors. Remember, language mistakes are natural. Focus on the content being communicated. Allow processing time. Do not emphasize grammar. Model standard English.
Performance Task
Ways of Thinking: Make Connections
Take notes about the process, strategies, and tools that your classmates used to solve the problem.
Hint:
As your classmates present, ask questions such as:
- How did you determine which variable is the dependent variable and which is the independent variable? Why do you need to know this?
- How can you use the problem-solving process to ensure that you have a complete response?
- Can you explain the connections between your diagram and your formula?
- How is this problem similar to finding the number of miles away the lightning is? How is it different?
- Why is it important to specify the unit for every quantity in your work?
- How does knowing the time relationship between lightning and thunder help you calculate the distance of lightning?
- Did you have any errors in your thinking? If so, what were they and how can you correct them?
- What mathematical strategies are the most useful in solving a problem in which you are given a relationship between variables and asked to make predictions?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out how solving a lightning problem in miles helped students to solve a lightning problem in kilometers.
During the reflection, have students discuss their individual misconceptions and errors and what strategies they may use to avoid these same errors in the future.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Solving a lightning problem in miles helped me solve a lightning problem in kilometers in these ways …