- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Regular Bears Equal Super Bears
The Relationship Between Size & Price 2.0

Overview
During this two-day lesson, students work with a partner to create and implement a problem-solving plan based on the mathematical concepts of rates, ratios, and proportionality. Students analyze the relationship between different-sized gummy bears to solve problems involving size and price.
Key Concepts
Throughout this unit, students are encouraged to apply the mathematical concepts they have learned over the course of this year to new settings. Helping students develop and refine these problem solving skills:
- Creating a problem solving plan and implementing their plan systematically
- Persevering through challenging problems to find solutions
- Recalling prior knowledge and applying that knowledge to new situations
- Making connections between previous learning and real-world problems
- Communicating their approaches with precision and articulating why their strategies and solutions are reasonable
- Creating efficacy and confidence in solving challenging problems in a real world
Goals and Learning Objectives
- Create and implement a problem-solving plan.
- Organize and interpret data presented in a problem situation.
- Analyze the relationship between two variables.
- Use ratios.
- Write and solve proportions.
- Create rate tables to organize data and make predictions
- Use multiple representations—including tables, graphs, and equations—to organize and communicate data.
- Articulate strategies, thought processes, and approaches to solving a problem and defend why the solution is reasonable.
Compare Results
Lesson Guide
Have students watch the videos. Give students time to discuss the following questions with their partners:
- Are these the same answers you got in the previous lesson?
- Why do these results vary from the answers to the previous lesson's problem?
- Do you think every Mini Bear is exactly the same? Why or why not?
After students have had time to talk with their partners, have a class discussion about why the answers they got through ratio, rates, and proportionality vary from when the gummy bears are actually weighed.
Students will be using the data from the videos to solve the problem in this lesson.
Opening
Compare Results
Watch the videos. Discuss these questions.
- Are the results in the videos the same as the results you found for the problem in the previous lesson?
- What could cause the number of Mini Bears and Regular Bears in each Super Bear to vary?
VIDEO: Mini Bears Equal Super Bears
VIDEO: Regular Bears Equal Super Bears
Math Mission
Lesson Guide
Discuss the Math Mission. Students will determine how to get the most gummy bear for the least amount of money.
Opening
Determine how to get the most gummy bear for the least amount of money.
Cost of Gummy Bears
Lesson Guide
This problem provides additional opportunities for students to try out their problem-solving strategies in a familiar context. Before beginning, review the Problem-Solving Steps 1–5 with students, and encourage them to open their Problem-Solving Steps notes to guide their thinking and reasoning while generating their plan.
Problem-Solving Steps
Understand the situation.
Represent the situation.
Answer questions about the situation.
Check that your answer makes sense.
Prepare a presentation.
Have students work on the problem solo for the first 3–5 minutes. During solo time, you should refrain from giving the students hints and pointers or from asking guiding questions. Give students an opportunity to develop their own unique problem-solving plan as well as time to organize the information presented in the videos. If over half of the class is struggling with the topic, give a hint such as, “Begin by understanding the problem and organizing the information from the videos.”
After solo time, allow students 10–15 minutes to work with a partner. Have students share their problem-solving plans. Carefully monitor students for understanding by asking probing questions. Modify the amount of time provided based on the class performance. When most of the class is done, move on to Ways of Thinking.
- What is the problem asking you to find out?
- What information is given to solve the problem?
- What are the quantities that vary?
- How are the variables related?
- Which variable is independent? Dependent?
- How can you create a table to represent the situation?
- How can you create a graph to represent the situation?
- How can you write an equation to represent the situation?
- Write your answer as a complete sentence.
- Support your answer with words, pictures, numbers, diagrams, equations, and so on.
- Explain why your answer makes sense.
SWD: Pair students who need some help with students who can peer tutor them on the problem-solving plan or on the various strategies (rate tables, graphs, proportions, etc.).
ELL: When listening to pairs interact, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a foreign language. Be sure to listen for meaning and not correctness of grammar. Encourage students to ask each other probing questions if the meaning is not apparent. This partner time will help students during reflection time.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students must make sense of the relationship between the number of gummy bears and the cost of the gummy bears from the information presented in the videos and the table to determine which type is the best buy.
Mathematical Practice 2: Reason abstractly and quantitatively.
Students will abstract the given situation involving the relationship between the number of gummy bears and their cost symbolically using equations, rates, ratios, and proportions to quantitatively contextualize the situation.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students will construct a viable argument for the reasonableness of their solution as they prepare their presentation. They will have the opportunity to critique the reasoning of the presenters to help clarify confusion and correct misconceptions.
Mathematical Practice 4: Model with mathematics.
Students will model the situation through the use of tables, graphs, and equations.
Mathematical Practice 5: Use appropriate tools strategically.
Students will select and use appropriate tools, including calculators, to help them find the cost for 2,250 grams of gummy bear or how many bears they can buy with $29.95.
Mathematical Practice 6: Attend to precision.
Students must be precise when writing and using an equation to solve the problem, when specifying units of measure, when labeling the axes on their graph, and when communicating their reasoning during their presentation.
Mathematical Practice 7: Look for and make use of structure.
Students will use the structure of a problem-solving plan to help them solve this problem. Through this problem, students will explore the structure of the problem-solving model so they can apply it to other situations throughout this unit.
Interventions
Student has difficulty getting started.
- How can you organize the information from the video with the data given in the table?
- How can you label the units on your ratio to help you correctly write your proportion?
- How can you find a unit cost to help calculate your answer?
- Restate the problem in your own words.
- What are the quantities in this problem and how do they vary?
- How can you find the number of Mini Bears and Regular Bears you can buy for $29.95? How can knowing this help you find your solution?
- How can you find how many packages of Mini Bears and Regular Bears you would need to buy to have the same amount of candy as the Super Bear? How can knowing this help you find your solution?
Student has an incorrect solution.
- Is your answer reasonable?
- How can you use a table or graph to check your answer?
- How can you label the units in your problem to check for reasonableness?
- How can you use your Problem-Solving Steps to ensure you have a complete solution?
Student has a solution but is having difficulty articulating her thinking.
- How can you describe your thinking to somebody who is struggling?
- How can you state your answer as a complete sentence?
- Is your answer reasonable? How do you know?
Student has a correct solution.
- Create a Challenge Problem with this data and trade problems with your partner.
- Use and explain a different strategy to solve this problem.
- What are some common errors and misconceptions you must watch out for when solving similar problems?
Possible Answers
Solutions will vary.
1,791 Mini Bears = 1 Super Bear
962 Regular Bears = 1 Super Bear
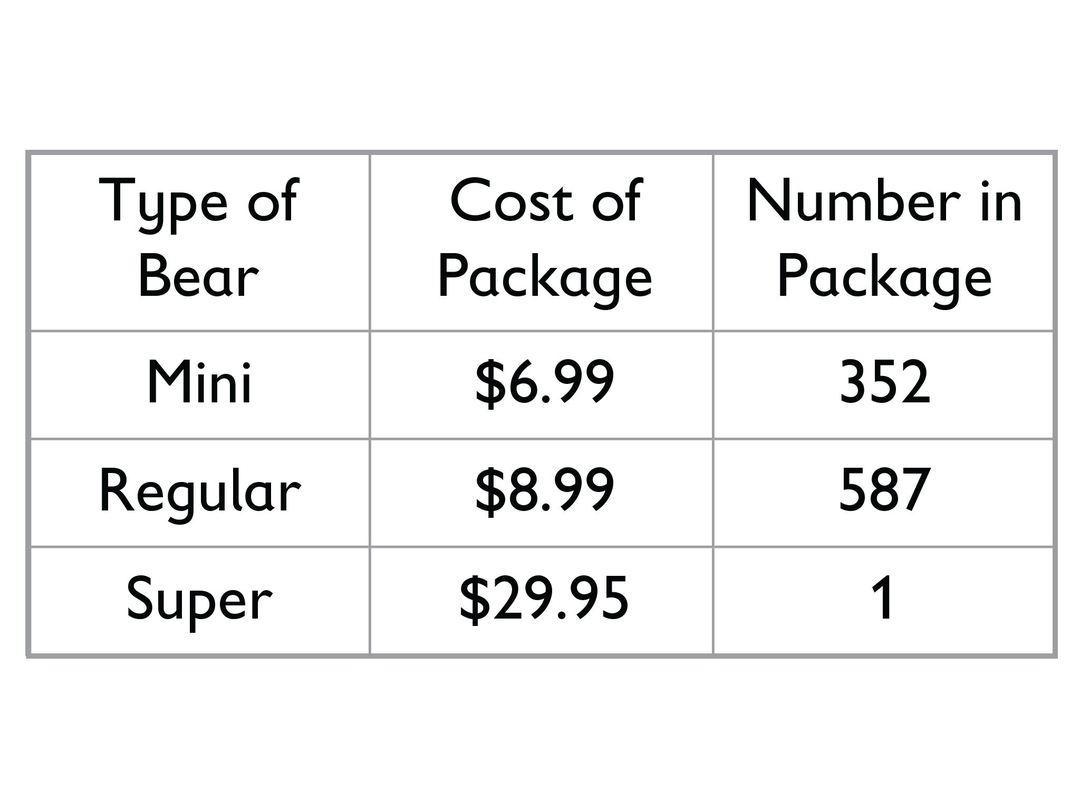
1 package of 352 Mini Bears costs $6.99.
1 package of 587 Regular Bears costs $8.99.
Each Super Bear costs $29.95.Buying the Regular Bears gives you the most gummy bear for your money.
Regular Bears are the best buy because it would cost $14.73 for the same weight in Regular Bears as a Super Bear that costs $29.95, saving you $15.22. (8.99 ÷ 587) · 962 = 14.73
Or, you could buy approximately 1,956 Regular Bears with $29.95; the video shows that it takes about 962 Regular Bears to equal the same weight as 1 Super Bear.
Or, you could buy 962 Regular Bears to equal 1 Super Bear.
962 ÷ 587 = 1.64You can't buy a partial package, so you will need two packages.
8.99 · 2 = 17.98
You can get more gummy bears than the Super Bear by buying 2 packages of Regular Bears for $17.98. Or, you can buy 3 packages of Regular Bears for $26.97, which is a lot more bear than the Super Bear.
Check: From looking at the table, you can see that it would take just under 2 packages of Regular Bears to equal the same weight as 1 Super Bear. Since each package of Regular Bears is $8.99, it would cost less than $18 for the same amount of candy in Regular Bears as 1 Super Bear, making it the best deal. I can see that it would take about 5 packages of Mini Bears to give the same weight as the Super Bear, and since each package costs $6.99, it would take about $35 for the same amount of candy.
Work Time
Cost of Gummy Bears
This table shows the cost of different types of gummy bears.
If you wanted to eat a lot of gummy candy, which package would you buy in order to get the most gummy bear for the least amount of money?
- Use the information in the table and the videos to think about this problem.
- Then use the problem-solving process to answer the question:
- Understand the situation.
- Represent the situation.
- Answer questions about the situation.
- Check that your answer makes sense.
Hint:
- Use ratios to help you organize the information from the videos. Make sure to include the appropriate units.
- How can you find the number of each type of gummy bear that you can buy for $29.95? How can this information help you solve the problem?
Prepare a Presentation
Preparing for Ways of Thinking
As students work, identify students who used different strategies to share during Ways of Thinking. Look for students who:
- Write and solve proportions to answer the question.
- Use a unit cost to answer the question.
- Calculate the answer by finding how many bears of each type it would take to have the same amount (grams) as the Super Bear and then use these results to calculate the cost of that amount of bears.
- Calculate the answer by finding how many bears of each type they could buy with $29.95 and then compare these numbers to the data in the video.
- Use rate tables to answer the question.
- Solve the problem graphically with three lines on the same set of axes.
- Students who do or do not realize that you can't buy partial packages, and adjust their solutions accordingly.
Work Time
Prepare a Presentation
Prepare a presentation about how you solved the problem. Include any calculations, formulas, graphs, and/or diagrams that you used.
Make Connections
Lesson Guide
Highlight the different solution strategies students used to solve the problem. Focus on how students created and implemented a problem-solving plan. Encourage classroom discourse regarding the approaches for solving problems and the validity of the answers. Prompt students to give the presenters positive feedback as well as opportunities for improvement. Students should be refining their own strategies, correcting solutions, and taking notes during the presentations.
Ask guiding questions:
- How did you begin solving this problem? What was the first step?
- How did you create a problem-solving plan?
- What connections can you make between this problem and the gummy bear problem from the previous lesson?
- How can you use a unit rate to help you find the cost per gummy bear? How can you use a unit rate to find the number of bears (or weight in grams) you can buy for $1?
- How can you calculate the number of each type of bear you can buy with $29.95?
- How can you calculate the cost for 2,250 grams of each type of bear?
- How did you organize the information from the videos? How did you organize the information from the table?
- How can you use estimation to check the reasonableness of your answer?
- What was the most challenging aspect of this problem? How did you overcome this challenge?
- Which tool did you prefer to solve this problem? Why?
- How do you know your answer is reasonable?
SWD: Provide a safe setting for students with disabilities to ask questions about any misconceptions they may have. Help students break problems down by thinking aloud and asking questions that get them to think about the mathematics behind the problem and common misconceptions. It is also important to model the way in which the language translates to mathematical terms and to a sequence of operations.
ELL: Provide ELLs with sentence frames to support them in presenting their solutions and critiquing. Examples would be “I calculated the cost by … because … .” or “My reasoning behind my solution is … .” Examples for critiques would be “I don't quite understand how you came to the conclusion that … since … .” or “Please explain to me how you came to that conclusion since I can't see it myself.”
Performance Task
Ways of Thinking: Make Connections
As your classmates present:
- Take notes about the different approaches and representations your classmates used to solve the problem.
- Think about the problem-solving process. How did the process help you to answer this question?
Hint:
As your classmates present, ask questions such as:
- How did you use ratios to organize the information provided in the videos and the table?
- How did finding the number of each type of gummy bear you could buy for $29.95 help you solve the problem?
- How can you calculate the cost of 2,250 grams of each type of bear? How can this information help you solve the problem?
- How can you use unit rates to help you solve this problem? Which rate is most useful—cost per bear or bears per dollar? Why?
- How can you use the steps from the problem-solving process to ensure that your solution is complete?
- Can you write a formula to represent this situation?
- What are the variables in the problem? How are they related?
- How did you decide what units to use? Why is it important to include the units?
- Did you have any errors in your thinking? If so, what were they and how can you correct them?
- Can you show this relationship graphically? If so, how could you use your graph to find the solution to the problem?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to learn what strategies students used to solve the problem.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
The strategy I used to solve this problem is …