
Students will be able to see the relationship between theoretical probability and experimental probability by computing both at the same time.
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Provider:
- BetterLesson
- Date Added:
- 12/01/2022

Students will be able to see the relationship between theoretical probability and experimental probability by computing both at the same time.

Practice problems with experimental probability.
Khan Academy learning modules include a Community space where users can ask questions and seek help from community members. Educators should consult with their Technology administrators to determine the use of Khan Academy learning modules in their classroom. Please review materials from external sites before sharing with students.

Discusses the difference between theoretical and experimental probability and how to use what information you have in order to estimate the likelihood of a given outcome. [6:55]
Khan Academy learning modules include a Community space where users can ask questions and seek help from community members. Educators should consult with their Technology administrators to determine the use of Khan Academy learning modules in their classroom. Please review materials from external sites before sharing with students.
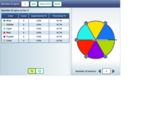
An interactive game for learning theoretical vs experimental probability.

In this activity, students can use the Probability Simulation application to roll a fair die and explore the Law of Large Numbers. They will conduct probability experiments that involve tossing a fair die, graph the results, compare the experimental probability to its theoretical probability and see how the Law of Large Numbers affects the results.

Samples and ProbabilityType of Unit: ConceptualPrior KnowledgeStudents should be able to:Understand the concept of a ratio.Write ratios as percents.Describe data using measures of center.Display and interpret data in dot plots, histograms, and box plots.Lesson FlowStudents begin to think about probability by considering the relative likelihood of familiar events on the continuum between impossible and certain. Students begin to formalize this understanding of probability. They are introduced to the concept of probability as a measure of likelihood, and how to calculate probability of equally likely events using a ratio. The terms (impossible, certain, etc.) are given numerical values. Next, students compare expected results to actual results by calculating the probability of an event and conducting an experiment. Students explore the probability of outcomes that are not equally likely. They collect data to estimate the experimental probabilities. They use ratio and proportion to predict results for a large number of trials. Students learn about compound events. They use tree diagrams, tables, and systematic lists as tools to find the sample space. They determine the theoretical probability of first independent, and then dependent events. In Lesson 10 students identify a question to investigate for a unit project and submit a proposal. They then complete a Self Check. In Lesson 11, students review the results of the Self Check, solve a related problem, and take a Quiz.Students are introduced to the concept of sampling as a method of determining characteristics of a population. They consider how a sample can be random or biased, and think about methods for randomly sampling a population to ensure that it is representative. In Lesson 13, students collect and analyze data for their unit project. Students begin to apply their knowledge of statistics learned in sixth grade. They determine the typical class score from a sample of the population, and reason about the representativeness of the sample. Then, students begin to develop intuition about appropriate sample size by conducting an experiment. They compare different sample sizes, and decide whether increasing the sample size improves the results. In Lesson 16 and Lesson 17, students compare two data sets using any tools they wish. Students will be reminded of Mean Average Deviation (MAD), which will be a useful tool in this situation. Students complete another Self Check, review the results of their Self Check, and solve additional problems. The unit ends with three days for students to work on Gallery problems, possibly using one of the days to complete their project or get help on their project if needed, two days for students to present their unit projects to the class, and one day for the End of Unit Assessment.

Students collect and analyze data for their unit project.Students are given class time to work on their project. Some students may choose to use the time to collect data (if their project is an experiment based on experimental probability), while others will use the tools (spinners, coin toss, number cube, etc.) to collect their data. Students should use the time to analyze their data, finding the theoretical (if possible) probability and comparing it to the experimental results.Key ConceptsStudents will apply what they have learned about probability to work on their project, including likelihood of events, determining theoretical and experimental probability, comparing results to calculations, and using simulations to establish probability.Students may also use data analysis tools to discuss their results.Goals and Learning ObjectivesComplete the project, or progress far enough to complete it outside of class.Review concepts of probability (simple probability, compound events, experimental vs. theoretical probability, simulations).
Lesson OverviewStudents will extend their understanding of probability by continuing to conduct experiments, this time with four-colored spinners. They will compare experimental results to expected results by first conducting an experiment, then calculating the probability of an event.Key ConceptsThis lesson takes an informal look at the Law of Large Numbers, comparing experimental results to expected results.Goals and Learning ObjectivesLearn about experimental probability.Compare theoretical probability to experimental probability and show that experimental probability approaches theoretical probability with more trials.Use proportions to predict results for a number of trials.

Students will extend their understanding of probability by continuing to conduct experiments with outcomes that do not have a theoretical probability. They will make predictions on the number of outcomes from a series of trials, and compare their predictions with the experimental probability calculated from an experiment.Key ConceptsStudents continue to investigate the Law of Large Numbers.Goals and Learning ObjectivesDeepen understanding of experimental probability.Use proportions to predict results for a number of trials and to calculate experimental probability.Understand that some events do not have theoretical probability.Understand that there are often many factors involved in determining probability (e.g., human error, randomness).
Students are able to to visualize the difference between theoretical and experimental probabilities with this computer based tool.

Students have their first encounter with probability, as they develop their understanding of probability through calculating theoretical probabilities and designing and running their own simulations.

This site is a virtual discussion between a teacher and student about probability and outcome. The virtual teacher poses wonderful questions for the students to think about. The virtual students then respond to the inquiries.

This lesson will introduce experimental and subjective definitions of probability. It is 1 of 3 in the series titled "Relative Frequency Probability/Empirical Method." Includes short quiz. [5:31]

This lesson will introduce experimental and subjective definitions of probability. It is 2 of 3 in the series titled "Relative Frequency Probability/Empirical Method." Includes short quiz. [7:12]

This lesson will introduce experimental and subjective definitions of probability. It is 3 of 3 in the series titled "Relative Frequency Probability/Empirical Method." Includes transcript of video and a short quiz. [5:26]

This interactive dictionary gives the definition of experimental probability. Be sure to follow the link to a discussion on probabilities and outcomes.

Looks at a marble experiment to see how the anticipated probability compares to the actual outcome. [7:02]
Khan Academy learning modules include a Community space where users can ask questions and seek help from community members. Educators should consult with their Technology administrators to determine the use of Khan Academy learning modules in their classroom. Please review materials from external sites before sharing with students.

Use our interactivity to simulate picking up a bow and some arrows and trying to hit the target a few times. Can you work out the best settings for the sight? This activity gives an opportunity to gather and collate data, and to test hypotheses, and is designed to be accessible to younger secondary maths students (grades 5, 6, 7, and 8).

If two goals are scored in a hockey match between two equally-matched teams, what are the possible scores? This activity gives an opportunity to investigate probability in the context of sport, and is designed to be accessible to secondary maths students at Key Stage 3.