- Author:
- Chris Adcock
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Coordinate Plane Plotter
Coordinate Point Plotter
Locate the Vertices
New Reflections
Reflections

Overview
Students reflect a figure across one of the axes on the coordinate plane and name the vertices of the reflection. As they are working, students look for and make use of structure to identify a convention for naming the coordinates of the reflected figure.
Key Concepts
- When point (m,n) is reflected across the y-axis, the reflected point is (−m,n).
- When point (m,n) is reflected across the x-axis, the reflected point is (m,−n).
- When point (m,n) is reflected across the origin (0,0), the reflected point is (−m,−n).
Goals and Learning Objectives
- Reflect a figure across one of the axes on the coordinate plane.
- Name the vertices of the reflected figure.
- Discern a pattern in the coordinates of the reflected figure.
Reflecting
Lesson Guide
Put a line on the floor with masking tape. Have a student stand on one side of the line in an interesting position, such as standing on one foot. Have another student stand on the other side of the line in a mirror image.
Now have students look at the images of the cars and the triangles. Discuss how each image has been reflected across the line to get a mirror image. Be sure students understand that each mirror image is the same size as the original and each original point and its mirror image are the same distance from the line of reflection.
Mathematical Practices
Mathematical Practice 7: Look for and make use of structure.
Review the importance of looking for and making use of structure in math. Remind students that they used the structure of a number line to decide if an inequality was true or false. Encourage students to look for structure in the math today. Tell students to find a pattern in the way the math works.
Opening
Reflecting
Read and Discuss
- You can reflect a figure across a line to get a mirror image of the figure.
- Every point is the same distance from the line of reflection, and the reflection, or mirror image, is the same size as the original image.
Reflect Points
Lesson Guide
Tell students that they will use the x- and y-axes on the coordinate plane to reflect points across the x- and y-axes.
Have pairs work through the problem and then discuss it as a class.
Opening
Reflect Points
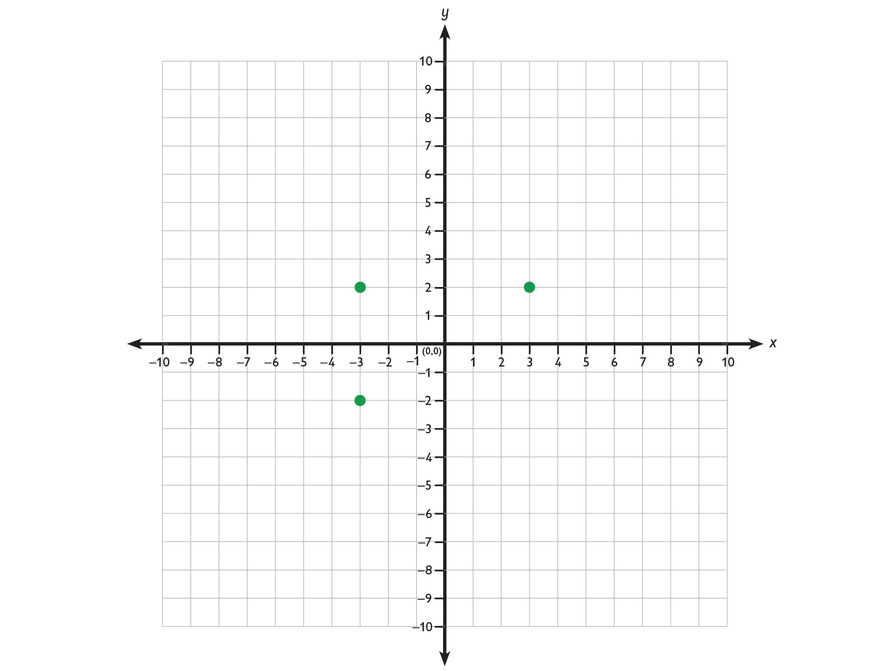
You can reflect a point across the x-axis or y-axis on the coordinate plane. In this case, the point (−3,2) has been reflected across each axis.
- What are the coordinates of the reflection of (−3,2) across the x-axis? The y-axis?
Reflect Figures
Lesson Guide
Have students reflect the figure and locate the vertices of the reflection.
Opening
Reflect Figures
Look for a pattern, or structure, as you reflect the figure in the Coordinate Point Plotter interactive.
- Locate the vertices of the mirror image, or reflection, of the figure.
- Use the x- or y-axis as the mirror.
- Reflect the figure across the x- or y-axis.
INTERACTIVE: Coordinate Point Plotter
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find a pattern for naming the vertices of a figure reflected across one of the axes on the coordinate plane.
Opening
Find a pattern for naming the vertices of a figure reflected across one of the axes on the coordinate plane.
Locate the Vertices
Lesson Guide
Tell students that they will continue solving reflection problems. Monitor and check students' work as they progress through the problems.
After students have worked individually on a few problems, have them share their strategy with a partner.
SWD: During Partner Work, monitor student discussions and provide guiding questions that help students see the mathematics and find their own way to a solution. If a student is struggling with a particular concept, hold an individual conference. If many students are struggling with a concept, pull a small group to discuss the concept.
ELL: Be sure that ELLs are productive during this activity and that they are paired in a way that will foster participation. Sometimes, pair them up with native English speakers so that ELLs can learn from their counterparts’ English language skills. At other times, pair them up with students at the same level of language skills, so ELLs can take a more active role and partners can work things out together.
Interventions
Student has difficulty getting started.
- What are you trying to do?
- What are the coordinates of the vertices of the original figure?
- What axis are you reflecting the figure across?
- What will you do first? Second?
Student has an incorrect solution.
- Explain how you reflected the figure across the axis.
- What does it mean to reflect a point across an axis?
- How do you know that the point is reflected across the axis correctly?
Student has a correct solution.
- What method did you use to reflect the figure across the axis?
- Did you reach any conclusions about the coordinates of the reflected figure’s vertices?
ELLs: In posing these questions, make sure that if the student involved is an ELL, your pace is adequate and you are providing ample wait time to allow for a thoughtful response.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Some students may get frustrated if their reflections and the originals do not match up. Look for students who persevere when trying to plot the reflections.
Mathematical Practice 6: Attend to precision.
Identify students who carefully plot the coordinates of the reflected figures. Compare their methods with students who just “eyeball” the reflections.
Mathematical Practice 7: Look for and make use of structure.
Watch for students who begin to see a pattern in the coordinates of the reflected vertices and plot the reflections using the pattern.
Work Time
Locate the Vertices
- Locate the vertices of each figure reflected across the x- or y-axis.
Use the Coordinate Plane Plotter interactive if you find it to be helpful.
HANDOUT: Locate the Vertices
INTERACTIVE: Coordinate Plane Plotter
Start with one vertex and find its reflection.
Prepare a Presentation
Preparing for Ways of Thinking
Have partners prepare a presentation together.
Observe how students are locating the reflections and identify different strategies that can be shared in Ways of Thinking.
Challenge Problem
Answers
- Answer will vary.
Work Time
Prepare a Presentation
Describe the process you used to find each reflected vertex.
Challenge Problem
- Choose a line of reflection that is not the x- or y-axis.
- Reflect the figure across the line on the coordinate plane.
Use the Coordinate Plane Plotter if you find it to be helpful.
HANDOUT: New Reflections
INTERACTIVE: Coordinate Plane Plotter
Make Connections
Lesson Guide
Have student pairs give their presentations.
Discuss the Work Time activity and students’ presentations. Ask questions such as the following:
- Compare [Name]’s and [Name]’s strategies.
- How are they the same?
- How are they different?
- Did anyone have trouble reflecting the figures to start? Tell us the different methods you tried.
- What do you notice about the ordered pairs that name the corresponding vertices of a reflected figure? (Answer: They only differ by their signs.)
Have students who did the Challenge Problem share their work.
Performance Task
Ways of Thinking: Make Connections
Take notes about the strategies you can use to reflect figures on a coordinate plane.
As students present, ask questions such as:
- What strategy did you use to reflect the figure?
- How is your strategy different from the other methods mentioned so far? How is it similar?
- How do you know that each point is reflected correctly?
- What did you notice about the coordinates of the reflected figure’s vertices?
Describe Reflections
A Possible Summary
If you have two ordered pairs and the first numbers in the pair are opposite, the points will be located on opposite sides of the y-axis. If you have two ordered pairs and the second numbers in the pair are opposite, the points will be located on opposite sides of the x-axis.
Additional Discussion Points
- When two ordered pairs differ only by their signs, the locations of the points are related by reflections across onme or both axes.
- When point (m,n) is reflected across the y-axis, the reflected point is (−m,n).
- When point (m,n) is reflected across the x-axis, the reflected point is (m,−n).
- When the point (m,n) is reflected across the origin (0,0), the reflected point is (−m,−n).
ELL: Make sure all students have this information in their notebook. Provide some students with certain things to listen for during this portion of instruction. Some students may need copies of the notes from this portion of the lesson.
Formative Assessment
Summary of the Math: Describe Reflections
Write a summary describing how to reflect images on a coordinate plane.
Check your summary.
- Do you include what you observed about the coordinates of the reflected points?
Check Your Understanding
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
Interventions
Student has difficulty getting started.
- What do you need to do?
- Approximately where will this figure be located on the coordinate plane?
- Can you find one point that meets one of the criteria?
- Can you find another point that meets a different criterion?
Student does not seem to understand what a coordinate (ordered pair) is.
- Where can you go to review the meaning of coordinates (ordered pairs)?
- What does the first number in the ordered pair tell you?
- What does the second number in the ordered pair tell you?
Student does not seem to understand the opposite of a number or has drawn a figure that does not meet the criteria for the opposite of a number.
- Where can you go to review information about the opposite of a number?
- What is an example of a number and its opposite? How would you write those numbers as an ordered pair? Where would that point be located on the coordinate plane?
Student does not seem to understand integers and non-integers or has drawn a figure that does not meet the criteria for non-integers.
- Where can you go to review integers?
- What is an example of two numbers that are both non-integers? How would you write those numbers as an ordered pair? Where would that point be located on the coordinate plane?
Student does not seem to understand absolute value or has drawn a figure that does not meet the criteria for absolute value.
- Where can you go to review absolute value?
- What is an example of two numbers that have equal absolute values?
Student produces a correct solution but does not give an explanation of why it is correct.
- How does your figure or design meet each of the criteria?
Student presents the work poorly.
- Is your work shown clearly?
- Have you given enough explanation and is it clear?
Student presents a correct solution.
- Can you find a different way to solve the problem?
Possible Answers
- Sample answer:
- Explanations will vary.
Formative Assessment
Check Your Understanding
Work on this Self Check by yourself.
- Create a figure or design on the coordinate plane that satisfies the following criteria:
- At least one vertex has coordinates that include a number and its opposite.
- At least one vertex has coordinates that are both non-integers.
- At least one vertex is in each quadrant.
- At least two vertices have x-coordinates that have equal absolute values.
- At least two vertices have y-coordinates that have equal absolute values.
- Label each vertex with its ordered pair, and explain how your figure or design meets the criteria.
Use the Coordinate Plane Plotter interactive if you find it to be helpful, but record your work on the handout.
HANDOUT: Check Your Understanding
INTERACTIVE: Coordinate Plane Plotter
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what strategies students found useful when reflecting a figure on the coordinate plane.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter if you find it to be helpful.
A strategy that I found useful in reflecting a figure on the coordinate plane is …