Evaluating Expressions

Overview
Students analyze how two different calculators get different values for the same numerical expression. In the process, students recognize the need for following the same conventions when evaluating expressions.
Key Concepts
- Mathematical expressions express calculations with numbers (numerical expressions) or sometimes with letters representing numbers (algebraic expressions).
- When evaluating expressions that have more than one operation, there are conventions—called the order of operations—that must be followed:
- Complete all operations inside parentheses first.
- Evaluate exponents.
- Then complete all multiplication and division, working from left to right.
- Then complete all addition and subtraction, working from left to right.
- These conventions allow expressions with more than one operation to be evaluated in the same way by everyone. Because of these conventions, it is important to use parentheses when writing expressions to indicate which operation to do first. If there are nested parentheses, the operations in the innermost parentheses are evaluated first. Understanding the use of parentheses is especially important when interpreting the associative and the distributive properties.
Goals and Learning Objectives
- Evaluate numerical expressions.
- Use parentheses when writing expressions.
- Use the order of operations conventions.
Evaluate the Expression
Lesson Guide
Review use of the multiplication dot instead of the multiplication sign to indicate multiplication.
Have students evaluate the expression 4 ⋅ 6 ÷ 1 + 1 − 1 + 5 ⋅ 2. Write the values students find on the board.
Ask students: Why do you think we got so many different answers?
Let students know that in this lesson, they are going to come up with ways to avoid getting more than one value when evaluating a numerical expression.
If students do not come up with more than one answer, show them the following variations:
Calculating from left to right (ignoring order of operations):
4 · 6 = 24 24 ÷ 1 = 24 24 + 1 = 25 25 – 1 = 24 24 + 5 = 29 29 · 2 = 58
Following the order of operations:
24 + 1 − 1 + 10 = 34
Opening
Evaluate the Expression
Sometimes a dot is used to indicate multiplication rather than the times sign (“×”).
For example, you can write 4 × 3 as 4 · 3. Both of these expressions say to multiply 4 by 3.
- Evaluate the following expression: 4 · 6 ÷ 1 + 1 − 1 + 5 · 2
Math Mission
Lesson Guide
Discuss the Math Mission. Students will look at two different methods for evaluating numerical expressions and come up with a convention so that all expressions are evaluated the same way.
Opening
Explain how an expression can be written so that it is clear which operations should be performed first.
Analyze Jason’s and Denzel’s Calculators
Lesson Guide
Have students work in pairs. As they work, help students think through the problems by asking questions:
- In what order are Jason and Denzel doing the operations?
- Which operation does Jason do first? Is it always the same operation?
- Which operation does Denzel do first? Is it always the same operation?
ELL: Present the questions asked in writing to support ELLs.
When eliciting student explanations, be cognizant of the difficulties some ELLs encounter when they have to express themselves in a language other than their primary language. For example, if you hear them say the right things but use the wrong grammar structure, show signs of agreement in terms of content and softly rephrase using the correct grammar and the student’s words as much as possible.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Some students may struggle to figure out how the calculators operate. Look for students who stick with the problem and try different ways of evaluating the expressions to achieve the given results.
Mathematical Practice 7: Look for and make use of structure.
Identify students who understand the order of the calculations and can generate rules for both calculators. Students may grapple with the use of parentheses in the second set of problems. Listen for students who reason that parentheses indicate that the operations within the parentheses should be done first.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What are you trying to find?
- What patterns do you notice in the calculators’ results?
- How do you describe the order in which the operations are performed?
Student has a solution.
- Explain your strategy for identifying how the different calculators worked.
- Why did you approach the problem in the way that you did?
Answers
- The reason Jason and Denzel got different results from their calculators is that their calculators performed the operations in each expression in a different order. Jason’s calculator performed the operations from left to right. Denzel’s calculator seems to have multiplied and divided before adding and subtracting.
Work Time
Analyze Jason’s and Denzel’s Calculators
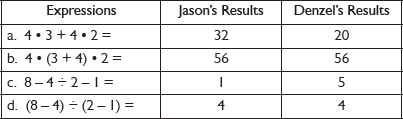
Jason and Denzel use different calculators to find the values of the expressions in this table.
They each get different results from their calculators.
- Why do you think this is happening? What are the two calculators doing differently?
Perform the operations from left to right. Then perform the operations in a different order.
Jason’s and Denzel’s Calculators
Mathematical Practices
Mathematical Practice 7: Look for and make use of structure.
Identify students who understand the order of the calculations and can generate rules for both calculators.
Students may grapple with the use of parentheses in the second set of problems.
Listen for students who reason that parentheses indicate that the operations within the parentheses should be done first.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What are you trying to find?
- What patterns do you notice in the calculators’ results?
- How do you describe the order in which the operations are performed?
- What do you think the parentheses mean in the expressions?
Student has a solution.
- Explain your strategy for identifying how the different calculators worked.
- Why did you approach the problem in the way that you did?
- How did you determine what the parentheses meant in the expressions?
- Why do you think it is important to use parentheses?
- If an expression with more than one operation does not have parentheses, what rules can you give so that the expression has only one value?
Answer
- In the second and fourth table rows, the expressions have parentheses that indicate the order of operations, so Denzel’s and Jason’s calculators will show the same results. In the first and third table rows, the expressions do not have parentheses to indicate the order of operations, so Denzel’s and Jason’s calculators will show different results.
Work Time
Jason’s and Denzel’s Calculators
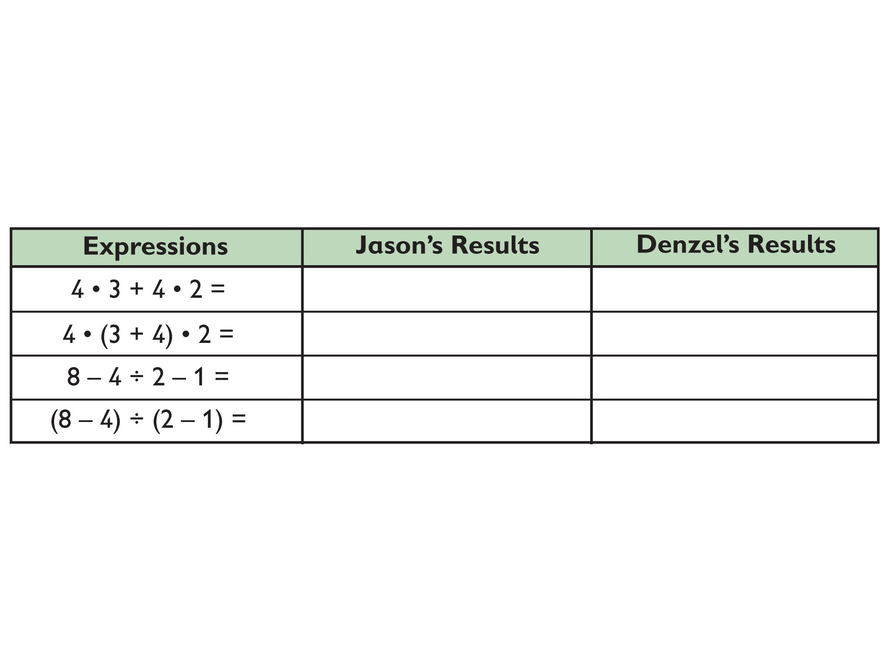
- What do you think Jason’s and Denzel’s calculators will show for the values of the following expressions? Copy and complete the table.
4 · 3 + 4 · 2
4 · (3 + 4) · 2
8 − 4 ÷ 2 − 1
(8 − 4) ÷ (2 − 1)
Hint:
For both calculators, perform the operations in parentheses first.
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who seem to understand how Jason’s calculator works and how Denzel’s calculator works. Also look for students who do not figure out how the two calculators work.
Challenge Problem
Answers
Answers will vary. Possible answer: Expression: 6 ⋅ 5 + 4 ⋅ 2
Jason’s result: 6 ⋅ 5 + 4 ⋅ 2 = 68
Denzel’s result: 6 ⋅ 5 + 4 ⋅ 2 = 38
Work Time
Prepare a Presentation
- State the rules that Jason’s calculator uses and the rules that Denzel’s calculator uses.
- Explain how you evaluated the expressions using the rules from Jason’s calculator and the rules from Denzel’s calculator.
- Explain why you got different answers for the same expressions.
Challenge Problem
- Write an expression that involves more than one operation. Then evaluate it the way Jason’s calculator would solve it and the way Denzel’s calculator would solve it.
Make Connections
Mathematics
Have students share how they think each calculator works. Elicit the following points; however, do not force the discussion. It is important for students to explore their ideas about how the calculators work and then reach conclusions about which ideas are correct and which are not.
- How do Jason’s and Denzel’s calculators work?
- Do you agree with [Name]’s explanation? Does anyone have a different idea?
- What does the use of parentheses in an expression mean?
- Do you think it is okay to get two different values for the same expression? Explain your thinking.
- What rules should there be for how to evaluate an expression so that it has just one value?
- Do you agree with [Name]’s rules? Why or why not?
Explain that if you want to be sure that 8 + 4 is calculated first in the expression 8 + 4 ⋅ 2, then you put parentheses around the 8 + 4 to get (8 + 4) ⋅ 2 = 24. If students have calculators with parentheses keys, let them enter the equation with and without parentheses and compare the results.
Tell students that in algebra, parentheses specify the order in which to evaluate parts of an expression. Explain that when they use parentheses in expressions, there will be no question about the order of the operations. The operations inside parentheses are done first. If an expression has nested parentheses, the operations in the innermost parentheses are evaluated first.
Tell students that if they see an expression that does not have parentheses, they can use the following conventions that mathematicians have agreed on. Outside of parentheses, multiplication and division operations should be done (working from left to right) before addition and subtraction operations.
Thus, the order of operations is as follows:
- Operations inside parentheses first
- Exponents
- Then multiplication and division, working from left to right
- Then addition and subtraction, working from left to right
Avoid acronyms such as PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) because they are misleading. PEMDAS leads to errors such as 8 − 3 + 4 = 8 − 7 = 1, because it suggests that the addition should be done before the subtraction.
ELL: Show these questions in writing and consider providing sentence frames such as:
- I think Jason’s calculator _____
- When I see parentheses in an expression, it means _____
Post these sentence frames as a reference for future lessons.
Performance Task
Ways of Thinking: Make Connections
Takes notes about your classmates’ explanations of the rule for each calculator and their ideas about why the same expression can yield different results.
Hint:
As your classmates present, ask questions such as:
- How did you figure out the rule for each calculator?
- I notice that your explanation about the calculator rules is different from [insert name]’s. Why do you think that is?
- Can you explain how you used the two different rules to evaluate the expressions? What did you do differently when using one rule versus the other?
- Do you think it is okay to get two different values for the same expression? Why or why not?
Evaluate Expressions
Lesson Guide
Ask questions such as the following as students are working:
- How did you get that answer?
- Which operation will you perform first in this expression? Why?
- What operation does the fraction indicate?
- What do the parentheses mean?
Answers
- 2(25 + 20) − 3 = 2(45) − 3 = 90 − 3 = 87
- 2 + − 3 = 2 + 3 − 3 = 2
- (2 + 15)(15 − 5) = 17 ⋅ 10 = 170
- 3 ⋅ 22 = 3 ⋅ 4 = 12
Work Time
Evaluate Expressions
When you evaluate numerical expressions, perform operations in this order:
- Operations inside parentheses
- Exponents
- Multiplication and division, working from left to right
- Addition and subtraction, working from left to right
When you write numerical expressions, use parentheses to show which operation(s) should be performed first.
Evaluate these expressions:
- 2(25 + 20) − 3
- 2 + 6 ÷ 2 − 3
- (2 + 15)(15 − 5)
- 3 ⋅ 22
Evaluate Numerical Expressions
A Possible Summary
It is best to use parentheses when writing expressions to show the order of operations. You can use the following conventions for the order of performing the operations:
- Operations inside parentheses first
- Exponents
- Then multiplication and division, working from left to right
- Then addition and subtraction, working from left to right
SWD: Clearly summarize the lesson, and write down all salient information. Make sure students are recording Summary of Math notes in their Notebook.
Additional Discussion Points
- If there are nested parentheses, the operations in the innermost parentheses are evaluated first.
- Understanding the use of parentheses is especially important when interpreting the associative and the distributive properties.
Formative Assessment
Summary of the Math: Evaluate Numerical Expressions
Write a summary of what you learned about evaluating numerical expressions.
Hint:
Check your summary.
- Does your summary explain why parentheses are used in expressions?
- Does your summary explain how to evaluate an expression if it does not have parentheses?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to learn what students understand about the role of parentheses in expressions.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Parentheses are useful in writing expressions because …