- Author:
- Chris Adcock
- Subject:
- Algebra, Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Distributive Properties of Geometric Models

Overview
Students use a rectangular area model to understand the distributive property. They watch a video to find how to express the area of a rectangle in two different ways. Then they find the area of rectangular garden plots in two ways.
Key Concepts
The distributive property can be used to rewrite an expression as an equivalent expression that is easier to work with. The distributive property states that multiplication distributes over addition.
- Applying multiplication to quantities that have been combined by addition: a(b + c)
- Applying multiplication to each quantity individually, and then adding the products together: ab + ac
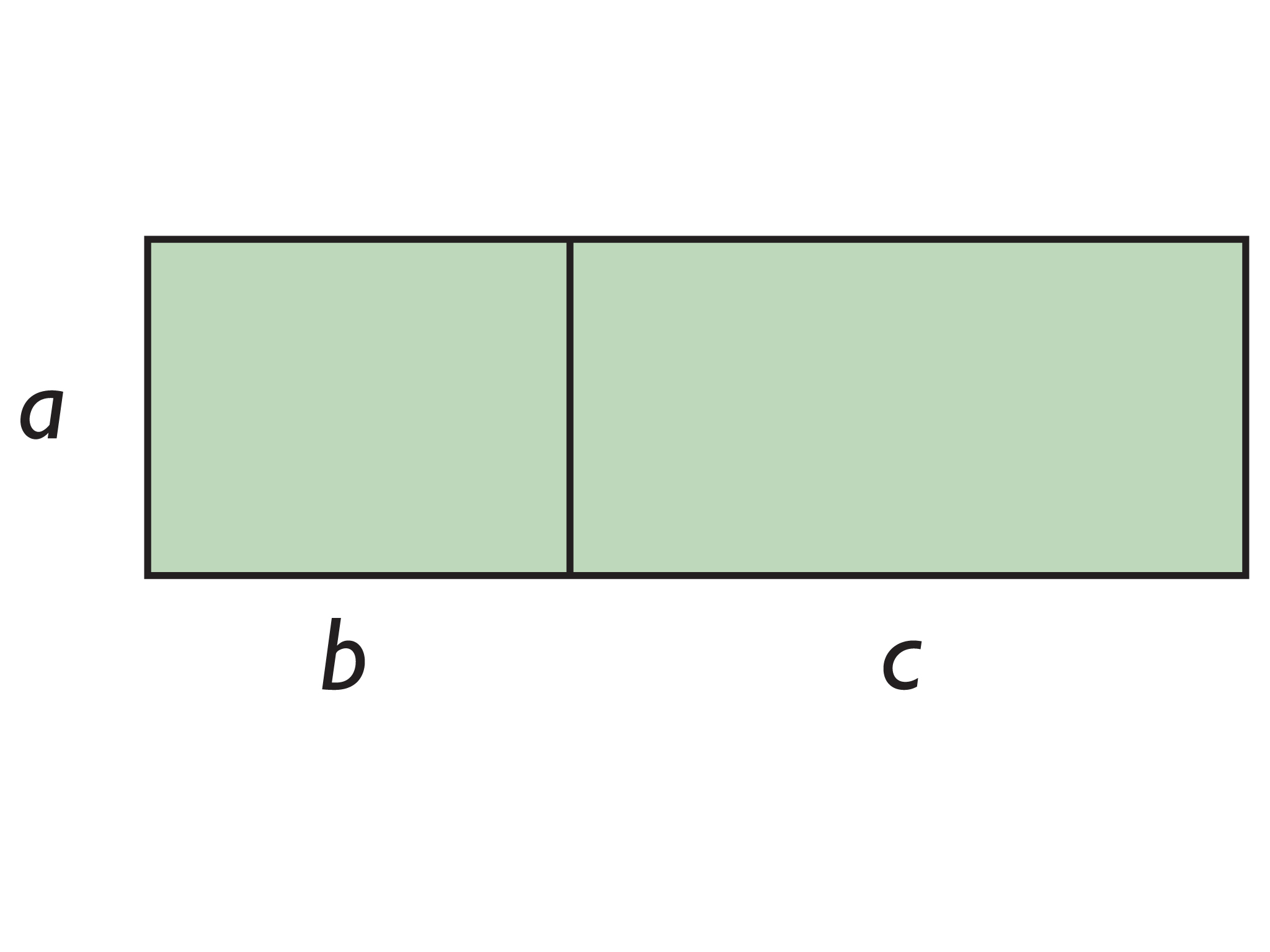
The distributive property can be represented with a geometric model. The area of this rectangle can be found in two ways: a(b + c) or ab + ac. The equality of these two expressions, a(b + c) = ab + ac, is the distributive property.
Goals and Learning Objectives
- Use a geometric model to understand the distributive property.
- Write equivalent expressions using the distributive property.
Area of a Rectangle
Lesson Guide
Students will work in a context that requires activating their prior knowledge of area. Consider a brief discussion about area to ensure all students remember the following:
- Area is the size of the region enclosed by a figure, expressed in square units.
Begin by having students watch the video. Students may need to watch it more than once. Tell students to pay close attention to the different ways to express the area.
Have students think about how to write two expressions for the area of the rectangle in the image on the student screen.
Give students a chance to share ideas. Choose one or two student responses to share with the class.
- The two correct expressions are ab + ac and a(b + c). The equality of these two expressions is an example of the distributive property of multiplication over addition.
ELL: When showing the video, monitor that ELLs are following the meaning of what is presented. If necessary, pause the video and allow them to ask clarifying questions. Alternatively, ask questions to check for understanding of what they are watching.
Opening
Area of a Rectangle
- Watch the video about finding ways to express the area of a rectangle when the length and width are unknown.
- Write two expressions for the area of this rectangle.
VIDEO: Area of Rectangle
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find the area of rectangular garden plots in two ways using the distributive property.
Opening
Write two equivalent expressions and show they are equivalent using the distributive property.
Garden Plots
Lesson Guide
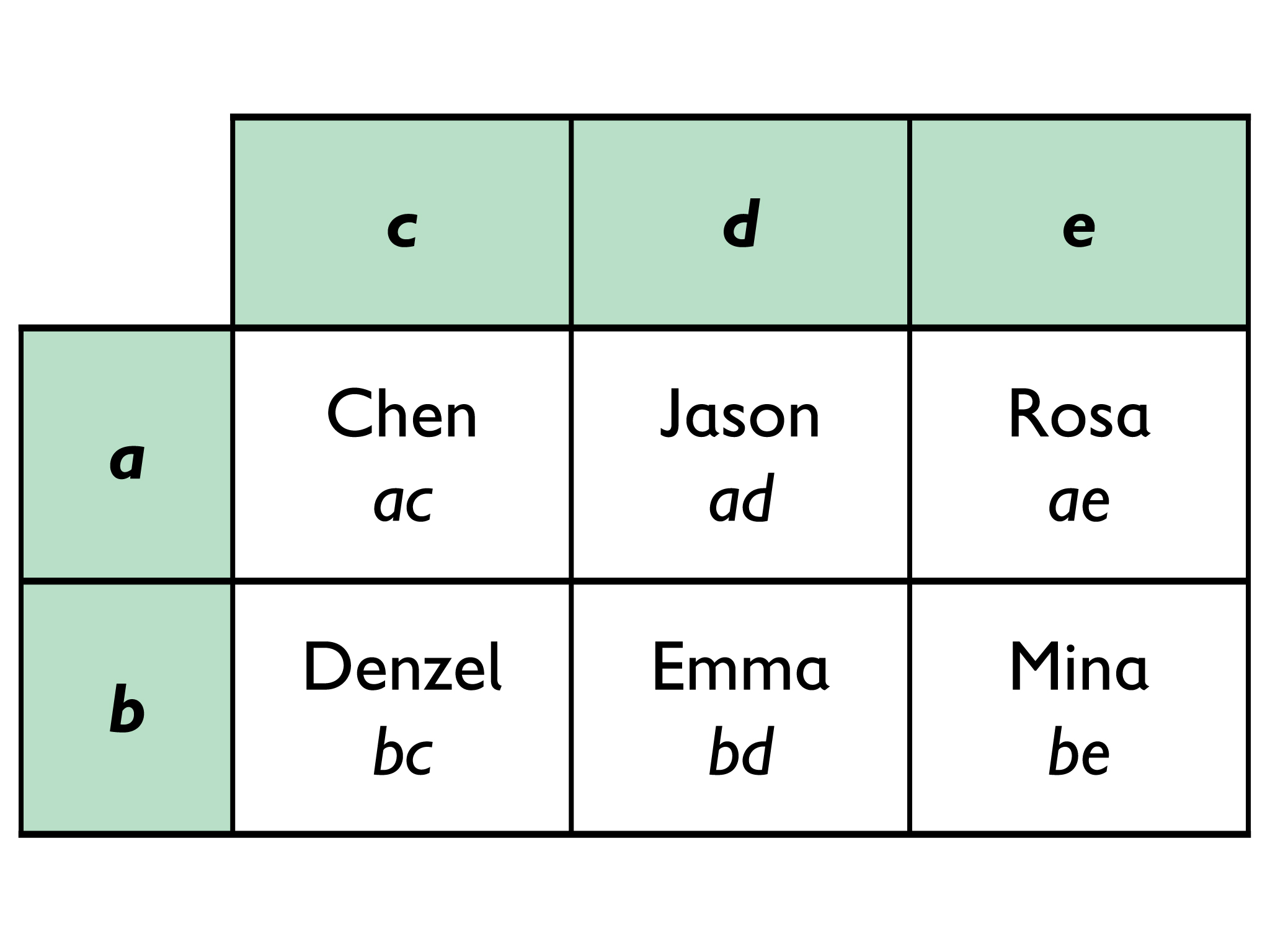
Sketching the garden requires that students pay close attention to the dimensions of each plot and that they keep in mind that the plots must fit together to form a rectangle. A careful study of the dimensions of each plot reveals that the garden has one side of length a + b and the other side of length c + d + e.
While more than one arrangement of the garden plots is possible, they are all variations of the following sketch:
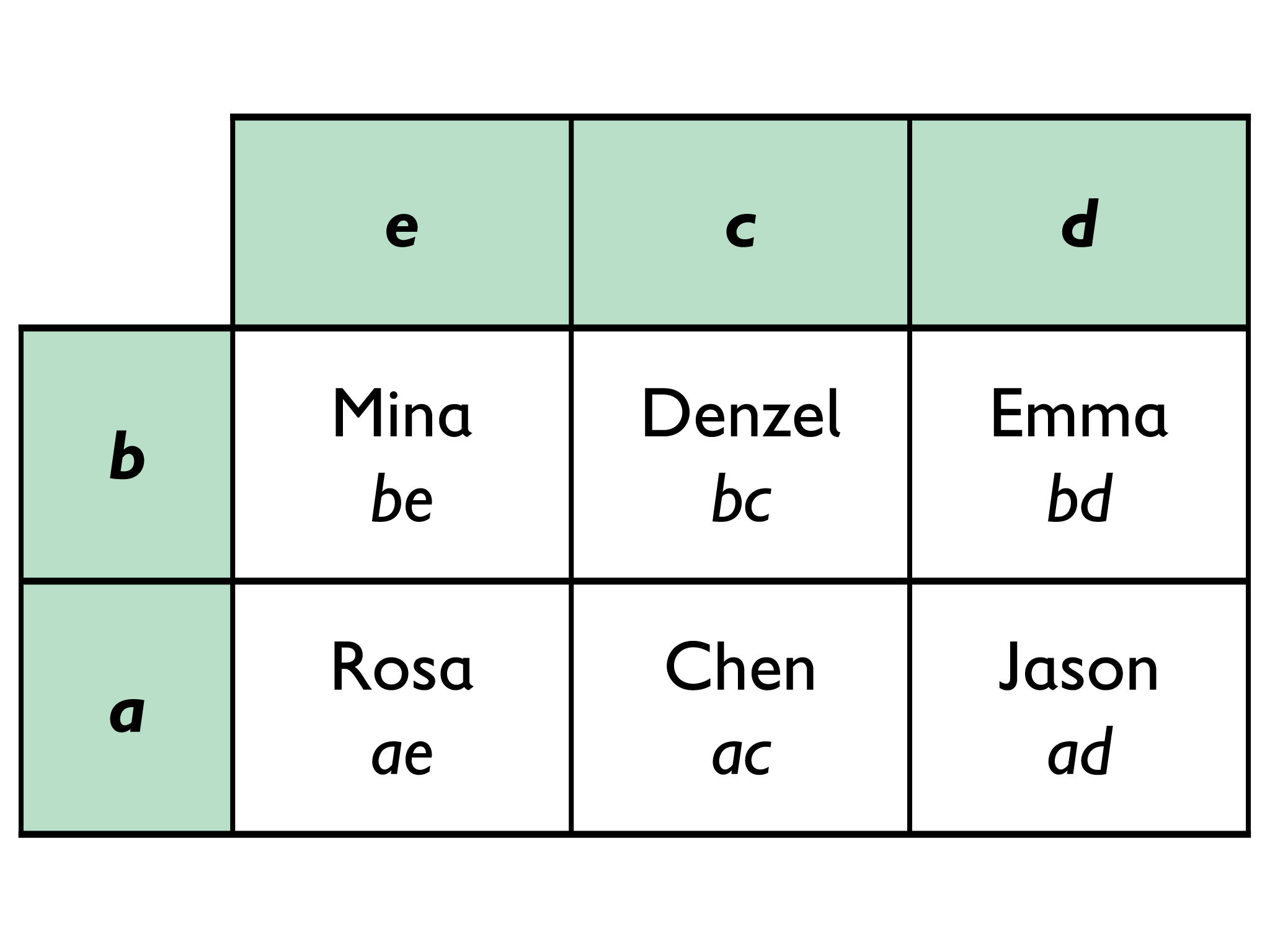
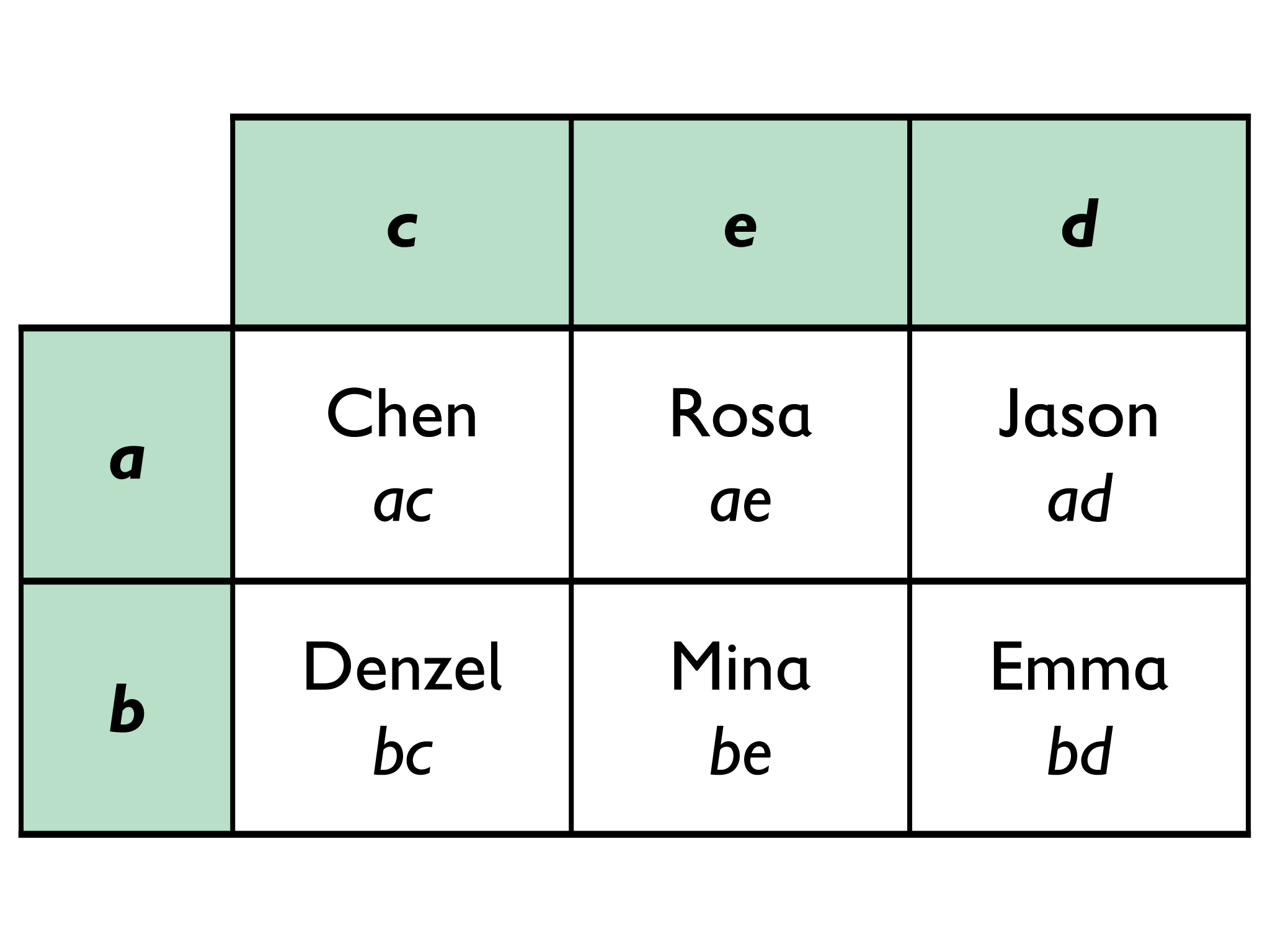
Look for garden arrangements that lend themselves to a discussion of the commutative property. For example, these arrangements:
SWD: Provide concrete models like labeled paper cutouts of the six garden plots for students with a tactile learning style. Next, transition learners from their concrete models to their garden sketches. Finally, guide students to the abstract by having them express the garden plots using the distributive property.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
Students must sketch the garden plots precisely to represent the location of each person’s plot based on the descriptions given. Look for students who have trouble figuring out what to sketch.
Mathematical Practice 4: Model with mathematics.
As students work, watch for students who are correctly using the rectangular garden plot to model the distributive property.
Mathematical Practice 7: Look for and make use of structure.
Look for students who use the distributive property correctly to write two equivalent expressions for each of the combined areas and for students who do not distribute multiplication over addition correctly.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What shape is the garden? What shape are the six plots?
- What does Denzel’s plot look like? How will you label the length and the width? Show me a sketch.
- Whose plot can go next to Denzel’s plot? Explain how you know.
- Is there another possible solution? Explain your thinking.
- How can you determine the arrangements of the other plots?
Student does not understand the visual representation or model.
- Where do you see the length and the width of each plot in your sketch?
- Where do you see the length and the width of the entire garden in your sketch?
- How can you represent the area of [Denzel’s plot, the garden] as an algebraic expression? Can you represent it in a different way? Show me.
- What is the distributive property? How does this model show the distributive property?
Answer
- Possible sketch of the garden:
Work Time
Garden Plots
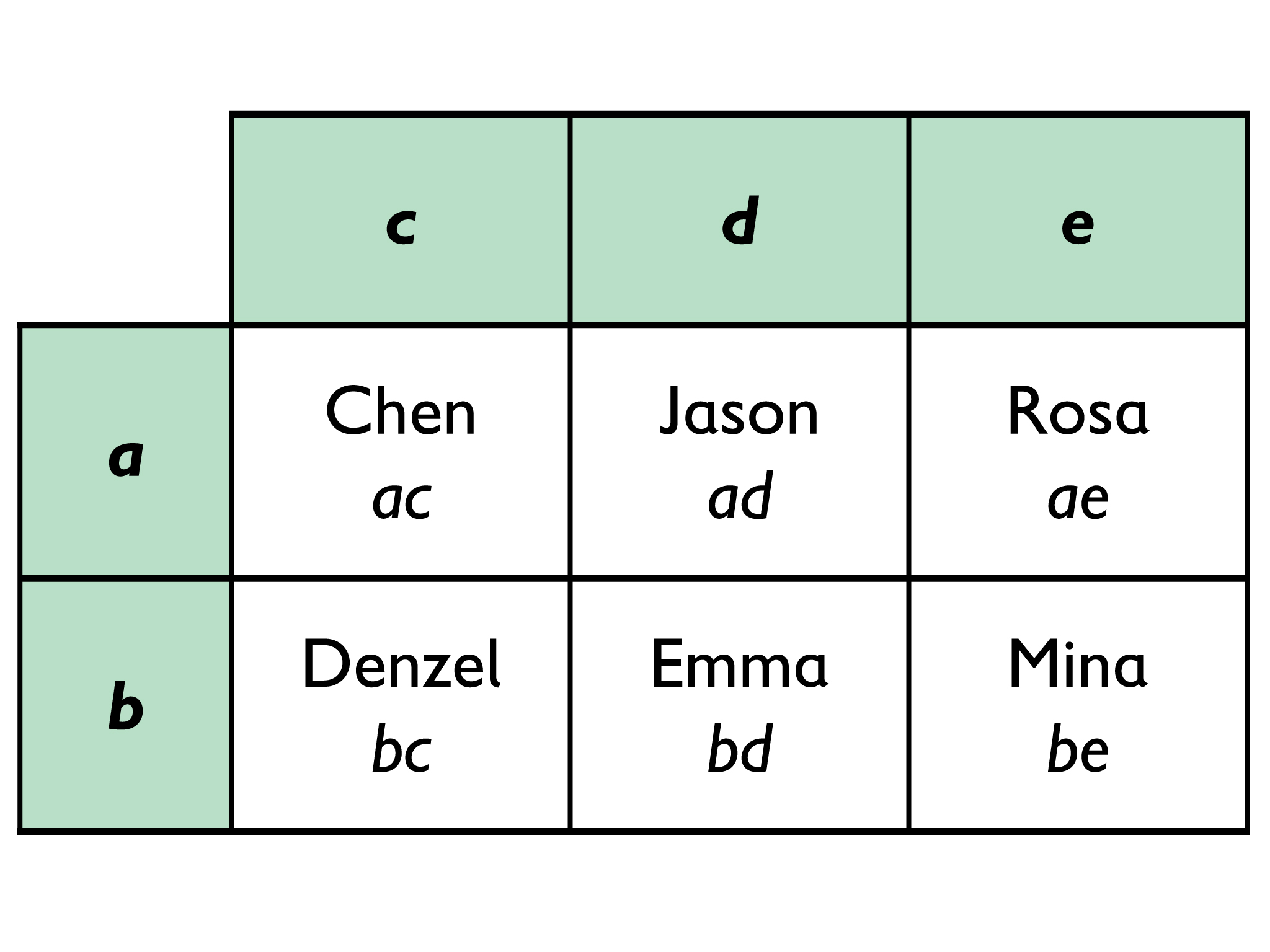
Six students have garden plots of various sizes in a garden. All the plots are rectangles and the garden itself is a rectangle.
Denzel’s plot has an area of bc.
Mina’s plot has an area of be.
Jason’s plot has an area of ad.
Rosa’s plot has an area of ae.
Chen’s plot has an area of ac.
Emma’s plot has an area of bd.
- Make a sketch showing how the garden might be divided. Label each plot with the name of the student who is in charge of the plot, followed by the area of the plot.
Hint:
- Start by drawing Denzel’s garden plot. Label the length b and the width c.
- Whose plot can you draw next to his?
Area of Garden Plots
Mathematics
[common error] You may notice that some students write c(a + b) and ca + b for the area of Denzel’s plot after Chen gives his plot away, because they fail to distribute multiplication over all the addends. If you see this common error, note it for discussion in Ways of Thinking.
Possible Answers
- If Chen gives Denzel his plot, the area of Denzel’s new plot will be c(a + b) or ca + cb (or ac + bc).
- If Chen keeps his plot but Emma and Mina give Denzel their plots, the area of Denzel’s new plot will be b(c + d + e) or bc + bd + be.
- The area of the entire garden is (a + b)(c + d + e) or ac + ad + ae + bc + bd + be.
Work Time
Area of Garden Plots
For each of these problems, write two expressions. Use your garden diagram and the distributive property to show that your expressions are equivalent.
- If Chen gives Denzel his plot, what will the area of Denzel’s new plot be?
- If Chen keeps his plot but Emma and Mina give Denzel their plots, what will the area of Denzel’s new plot be?
- What is the area of the entire garden?
Hint:
- Look at your sketch of the garden. Outline the area of Denzel’s new plot after he gets Chen’s plot. What is the length and width of Denzel’s new plot?
- Look at your sketch of the garden. Find Denzel’s original plot. Add the areas of Emma’s and Mina’s plots. What is the length and width of Denzel’s plot now?
- What expression represents the length of the entire garden? What expression represents the width of the entire garden?
Prepare a Presentation
Preparing for Ways of Thinking
Be sure students explain how they wrote the two expressions for each area and how they used the distributive property to show that the two expressions are equivalent.
Challenge Problem
Possible Answers
- Problems will vary.
- Answers will vary.
Work Time
Prepare a Presentation
- Explain how you wrote the two expressions for each area.
- Explain how you used the distributive property, a(b + c) = ab + ac, to show that the two expressions are equivalent.
Challenge Problem
- Write a problem that involves area and the distributive property, and find the solution.
- Then exchange problems with a partner and solve each other’s problems.
Make Connections
Lesson Guide
Have students give their presentations. The goal here is for students to apply their understanding of the properties of operations (especially the distributive property) to write equivalent expressions. Identify student work that shows how the properties work together to make equivalent expressions. Ask students:
- What strategies did you use to sketch the garden?
- Compare [Name]’s garden sketch and [Name]’s garden sketch. Are they both correct representations of the garden? Explain how you know.
- Explain how the two expressions you wrote to represent the area of Denzel’s new garden plot are equivalent:
- Where do you see this in your sketch?
- What properties did you use? Where do you see this in your work?
- How does this model represent the distributive property?
ELL: Create a written summary of the mathematics from the presentations. Make sure all students have recorded information in their notes.
Performance Task
Ways of Thinking: Make Connections
Takes notes about your classmates’ approaches to solving the problems.
Hint:
As your classmates present, ask questions such as:
- What strategy did you use to sketch the garden?
- How does your sketch of the garden compare to those of your classmates?
- Is there only one correct garden sketch? Explain.
- How do your two expressions represent the area of
this plot? - Where do you see the length of the plot in the sketch? Where do you see the width?
- How is the distributive property represented in your garden sketch?
Expressions and Properties of Operations
Mathematics
- Have pairs quietly discuss the distributive property and how the rectangle shown is a geometric model of it.
- As student pairs work together, listen for students who may still have difficulty understanding how the distributive property is represented by the geometric model. Work with these students individually or in pairs to clarify any misunderstandings.
- Then discuss the distributive property as a class. Be sure to highlight these points:
- The distributive property says that multiplication distributes over addition.
- Applying multiplication to quantities that have been combined by addition: a(b + c)
- Applying multiplication to each quantity individually and then adding the products together: ab + ac
- The distributive property says that multiplication distributes over addition.
This rectangle is a geometric model of the distributive property. The area of the rectangle can be found in two ways: a(b + c) or ab + ac. The equality of these expressions, a(b + c) = ab + ac, is the distributive property.
Formative Assessment
Summary of the Math: Expressions and Properties of Operations
Read and Discuss
- The distributive property enables you to rewrite an expression as an equivalent expression.
- It works for algebraic expressions in exactly the same way that it works for whole numbers. You have already used the distributive property to help you make mental math calculations, such as determining that: 12 · 32 = 10 · 32 + 2 · 32.
- With algebraic expressions, the distributive property works the same way: a(b + c) = ab + ac
- This rectangle is a geometric model of the distributive property. The area of the rectangle can be found using two different expressions: a(b + c) or ab + ac. The equality of these expressions, a(b + c) = ab + ac, is the distributive property.
Hint:
Can you:
- Explain the distributive property?
- Show how to represent the distributive property using a visual model?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out why students like using the distributive property.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I like using the distributive property because …