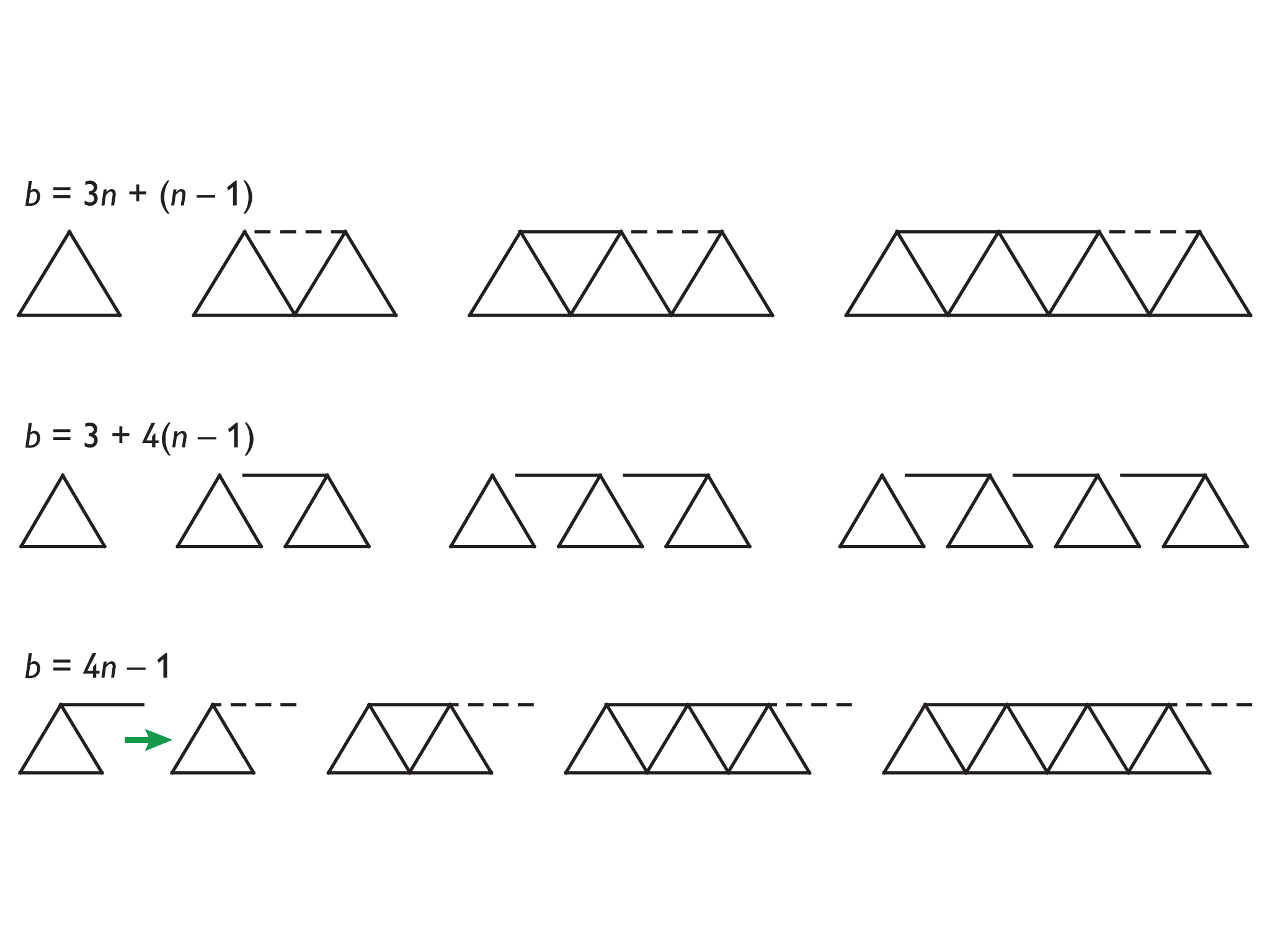- Author:
- Chris Adcock
- Subject:
- Mathematics
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Matching Words and Expressions
Gallery Problems Exercise

Overview
Lesson Guide
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery Descriptions
Building Bridges
Students will examine a pattern and use expressions to show how to continue the pattern.
Patterns in a Table
Students will complete a table by noticing relationships within the table and using those relationships to fill in empty cells in the table.
Expressions for Perimeter and Area
Students will write equivalent expressions for the perimeters and areas of various rectangles.
Multiplication Table
Students will complete an unusual multiplication table by writing the algebraic expression that results from multiplying the terms given in the top row by the ones given in the left column.
Garden Beds
Students will find the number of square tiles needed to pave around various configurations of rectangular garden beds. Then, students will write an algebraic equation to represent the number of square tiles needed to go around any number of plants in a single row.
Telephone Tree
Students will solve problems about a telephone tree and use expressions to show the number of calls completed after a given number of rounds of calling.
Stacks of DVDs
Students will write an expression to describe the width of a stack of DVDs, and then they will evaluate the expression for different numbers of DVD cases and boxed sets.
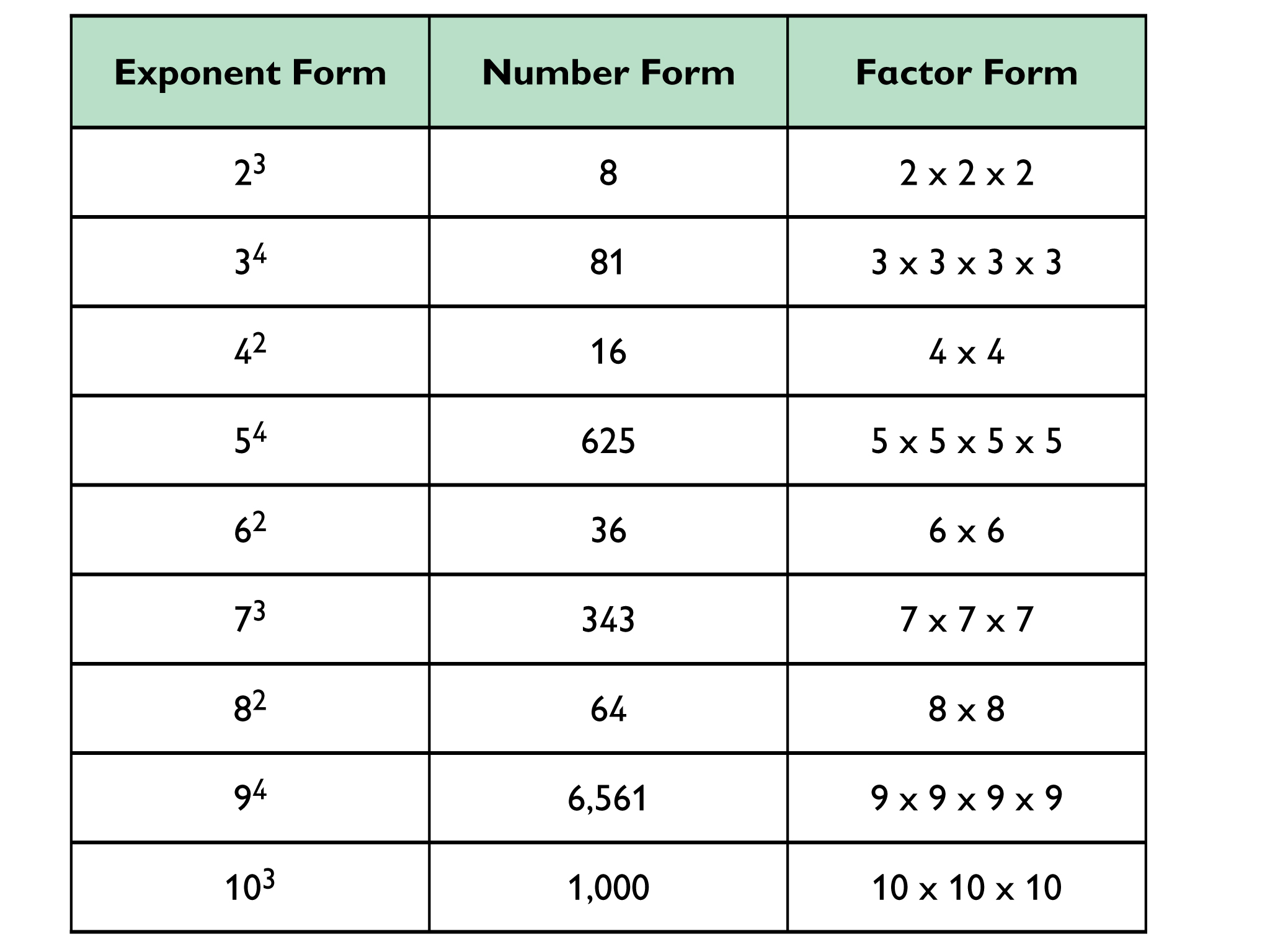
Exponent Card Sort
Students will complete a card sort that will give them practice working with exponents. Then they will use a set of blank cards to complete sets that purposely have one or two representations missing.
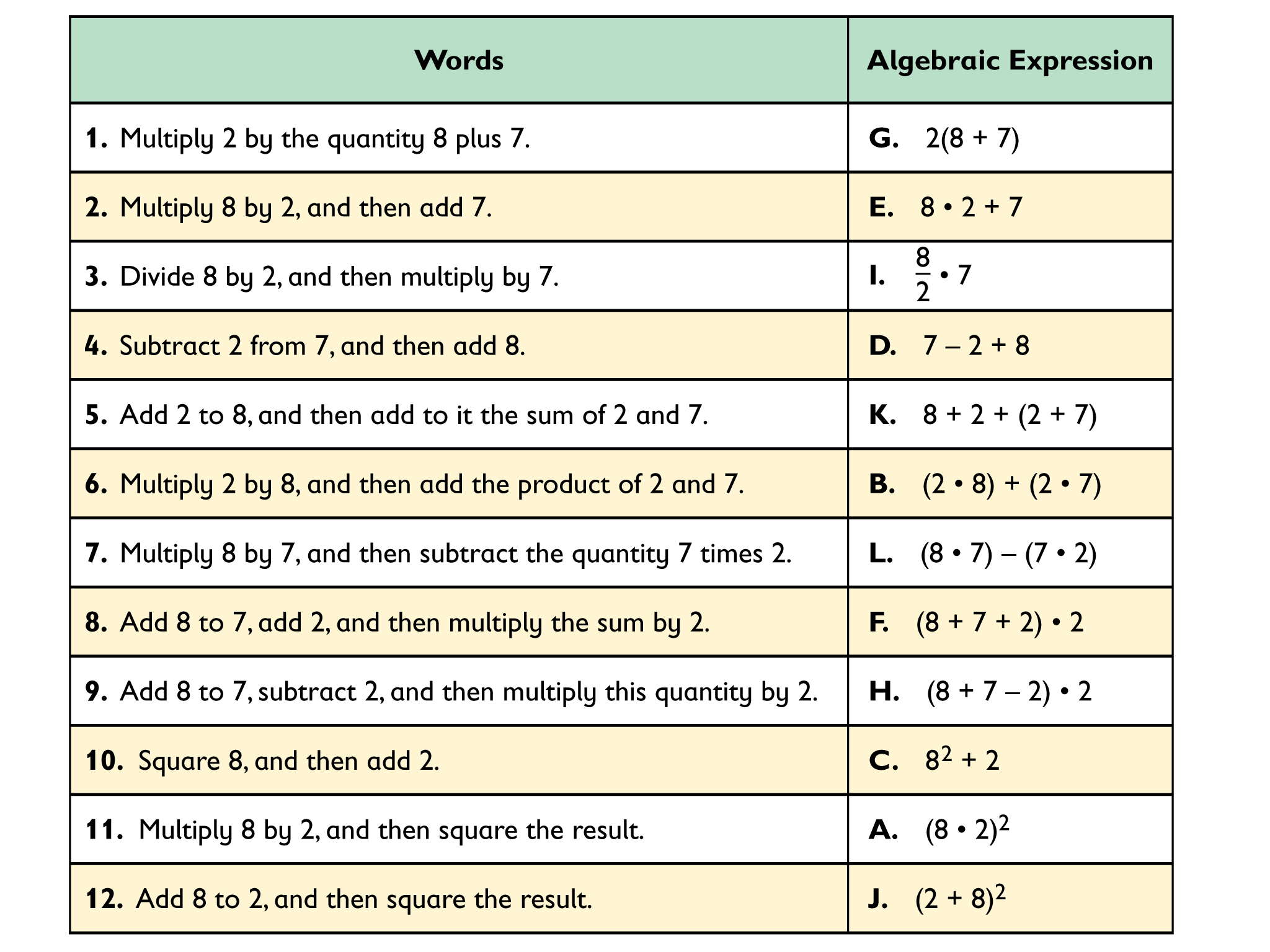
Matching Words and Expressions
Students will match a verbal statement with its expression in this card sort.
Investigating Factors and Multiples
Students will investigate an interesting property of numbers involving the greatest common factor and the least common multiple.
Fourth Rock
Students will solve a problem about how long it will take for two imaginary planets in an imaginary solar system to align so that they are at their closest distance from each other.
Factors of a Number
Students will decide whether a mathematical claim about factors and multiples is true or false based on given criteria.
Common Factors
Students will look at two unknown numbers with a greatest common factor of 20 and determine what other factors must be common to the two unknown numbers. Students will use their answer to make a generalization.
History of Variables
Students will research the history of variables. When were they first used? Where were they first used? Who used them?
Create a Video
Students will use their creative powers to produce a video about expressions.
Building Bridges
Answers
Explanations will vary. Students should state that the expressions are all equivalent because they all represent the same situation.
Opening
Work Time
Building Bridges
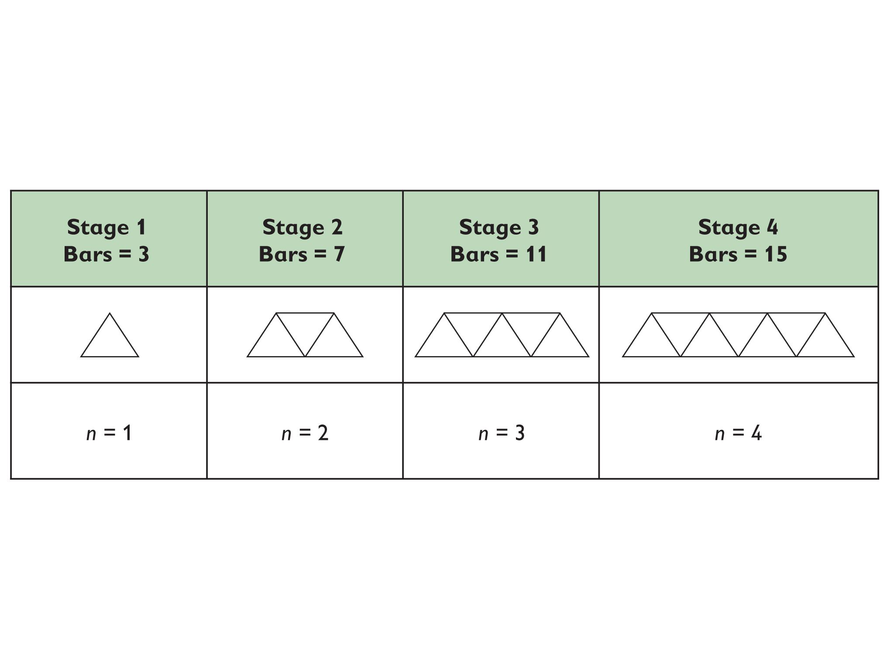
The diagrams in this table represent a series of bridges. The bars are the segments that make up a bridge. n represents the number of triangles. b represents the number of bars.
The following algebraic expressions show different ways to calculate the number of bars based on the number of triangles.
b = 3 + 4(n – 1)
b = 3n + (n – 1)
b = 4n – 1
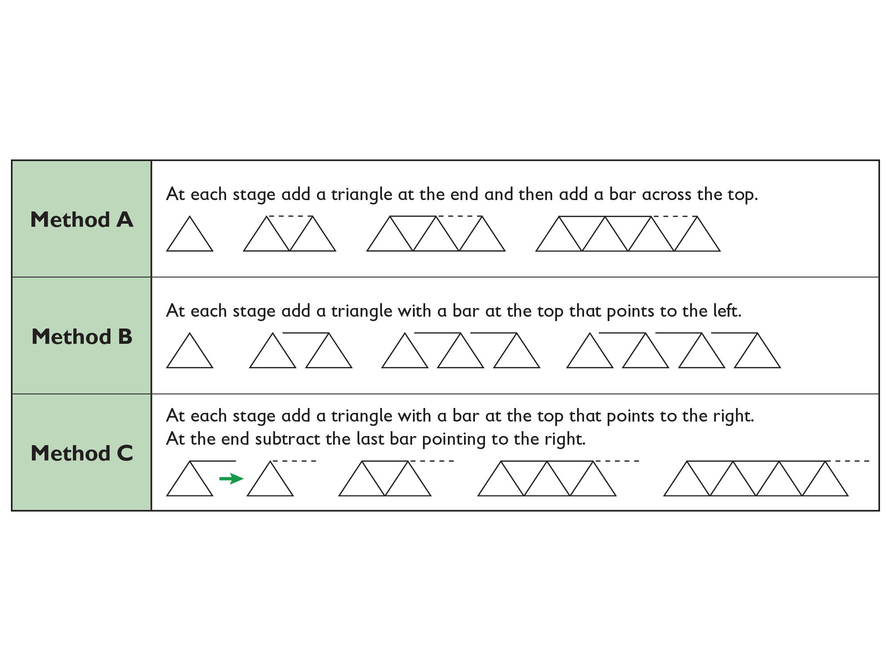
Each expression was found based on a different method for constructing the bridges. These methods are explained and illustrated here.
Method A: At each stage add a triangle at the end and then add a bar across the top.
Method B: At each stage (after the first stage) add a triangle with a bar at the top that points to the left.
Method C: At each stage add a triangle with a bar at the top that points to the right. At the end subtract the last bar pointing to the right.
- Determine which expression matches which method/diagram.
- Evaluate each expression for n = 10.
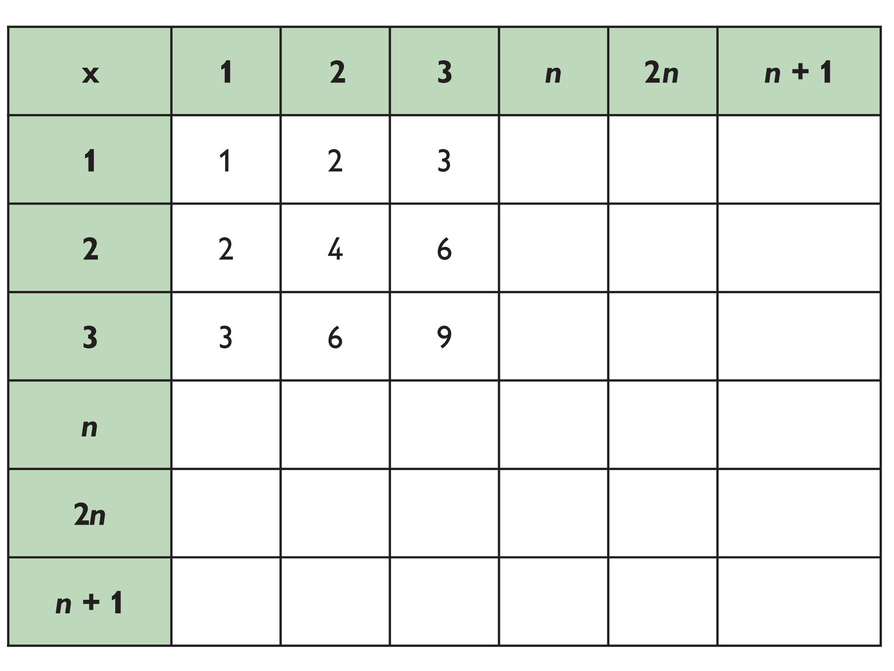
Patterns in a Table
Answers
Work Time
Patterns in a Table
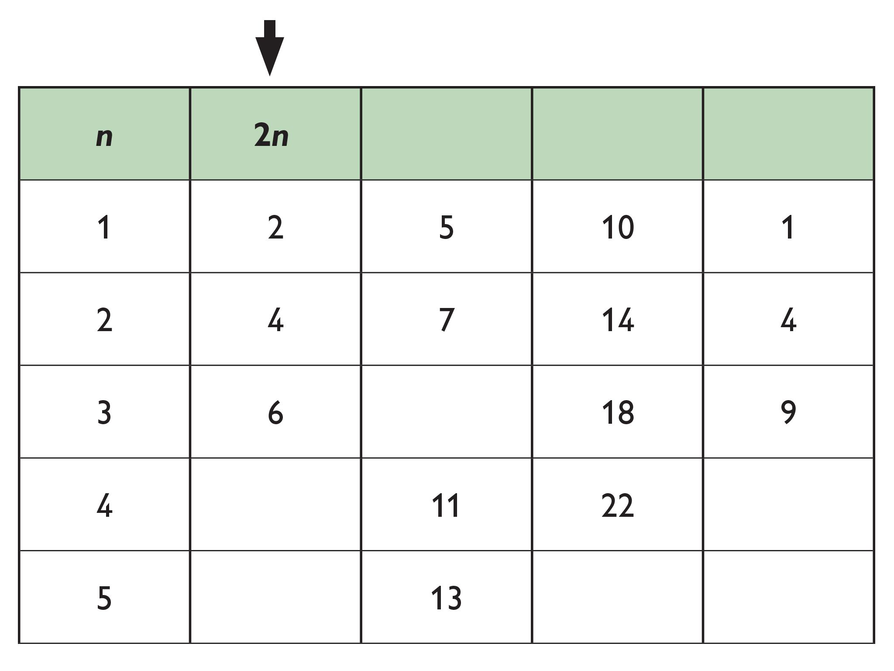
- Complete the table. In the top row of each column write an expression that relates the values for n. For example, the numbers in the second column are all two times the numbers in the first column, so the heading for the second column is 2n.
- Then evaluate the expression you wrote in the top row, using the values in the first column, to fill in any empty cells in that column.
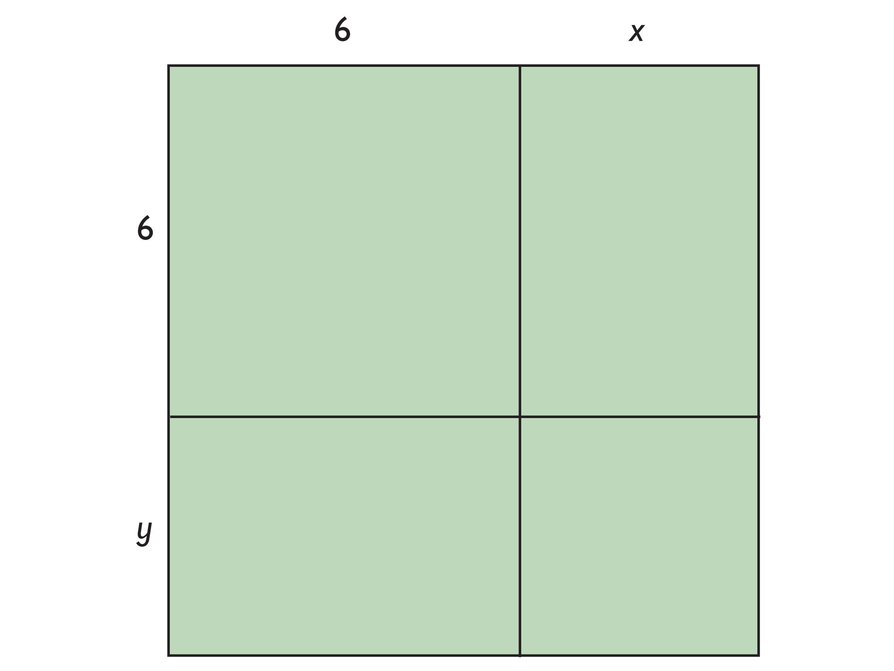
Expressions for Perimeter and Area
Answers
Figure 1
Possible answers:
Perimeter:
(6 + 4) + (6 + 4) + (6 + 4) + (6 + 4)
4(6 + 4)
4 ⋅ 6 + 4 ⋅ 4
4 ⋅ 10
The perimeter is 40 units.
Area
(6 + 4)(6 + 4)
6 ⋅ 6 + 6 ⋅ 4 + 4 ⋅ 6 + 4 ⋅ 4
6(6 + 4) + 4(6 + 4)
6 ⋅ 10 + 4 ⋅ 10
10 ⋅ 10
The area is 100 square units.
Figure 2
Possible answers:
Perimeter
(6 + x) + (6 + x) + (6 + x) + (6 + x)
4(6 + x)
4 ⋅ 6 + 4⋅x
The perimeter is 4x + 24 units.
Area
(6 + x)(6 + x)
(6 + x)2
6 ⋅ 6 + 6 ⋅ x + x ⋅ 6 + x ⋅ x
6(6 + x) + x(6 + x)
The area is x2 + 12x + 36 square units.
Figure 3
Possible answers:
Perimeter
(6 + x) + (6 + x) + (6 + y) + (6 + yy)
2(6 + x) + 2(6 + y)
The perimeter is 2x + 2y + 24 units.
Area
(6 + x)(6 + y)
6(6 + x) + y(6 + x)
6(6 + y) + x(6 + y)
6 ⋅ 6 + 6 ⋅ y + x ⋅ 6 + x ⋅ y
The area is xy + 6x + 6y + 36 square units.
Work Time
Expressions for Perimeter and Area
For each of the figures:
- Write two or more equivalent expressions for the perimeter, and two or more equivalent expressions for the area of each figure.
- Then express the perimeter and area in the simplest form that you can.
Figure 1:
Figure 2:
Figure 3:
Multiplication Table
Answers
Work Time
Multiplication Table
This multiplication table has been started for you.
- Copy and complete the table.
Garden Beds
Answers
100 + 100 + 3 + 3 = 206
For a row of 100 plants, you need 206 square tiles.
n + n + 3 + 3 = 2n + 6
For a row of n plants, you need 2n + 6 square tiles.
Square tiles needed are as follows:
50 + 50 + 4 + 4 = 108
For 2 rows of 50 plants each, you need 108 square tiles.25 + 25 + 6 + 6 = 62
For 4 rows of 25 plants each, you need 62 square tiles.20 + 20 + 7 + 7 = 54
For 5 rows of 20 plants each, you need 54 square tiles.10 + 10 + 12 + 12 = 44
For 10 rows of 10 plants each, you need 44 square tiles.
Note that while the number of plants is the same in each case, the number of square tiles needed to surround them is different.
4. For n rows of m plants you need:
- m square tiles above
- m square tiles below
- n + 2 square tiles to the left
- n + 2 square tiles to the right
m + m + (n + 2) + (n + 2) = 2m + 2(n + 2) = 2m + 2n + 4
Work Time
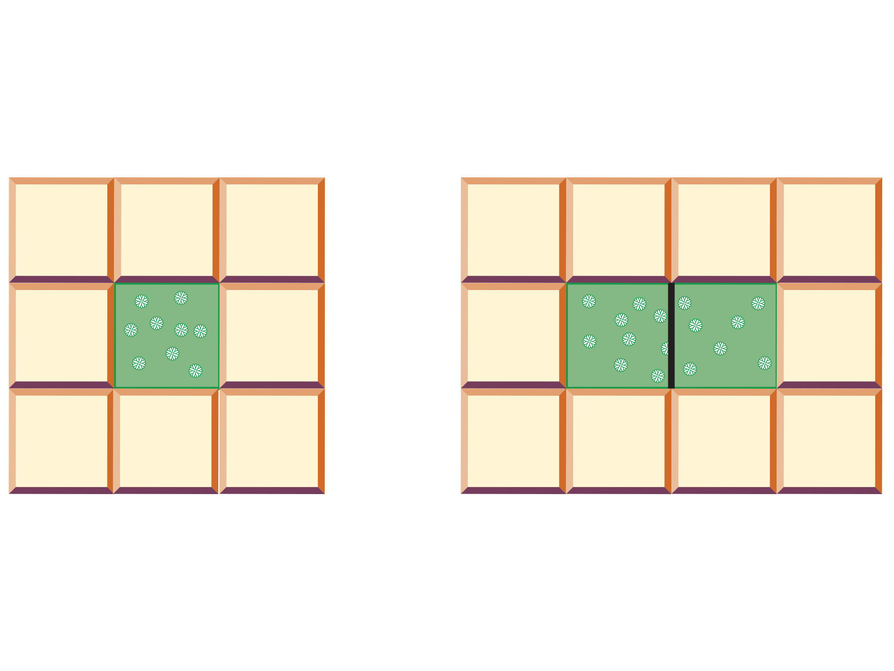
Garden Beds
A garden nursery sells square tiles for making borders around groups of plants (planting beds). The border tiles go only on the outside of all the plants—no tiles go between the plants. In the diagram, the square tiles are represented by tan squares and each plant is represented by 1 green square.
- How many square tiles are needed for 1 row of 100 plants?
- Write an algebraic expression that represents the number of square tiles needed for any number of plants planted in a single row.
- Find how many square tiles are needed for the following planting beds:
- 2 rows of 50 plants
- 4 rows of 25 plants
- 5 rows of 20 plants
- 10 rows of 10 plants
- Use a double number line or look at the relationship between the number of plants and the number of square tiles.
Telephone Tree
Answers
During the first round, there are 3 calls. During the second round, there are 3 ⋅ 3 calls. During the third round, there are 3 ⋅ 3 ⋅ 3 calls. During the fourth round, there are 3 ⋅ 3 ⋅ 3 ⋅ 3 calls. Finally, during the fifth round, there are 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3, or 243, calls made.
During the nth round, there will be 3n calls made.
Work Time
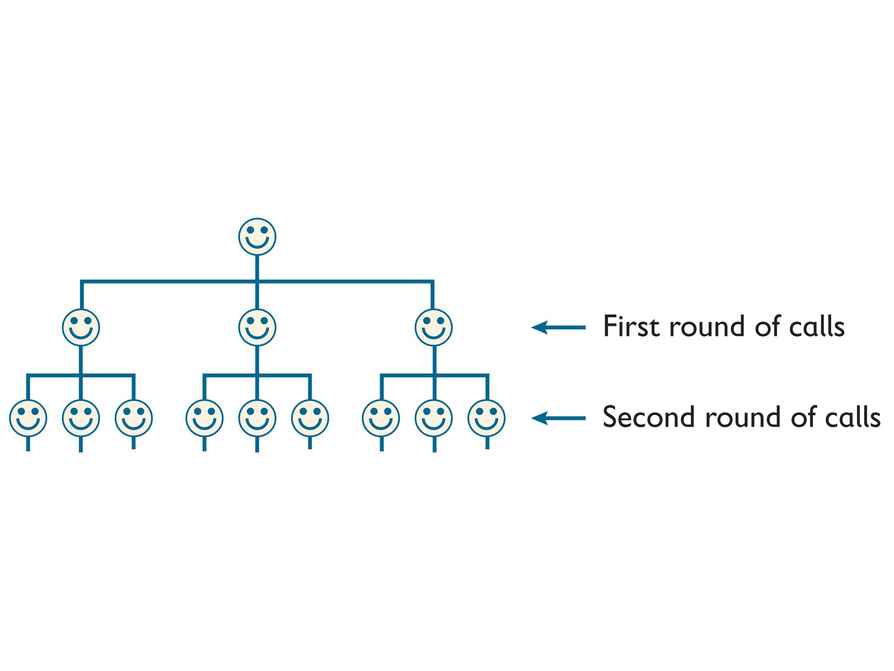
Telephone Tree
A club set up a telephone tree so that all club members can receive important news quickly. The club secretary calls 3 people, and each of those people call 3 people, and so on.
- Finish the telephone tree to show all the calls that will be completed by the third round.
- What expression can be used to show the number of calls made during the fifth round? Evaluate this expression.
- What expression can be used to show the number of calls completed during the nth round?
Stacks of DVDs
Answers
If you use c to represent the number of DVD cases and b to represent the number of boxed sets:
- The width of the stack on the shelf is 14c + 42b millimeters.
- 14(10) + 42(5) = 350
The width of the stack if there are 10 DVD cases and 5 boxed sets is 350 millimeters, or 35 centimeters. - 14(32) + 42(15) = 1,078
The width of the stack if there are 32 DVD cases and 15 boxed sets is 1,078 millimeters, or 1.078 meters.
Work Time
Stacks of DVDs
There are DVD cases and boxed sets of DVDs stacked on a shelf. The DVD cases are 14 millimeters thick and the boxed sets are 42 millimeters thick.
- Write an expression for the width of the stack on the shelf if the numbers of DVD cases and sets of DVDs are unknown.
- What is the width of a stack if there are 10 DVD cases and 5 boxed sets?
- What is the width of a stack if there are 32 DVD cases and 15 boxed sets?
Exponent Card Sort
Answers
Work Time
Exponent Card Sort
Work alone or with a partner on the Exponent Card Sort.
- Match a number and a factor form from the right to each expression form to complete the table.
- Some sets will have a missing form. Use a blank card to write the missing form for that set.
HANDOUT: Exponent Card Sort
Matching Words and Expressions
Answers
Matching Words and Expressions
- Sort the Expression Cards to match the Word Cards.
- When you find a match, explain how you know the cards match.
HANDOUT: Matching Words and Expressions
Investigating Factors and Multiples
Answers
Answers will vary. Possible answer for 36 and 42:
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 42: 1, 2, 3, 6, 7, 14, 26, 42
GCF: 6
Multiples of 36: 36, 72, 108, 144, 180, 216, 252
Multiples of 42: 42, 84, 126, 168, 210, 252
LCM: 25236 × 42 = 1,512
6 × 252 = 1,512
6 × 252 = 1,512 = 36 × 42
2. Answers will vary.
3. Explanations will vary. The product of the two numbers I chose, and the product of their GCF and LCM, give the same result.
Work Time
Investigating Factors and Multiples
- Choose any pair of numbers and follow these steps:
- Find the greatest common factor (GCF) and the lowest common multiple (LCM).
- Find the product of your two original numbers.
- Find the product of the GCF and LCM.
- Compare the two products.
- Choose other pairs of numbers and repeat the steps above.
- What do you notice about the products in each case? How do you explain your results?
Fourth Rock
Answers
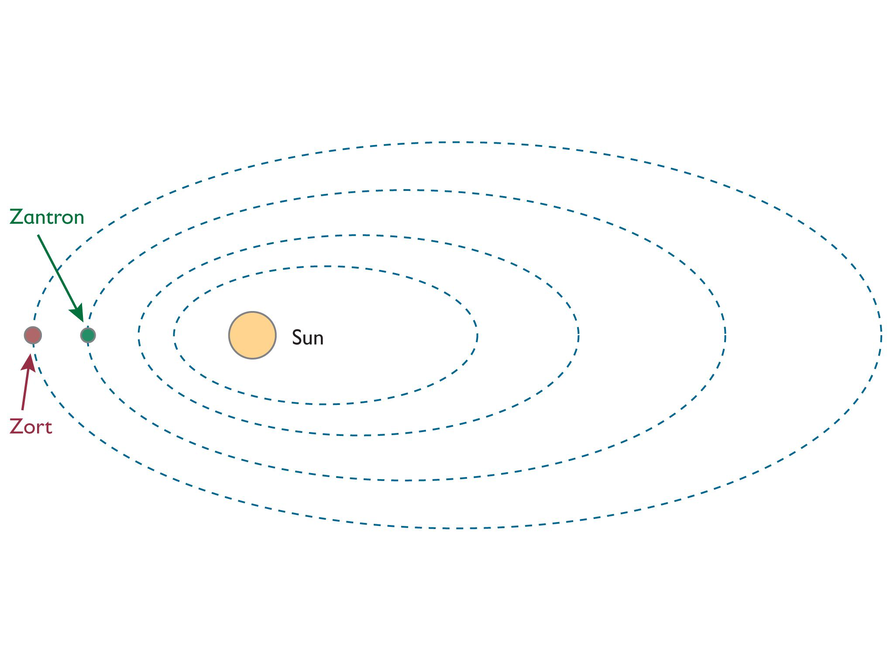
- Possible answer: The green dots on the timeline below mark when Zantron will be back in the same spot, and the red dots mark when Zort will be back in the same spot.
You can see that the two planets will be in the same spot again in 60 months.
- Possible answer: This is the same as finding the least common multiple. Multiples of 12 represent the months when Zantron will be in the same spot; multiples of 20 represent the months when Zort will be in the same spot. The least common multiple of 12 and 20 is 60.
Work Time
Fourth Rock
The planet Zantron is an imaginary planet that is a lot like Earth. It is the third planet from its sun. Its year—the time it takes the planet to go around the sun—is exactly 12 months.
Zort—the fourth planet in that solar system—takes exactly 20 months.
Scientists on Zantron want to communicate with the colony on Zort, but their radio only works when the planets are aligned so that they are at the closest distance possible from each other.
- If the two planets are at their closest point now, how many months will it be before they are at their closest point again?
- Explain the math you used to get your answer.
Factors of a Number
Answers
- The answer is (b). The claim is true only for some values of n
- Possible answer: The number 24 has factors 6 and 2, and 12 is also a factor of 24. The number 18 has the factors 6 and 2, but 12 is not a factor of 18.
Work Time
Factors of a Number
Read the following mathematical claim:
For any whole number n greater than 6, if 6 and 2 are both factors of n, then 12 is also a factor of n.
- Decide whether the claim:
a. Is true for every value of n.
b. Is true for only some values of n.
c. Is not true for any values of n.
2. Defend your decision mathematically.
Common Factors
Answers
Since 20 is a factor of both p and q, you can rewrite p and q as
p = 20x
q = 20y
where x and y share no common factors other than 1.
Thus, any factor of 20 must also be a factor of both p and q.
The factors of 20 are 1, 2, 4, 5, 10, and 20. So these are all the factors that are common to p and q.
Work Time
Common Factors
Suppose that the greatest common factor of two positive integers p and q is .
- List all the other factors that must be common to p and q. How do you know that these numbers must be common factors?
History of Variables
Answers
- Reports will vary.
Work Time
History of Variables
Research the use of variables in the history of mathematics throughout the world.
What country or countries were variables first used in?
- When were they used there?
- What were they used for?
- Create a timeline showing the use of variables in one of the countries you read about, or create a map showing the time each country you read about started using variables.
In what ways has the use of variables changed over time? In what ways has it stayed the same?
Create a Video
Answers
- Videos wll vary.
Work Time
Create a Video
Create a video about expressions.
- Think about the key concepts and terminology involved with expressions.
- Develop a story line that encompasses those concepts.
- Shoot and edit the video.