- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Baseball Cards per Page
How Much Change?
Writing, Representing & Evaluating Expressions

Overview
Students represent problem situations using expressions and then evaluate the expressions for the given values of the variables.
Key Concepts
An algebraic expression can be written to represent a problem situation.
To evaluate an algebraic expression, a specific value for each variable is substituted in the expression, and then all the calculations are completed using the order of operations to get a single value.
Goals and Learning Objectives
- Develop fluency in writing expressions to represent situations and in evaluating the expressions for given values.
How Much Change?
Lesson Guide
Start the lesson by projecting the problem situation from the How Much Change? interactive and giving students time to complete the table.
For the price of any book, you can find the change due by subtracting the price of the book from $10.00. This pattern can be represented by 10 − n. The expression 10 − n summarizes a calculation that can be done for any price n, and represents the change from buying a book of that price. You can use the same expression for different prices.
Opening
How Much Change?
Imagine that you have $10.00 to spend at the bookstore.
- Complete the table in the Hw Much Change? interactive. For each price listed, write an expression to represent the change you would receive if you paid with a 10 dollar bill. The price includes tax.
- The first two columns are done for you.
INTERACTIVE: How Much Change?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will represent problem situations using expressions and then evaluate the expressions for the given values of the variables.
Opening
Represent problem situations using expressions, and then evaluate the expressions.
Ages
Lesson Guide
This lesson gives students an opportunity to gain fluency in writing expressions for situations and in evaluating those expressions with specific values for their variables.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Watch for students who make sense of problem situations in order to represent them as expressions.
Mathematical Practice 6: Attend to precision.
Identify students who accurately evaluate algebraic expressions for a given value of the variable.
Mathematical Practice 7: Look for and make use of structure.
Identify students who look for structure in expressions by parsing them into a sequence of operations and by making use of the structure to interpret the expression’s meaning in terms of the quantities represented by the variables.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who find regularity in a repeated calculation and express it with a general formula.
Interventions
Student does not understand the expression.
- How do you know your expressions are correct?
- What is an expression that matches this situation? Explain how you know.
- What does the [quantity] represent in your expression?
- What does the variable represent in your expression?
- How does your expression compare to your partner’s expression?
- How are they the same?
- How are they different?
- Do both expressions have the same value? Why or why not?
Student has a solution.
- Explain your strategy for writing the expressions.
- How did you know what operation(s) to use in your expressions?
- What does the variable represent in your expression?
- What does this term represent in your expression?
- Explain the steps you used to evaluate your expression.
Answers
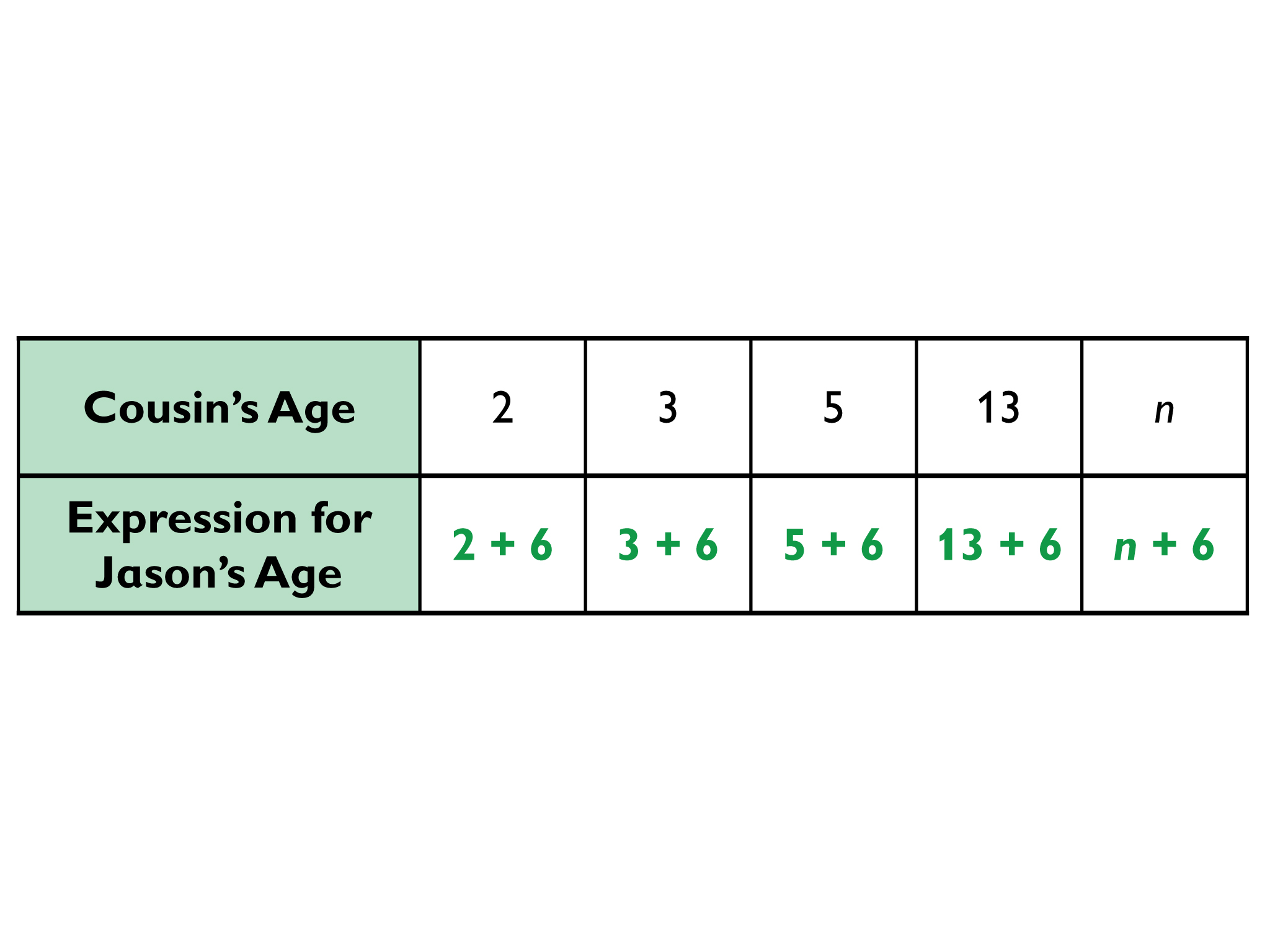
- Table:
- In this problem, n represents Jason’s cousin’s age.
Work Time
Ages
Jason is 6 years older than his cousin.
- Complete the table in the Ages interactive.
- Explain what n represents in this situation.
INTERACTIVE: Ages
Hint:
What operation can you use to show that Jason is 6 years older than his cousin?
Baseball Cards
Lesson Guide
This lesson gives students an opportunity to gain fluency in writing expressions for situations and in evaluating those expressions with specific values for their variables.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Watch for students who make sense of problem situations in order to represent them as expressions.
Mathematical Practice 6: Attend to precision.
Identify students who accurately evaluate algebraic expressions for a given value of the variable.
Mathematical Practice 7: Look for and make use of structure.
Identify students who look for structure in expressions by parsing them into a sequence of operations and by making use of the structure to interpret the expression’s meaning in terms of the quantities represented by the variables.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who find regularity in a repeated calculation and express it with a general formula.
Interventions
Student does not understand the expression.
- How do you know your expressions are correct?
- What is an expression that matches this situation? Explain how you know.
- What does the [quantity] represent in your expression?
- What does the variable represent in your expression?
- How does your expression compare to your partner’s expression?
- How are they the same?
- How are they different?
- Do both expressions have the same value? Why or why not?
Student has a solution.
- Explain your strategy for writing the expressions.
- How did you know what operation(s) to use in your expressions?
- What does the variable represent in your expression?
- What does this term represent in your expression?
- Explain the steps you used to evaluate your expression.
Answers
- Table:
- In this problem, n represents the number of pages in the scrapbook.
Work Time
Baseball Cards
Denzel puts 6 baseball cards on each page of a scrapbook.
- Complete the table.
- Explain what n represents in this situation.
INTERACTIVE: Baseball Cards per Page
Hint:
What operation can you use to calculate the total number of cards in a scrapbook with 3 pages?
Money
Lesson Guide
This lesson gives students an opportunity to gain fluency in writing expressions for situations and in evaluating those expressions with specific values for their variables.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Watch for students who make sense of problem situations in order to represent them as expressions.
Mathematical Practice 6: Attend to precision.
Identify students who accurately evaluate algebraic expressions for a given value of the variable.
Mathematical Practice 7: Look for and make use of structure.
Identify students who look for structure in expressions by parsing them into a sequence of operations and by making use of the structure to interpret the expression’s meaning in terms of the quantities represented by the variables.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who find regularity in a repeated calculation and express it with a general formula.
Interventions
Student does not understand the expression.
- How do you know your expression is correct?
- What is an expression that matches this situation? Explain how you know.
- What does the [quantity] represent in your expression?
- What does the variable represent in your expression?
- How does your expression compare to your partner’s expression?
- How are they the same?
- How are they different?
- Do both expressions have the same value? Why or why not?
Student has a solution.
- Explain your strategy for writing the expressions.
- How did you know what operation(s) to use in your expressions?
- What does the variable represent in your expression?
- What does this term represent in your expression?
- Explain the steps you used to evaluate your expression.
Possible Answers
- Chen has the following amount of money in his wallet: 0.25n + 0.10(n − 8) + 0.05(3n).
- 0.25n represents the value of the quarters. 0.10(n − 8) represents the value of the dimes. 0.05(3n) represents the value of the nickels.
- If n = 10, then 0.25n + 0.10(n − 8) + 0.05(3n) = 4.20. Chen has $4.20 in his wallet.
Work Time
Money
Chen checked his wallet to see how much money he had. He counted n quarters, 8 fewer dimes than quarters, and 3 times as many nickels as quarters.
- Write an expression that represents the amount of money Chen has.
- Explain what each term in the expression represents.
- Evaluate the expression for n = 10.
Hint:
- Write an expression that represents the number of dimes. If there are 8 fewer dimes than quarters, that means there are n-8 dimes.
- Write an expression that represents the number of nickels.
- Then, since you want to represent the total amount, add the expressions together.
Bike Ride
Lesson Guide
This lesson gives students an opportunity to gain fluency in writing expressions for situations and in evaluating those expressions with specific values for their variables.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Watch for students who make sense of problem situations in order to represent them as expressions.
Mathematical Practice 6: Attend to precision.
Identify students who accurately evaluate algebraic expressions for a given value of the variable.
Mathematical Practice 7: Look for and make use of structure.
Identify students who look for structure in expressions by parsing them into a sequence of operations and by making use of the structure to interpret the expression’s meaning in terms of the quantities represented by the variables.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who find regularity in a repeated calculation and express it with a general formula.
Interventions
Student does not understand the expression.
- How do you know your expressions are correct?
- What is an expression that matches this situation? Explain how you know.
- What does the [quantity] represent in your expression?
- What does the variable represent in your expression?
- How does your expression compare to your partner’s expression?
- How are they the same?
- How are they different?
- Do both expressions have the same value? Why or why not?
Student has a solution.
- Explain your strategy for writing the expressions.
- How did you know what operation(s) to use in your expressions?
- What does the variable represent in your expression?
- What does this term represent in your expression?
- Explain the steps you used to evaluate your expression.
Possible Answers
- Denzel rode the following distance on his bike today: 5t + 2s.
- 5t represents the distance he rode in 5 hours at t miles per hour. 2s represents the distance he rode in 2 hours at s miles per hour.
- If t = 15 and s = 20, then 5t + 2s = 115. Denzel rode his bike a total of 115 miles today.
Work Time
Bike Ride
Denzel wants to know how far he rode on his bike today. He biked for 5 hours at a speed of t miles per hour, and then for 2 hours at a speed of s miles per hour.
- Write an expression that represents how far he rode.
- Explain what each term in the expression represents.
- Evaluate the expression for t = 15 and s = 20.
Hint:
- Write an expression that represents how far Denzel rode for 5 hours at t miles per hour. Then write an expression that represents how far Denzel rode for 2 hours at s miles per hour. Finally, add the expressions to represent how far Denzel rode for the whole day.
Prepare a Presentation
Preparing for Ways of Thinking
As students work, look for:
- Evidence that students can comfortably write numerical expressions.
- Students who abstract from repeated calculations with numerical expressions to arrive at algebraic expressions.
- Students who understand what the variable(s) represent in each situation.
- Students who generate algebraic expressions to represent situations without first abstracting them from a pattern of numerical calculations.
Challenge Problem
Possible Answers
- Answers will vary.
Work Time
Prepare a Presentation
- Explain how you wrote your expressions.
- Define what each term in the expressions represent.
- Show how you evaluated the expressions for the given values.
Challenge Problem
- Write a problem similar to the one about Denzel or Chen and find the solution.
- Then exchange problems with a partner and solve each other’s problems.
Make Connections
Lesson Guide
Have individual students give their presentations. By the end of the discussion, students should understand each others' methods and make connections between the methods.
Select a variety of work with an eye to:
- Making sense of the situations.
- Connecting algebraic expressions to those situations.
- Understanding the meaning of each term and variable in the expressions.
Ask questions such as the following:
- How can you represent this situation using an expression?
- Explain what the different parts of your expression mean.
- Did anyone represent the problem a different way? Explain why you represented it this way.
- How can you evaluate your expression? Can you use these same steps to evaluate the expression for a different value of the variable?
- What does your answer mean?
Performance Task
Ways of Thinking: Make Connections
Takes notes about your classmates’ approaches to writing and evaluating expressions.
Hint:
As your classmates present, ask questions such as:
- How does your expression represent the situation?
- What are the known quantities?
- How did you know what operation to use?
- What does the variable represent?
- What does each term represent?
- What steps did you use to evaluate the expression?
- What does your answer mean?
Algebraic Expressions
Mathematics
Have pairs quietly discuss how to write algebraic expressions to represent problem situations and then how to evaluate those expressions by substituting values for the variables.
As student pairs discuss together, listen for students who may still have difficulty understanding how to write and evaluate algebraic expressions. Make note of any misconceptions you want to clarify during the class discussion. Then discuss the Summary as a class.
Formative Assessment
Summary of the Math: Algebraic Expressions
Read and Discuss
- A situation can be represented using an algebraic expression.
- You can evaluate the expression by substituting values for the variables in the expression and then performing the operations.
Hint:
Can you:
- Describe how to write algebraic expressions to represent problem situations?
- Describe how to evaluate algebraic expressions?
Correct Mistakes
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
SWD: Some students with disabilities may struggle to explain their mathematical reasoning in words. Provide sentence starters and/or paragraph frames to support students with this task. This will allow students to better explain their findings during discussion time.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
Interventions
Student has difficulty getting started.
- What do you need to do?
- How can you tell if the work is right or wrong?
- Can you find one problem that you know is done correctly?
- Can you find one problem that you know is done incorrectly?
Student does not understand when the distributive property is being used incorrectly.
- What does the distributive property say?
- Can you find one problem where the distributive property is being used correctly?
- Can you find one problem where the distributive property is being used incorrectly?
Student does not recognize when parentheses in an expression are being interpreted incorrectly.
- What do parentheses in an expression tell you?
- Can you find one problem where what is inside the parentheses is not interpreted correctly?
- Can you find one problem where what is inside the parentheses is interpreted correctly?
Student identifies incorrect work correctly, but does not adequately explain why the work is incorrect.
- Can you explain why the work you identified as wrong is wrong?
Student presents work poorly.
- Is your work shown clearly?
- Have you given enough explanation and is it clear?
Student identifies correct and incorrect work and gives good explanations of why a piece of work is wrong.
- Imagine you are a teacher again. Can you write a multiple-choice question where you are given an expression and the question is to identify the equivalent expression among four options? Trade with a friend and answer each other’s questions.
Answers
Problem 1
- Emma does not distribute the x over both the y and z. Chen answers correctly.
- Emma answers correctly. Chen incorrectly adds the unlike terms 4m and 8.
- Emma answers correctly. Chen incorrectly subtracts the unlike terms (5n)2 − n.
- Emma does not distribute the 7 correctly. She subtracts 3 from 32 instead. Chen answers correctly.
Problem 2
- Emma again does not distribute the number in front of the parentheses correctly. She does not multiply the second term in the parentheses.
- Chen incorrectly adds the terms 8x and 14 to get 22x, and subtracts 10 from 15x to get 5x. The correct answer is 23x + 4.
The most common type of error that Emma made was that she did not distribute a multiplier over a whole quantity in parentheses.
The most common type of error that Chen made was that he added terms that are not alike.
Formative Assessment
Correct Mistakes
Work on this Self Check by yourself.
Imagine that you are the teacher. Decide whether the work shown is correct or incorrect. If you see an incorrect answer, do the following:
- Cross it out and replace it with a correct answer.
- Explain what is wrong using words or diagrams.
What was the most common type of error that Emma made?
What was the most common type of error that Chen made?
Emma’s and Chen’s Work
Answers
Problem 3
- Emma does not distribute the multipliers n and 2 correctly. She does not multiply the second term. She also adds 3 + 2 + 14 incorrectly and gets 15 rather than 19.
- Chen again combines unlike terms. He factors out n from 2n2 to get 2. The correct answer should be 2n2 + 17n − 10.
Problem 4
- Emma does not distribute the multipliers 2 and 3 correctly. She does not multiply the second terms by 2 and by 3. She also mis-copies 5m as 15m.
- Chen again incorrectly combines unlike terms. He factors out m from 5m + 2n + 3m to get 10m. He also makes the same mistake as Emma (but only once) and forgets to multiply 3 and 2 in 3(m + 2). The correct answer should be 8m + 2n + 14.
2. The most common type of error that Emma made was that she did not distribute a multiplier over a whole quantity in parentheses.
3. The most common type of error that Chen made was that he added terms that are not alike.
Formative Assessment
Emma's and Chen's Work
Emma and Chen have done more work. With your partner, decide whether their work is correct or incorrect. If you see an incorrect answer, do the following:
- Cross it out and replace it with a correct answer.
- Explain what is wrong using words or diagrams.
What was the most common type of error that Emma made?
What was the most common type of error that Chen made?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students learned about using expressions.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
What I learned today about using expressions is …