- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Four Types Of Angles

Overview
Students learn about four types of angles: adjacent, vertical, supplementary, and complementary. They explore the relationships between these types of angles by folding paper, measuring angles with a protractor, and exploring interactive sketches.
Key Concepts
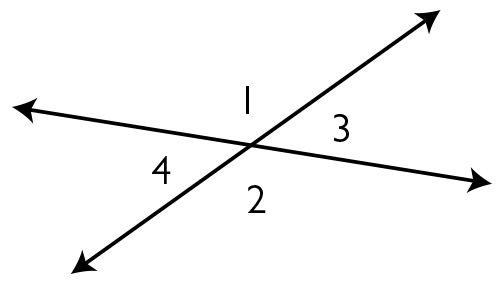
- Adjacent angles are two angles that share a common vertex and a common side, but do not overlap. Angles 1 and 2 are adjacent angles.
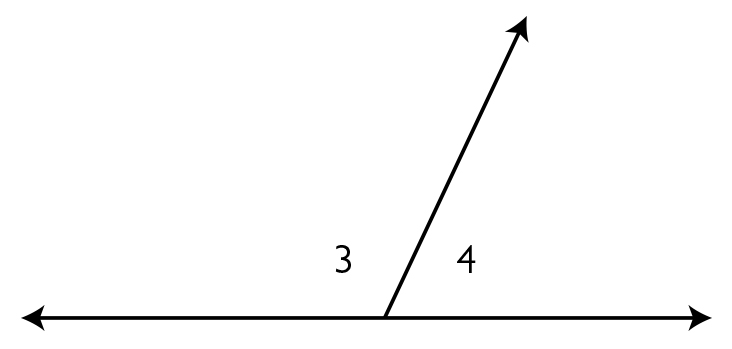
- Supplementary angles are two angles whose measures have a sum of 180°. Angles 3 and 4 are supplementary angles.
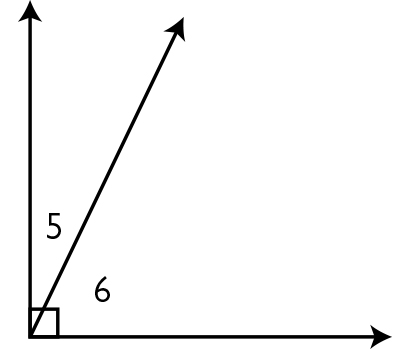
- Complementary angles are two angles whose measures have a sum of 90°. Angles 5 and 6 are complementary angles.
- Vertical angles are the opposite angles formed by the intersection of two lines. Vertical angles are congruent. Angles 1 and 2 are vertical angles. Angles 3 and 4 are also vertical angles.
Goals and Learning Objectives
- Measure angles with a protractor and estimate angle measures as greater than or less than 90°.
- Understand the definition of vertical, adjacent, supplementary, and complementary angles.
- Explore the relationships between these types of angles.
Think About Angles
Lesson Guide
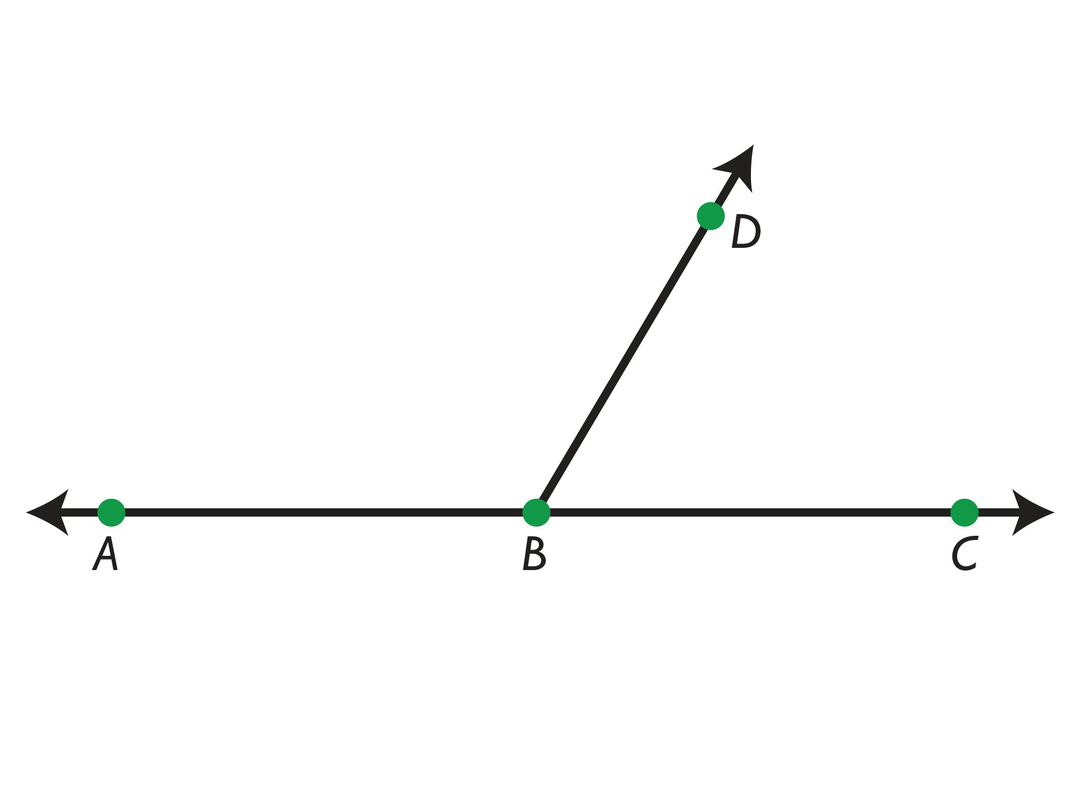
After students see the opening figure, ask them how they could describe the figure.
SWD: Though informal, discuss as an introduction/preview for students with disabilities. Emphasize they will be introduced to angle relationships. This will support students as they work to determine salient information throughout the lesson.
Mathematics
Students may see the following and should include in their discussion their explanations of how they came to those conclusions:
- An acute angle and an obtuse angle
- Two angles that share a common side
- Two angles that are supplementary
- A straight angle
- Estimated angle measures—perhaps 60° and 120°
ELL: Thinking aloud is one strategy for making learning visible. When teachers think aloud, they are externalizing their internal thought processes. Doing so may provide students with insights into your mathematical thinking and ways of estimating angle measures. It also helps to model accurate mathematical language.
Opening
Think About Angles
- Describe the angle(s) in this figure.
- Discuss your ideas with your class.
Types of Angles
Teacher Demo
Measure the angle(s) to demonstrate and review how to use a protractor. Discuss the size of each angle relative to 90° and the fact that the angles add up to 180°. When measuring the angles, review how angles are named.
SWD: As you model how to measure angles given using a protractor, make sure that you are annotating the steps you use to measure angles.
Opening
Types of Angles
Discuss the following with your classmates.
- ∠ABD and ∠CBD are adjacent angles. Adjacent angles share a vertex and a side.
- ∠ABD and ∠CBD are also supplementary angles. The measures of supplementary angles add up to 180°.
- ∠ABC is a straight angle.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore the relationships between adjacent, supplementary, complementary, and vertical angles.
Opening
Explore the relationships between adjacent, supplementary, complementary, and vertical angles.
Measure Angles
Lesson Guide
Hand out protractors and 8½ in. x 11 in. sheets of paper. For the paper folding activity, have students work individually, but have them collaborate with a partner and share their results with their group or table.
ELL: Make sure you demonstrate and verbally explain the activity step by step to ensure that ELLs understand what they are being asked to do. Students may still need support with the folding activity and measuring angles with a protractor. If students are still struggling, pull a small group for direct instruction.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Look for students who use the protractor correctly to accurately measure the angles.
Interventions
Student does not use the protractor correctly.
- Is the 0° line along one of the sides of the angle?
- Is the vertex at the center of the protractor?
Student does not read the protractor and/or interpret the angle correctly.
- Is the angle measure greater than or less than 90°?
- Is the angle opening to the left or right?
Possible Answers
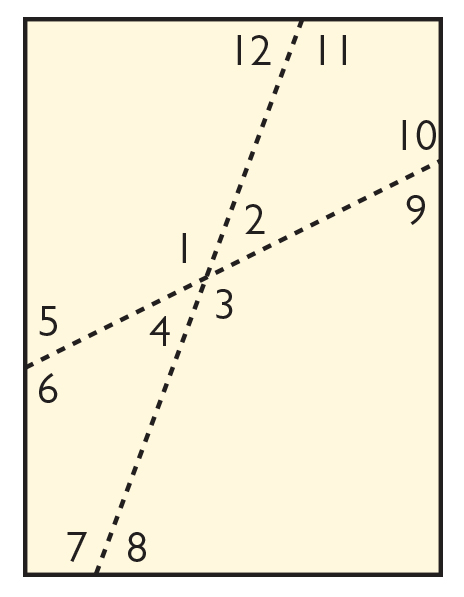
- The rectangle shown is an example of what the folded sheet of paper might look like. It is labeled to make it easier to refer to specific angles.
- Angles 1 and 2, angles 2 and 3, angles 3 and 4, and angles 4 and 1 are all supplementary. They should also see that angles 1 and 3, and angles 2 and 4 are congruent. (These are vertical angles.) Students may also notice that the four angle measures add up to 360°. (There are 360° in a circle.)
- Angles 5 and 6, angles 7 and 8, angles 9 and 10, and angles 11 and 12 are all supplementary. They should also see that angles 5 and 9, angles 6 and 10, angles 7 and 11, and angles 8 and 12 are congruent (a preview of angles formed by a transversal). This leads to several pairs of supplementary angles that are not adjacent: angles 5 and 10, angles 6 and 9, angles 7 and 12, and angles 8 and 11 (again, a preview of angles formed by a transversal).
Work Time
Measure Angles
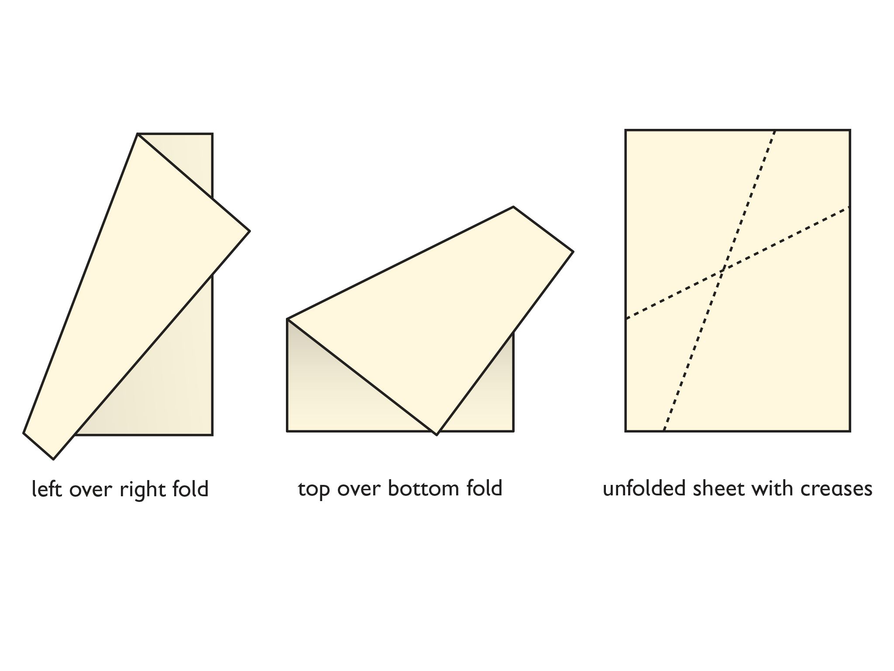
- Start with a sheet of paper. Fold the left edge over the right edge at a slant. Unfold. Fold the top edge over the bottom edge at a slant. Unfold.
- Using your protractor, measure each of the four angles created by the intersection of the folds. Write the angle measures on the paper. What do you notice?
- Measure each of the angles formed by the folds and the edges of the paper. What do you notice?
Explore Angles
Lesson Guide
For the Angles Sketch interactive, have students work individually or with a partner.
Mathematical Practices
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Most students will be able to generalize about supplementary angles and vertical angles, particularly after using the sketches and seeing repeated cases.
Interventions
Student does not see that the adjacent angles are supplementary.
- At the measure of each angle shown on the protractor, what do you notice about the sum of the two angles shown?
[common error] Student thinks that the length of the ray affects the size of the angle.
- If the sides of the angle were longer or shorter, would the measure of the angle change?
Possible Answers
- In the first sketch the angles are always supplementary. As one angle increases in size, the other decreases. In the second sketch, students should notice the sum of the supplementary angles and the congruent vertical angles. In the third sketch, students should notice that the angle sum is always 90° and that the angles are complementary.
- If angles 1 and 2 are congruent, they both have a measure of 90°.
- If angles 3, 4, 5, and 6 are congruent, they all have a measure of 90°. They are all right angles.
Work Time
Explore Angles
Use the Angles Sketch interactive to explore each set of angles:
- The line and ray forming a straight angle
- The intersecting lines
- The rays forming a right angle
Answer the following questions.
- Write at least one observation about each set of angles 1–8.
- Can you make angles 1 and 2 congruent? If so, what type of angle did they become?
- Can you make angles 3, 4, 5, and 6 congruent? If so, what type of angle did they become?
INTERACTIVE: Angles Sketch
Hint:
Try adding different angles together. What is their sum? Which angles are congruent?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion.
Look for students who:
- Identified the vertical angles as congruent.
- Observed that the angles on opposite sides of the sheet of paper were congruent.
- Observed pairs of supplementary angles in the sheet of paper that were not adjacent.
Challenge Problem
Answers
- Since one angle is five times larger than the other, it is of 90°, while the other angle is of 90°.
× 90° = 75°
× 90° = 15°
Check: 15° ⋅ 6 = 90°
Students could also solve algebraically:
5x + x = 90°
6x = 90°
x = 15°
Work Time
Prepare a Presentation
Summarize the observations you made about angle relationships and the sums of angles.
Challenge Problem
- Two complementary angles like ∠7 and ∠8 form a 90° angle. Can you make one angle 5 times the measure of the other angle?
Make Connections
Ways of Thinking
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson. Ask questions such as the following:
- On your sheet of paper, which angles are supplementary?
- Are all of these pairs of angles adjacent?
- Which angles are congruent?
- Which angles are complementary?
- Which angles are adjacent?
- What is the sum of the four angle measures in the middle of the paper? Why?
- Which angles are congruent? Why do you think they are congruent?
- Why are vertical angles congruent? (Answer: If angle 1 and angle 2 are supplementary and angle 2 and 3 are supplementary, then angle 1 and angle 3 must be congruent.)
- What conclusions can you draw from exploring the first two sketches?
- What conclusion can you draw from the third sketch? How can you describe the angles in this sketch? (Answer: adjacent and complementary)
- You were able to make all of the angles congruent in the sketches. Would this be possible in folding the sheet of paper? (Answer: Yes, if the paper were folded vertically and horizontally in half. Remind students that a 90° angle is called a right angle.)
- How did [students] organize their thoughts differently? Which makes more sense to you? Which brought out the structure of the mathematics?
- How did [students] make sense of the problem?
- Could you state what [students] said in a different way?
ELL: Encourage students to use diagrams, if necessary, to explain their congruent angle and supplementary angle relationships. Have students mark the angle relationships they will be discussing during this “Ways of Thinking” section.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ observations concerning angle relationships and the sum of angles.
Hint:
As your classmates present, ask questions such as:
- Which angles were congruent? Why do you think they were congruent?
- What was the sum of the angles?
Types of Angles
Lesson Guide
Have students work in pairs to read and discuss the information about supplementary angles, adjacent angles, vertical angles, and complementary angles. Make sure that students discuss each type of angle. It might be helpful for students to draw a picture of each type of angle after they have discussed the summary.
Formative Assessment
Summary of the Math: Types of Angles
Read and Discuss
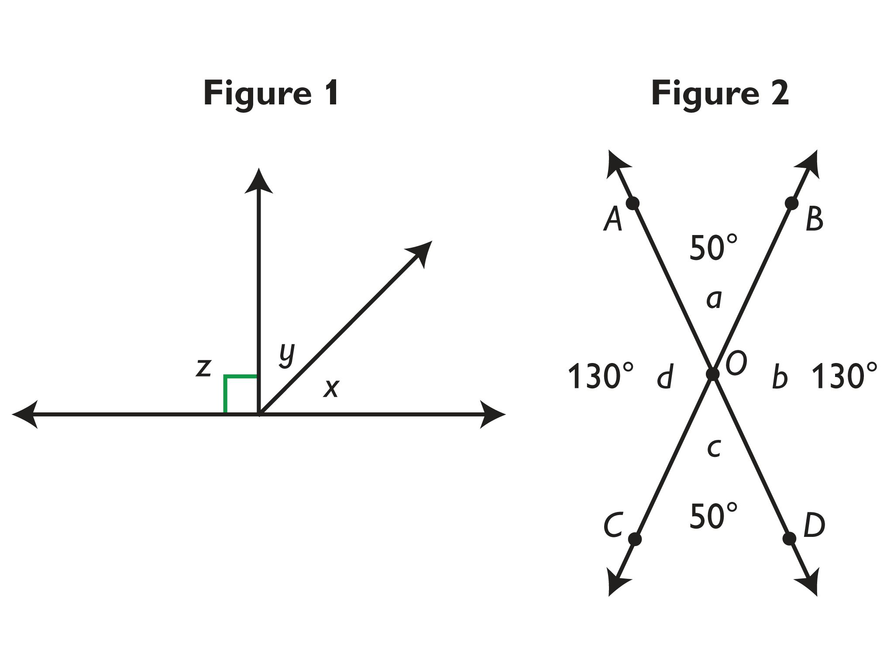
- Supplementary angles are two angles with measures that add up to 180°. Two supplementary angles together form a straight angle.
- In Figure 2, ∠c and ∠d are supplementary angles.
- Complementary angles are angles with measures that add up to 90°. Two complementary angles together form a right angle.
- In Figure 1, ∠x and ∠y are complementary angles.
- Two intersecting lines create four angles. Each pair of equal angles are vertically opposite angles or vertical angles.
- In Figure 2, ∠a and ∠c are vertical angles.
- Adjacent angles are angles that are next to each other; they share a vertex and a side.
- In Figure 2, ∠a and ∠d are adjacent angles.
Hint:
Can you:
- Explain when adjacent angles are supplementary?
- Explain what is true of vertical angles?
- Describe the angle formed by two angles that are complementary and adjacent?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what similarities and differences students notice about complementary and supplementary angles.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think complementary and supplementary angles are similar in these ways… and different in these ways …