- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Mathematical Practice 5
Triangles Sketch
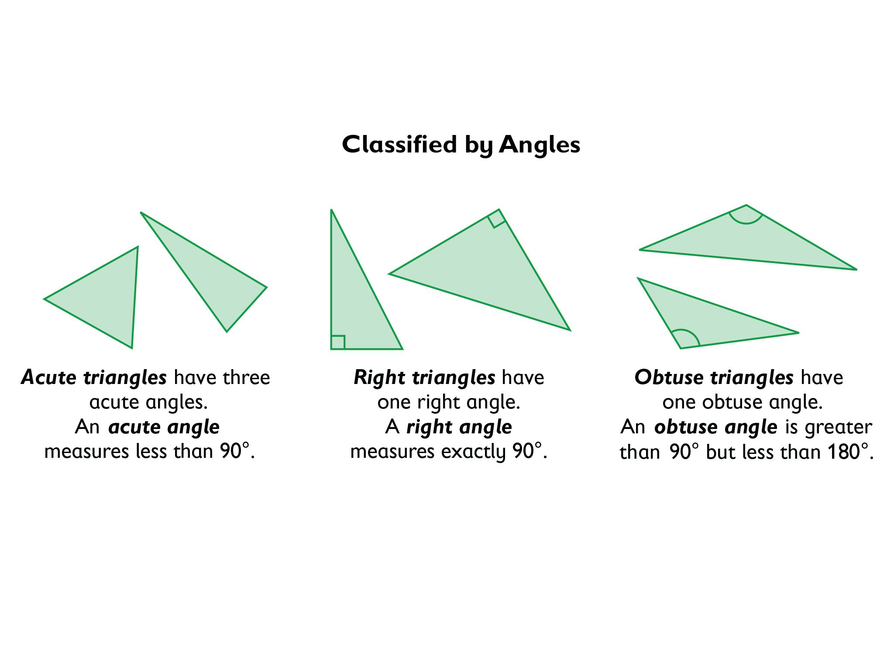
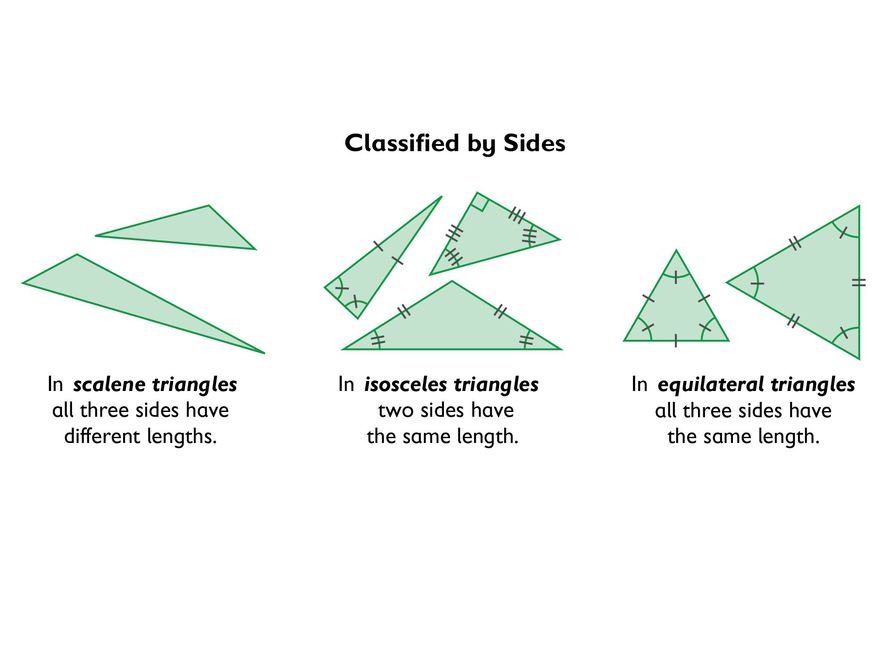
Classifying Triangles

Overview
Students learn to classify triangles by the size of the angles and the measures of the sides.
Key Concepts
- Triangles are polygons with three sides.
- Scalene triangles have all sides with a different length and all angles with a different measure.
- Isosceles triangles have two sides with the same length and two angles with the same measure.
- Equilateral triangles have all sides with the same length and all angles with the same measure.
- Acute triangles have all angles with a measure less than 90°.
- Obtuse triangles have one angle with a measure greater than 90°.
- Right triangles have one angle with a measure of 90°.
ELL: Keep in mind that consistency at the beginning is very important as students begin to learn and apply math vocabulary.
Goals and Learning Objectives
- Explore conditions that result in triangles.
- Identify types of triangles based on the measure of the angles or the measures of the sides.
Types of Triangles
Lesson Guide
Have students view the triangles.
SWD: Learning new domain-specific vocabulary can be a challenge for students with disabilities. Preview and/or pre-teach the new vocabulary terms in this lesson. When possible, promote connections to students' background knowledge and to previous lessons in this unit.
- Scalene triangle
- Isosceles triangle
- Equilateral triangle
- Acute triangle
- Obtuse triangle
- Right triangle
ELL: When discussing triangles, make a point of writing the students' responses on the board. This will assist ELLs by giving them written and oral access to the class' observations. Have students write all important information in their notebook.
Mathematics
Discuss the different ways triangles can be classified. Have students identify different types of triangles in the classroom.
Opening
Types of Triangles
Discuss the following with your classmates.
- Triangles can be classified by the size of their angles.
- Triangles can also be classified according to the lengths of their sides.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore the properties of triangles.
Opening
Explore the properties of triangles.
Classify Triangles
Lesson Guide
For the Triangles Sketch interactive, students may work individually or with a partner. Make sure that students understand how to manipulate the figures.
SWD: Make sure all students understand the task at hand. Have students retell the task back to you in their own words so you can assess their understanding.
ELL: Allow ELLs to write up parts of their answers. It can be hard for ELLs to explain the whole phrase, but they can either draw what they mean or use their diagram from the interactive. This will help them prepare for the Ways of Thinking sections of the lesson. Allow students to annotate notes next to their drawings.
Interventions
Student has difficulty getting started.
- What do you know about each type of triangle?
- How many sides are congruent?
- How does an acute or obtuse angle compare to a right angle?
[common error] Student thinks that a triangle is defined by angles or sides, but not both.
- How many sides are congruent in a scalene triangle? Isosceles triangle? Equilateral triangle?
- How many angles are congruent in a scalene triangle? Isosceles triangle? Equilateral triangle?
Possible Answers
- Equilateral triangles have angles with the same measure. Isosceles triangles have two angles with the same measure. Scalene triangles have all angles with different measures.
- A right triangle can be scalene or isosceles; an acute triangle can be scalene, isosceles, or equilateral; and an obtuse triangle can be scalene or isosceles.
- Students should see that the angle sum of an exterior angle and its adjacent interior angle is always 180°. As they manipulate the triangle, they should see that as one angle gets larger (perhaps obtuse), the other angles get smaller, and vice versa.
Work Time
Classify Triangles
Use the Triangles Sketch interactive to explore equilateral, isosceles, scalene, acute, obtuse, and right triangles.
- For each triangle that is classified by sides, state everything you notice about the angles.
- For each triangle that is classified by angles, state everything you notice about the sides.
- Use the Exterior Angles button. What do you notice about the relationship of the exterior angles to the interior angles for each type of triangle?
INTERACTIVE: Triangles Sketch
Hint:
- How are the angles in each figure related? What do the angles tell you about the figure?
- For each triangle classified by sides, what do you notice about the angles?
- Do any of the triangles that are classified by angles also have one of the characteristics of triangles that are classified by sides?
- What is the sum of the interior angles for each triangle?
- How does the sum of two of the angles compare to the measure of the third angle?
- If one of the angles is a right angle, what is the sum of the other two angles?
Explore Triangles
Interventions
Student does not see that certain sides will form a triangle.
- Have you tried making the bottom side shorter?
- Why won't the two sides meet?
Student has a solution.
- Why is the third angle a right angle?
- Can you always form a triangle if one angle is obtuse?
Possible Answers
- It is not possible to construct a triangle where the sum of the other two sides is less than or equal to the base length.
- If one of the sides is longer than the base length, it is always possible to construct a triangle by changing the length of the third side to an appropriate length.
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
- The interior angles of a triangle always add up to 180°. Because of this, only one of the angles can be 90° or more.
Work Time
Explore Triangles
Use the Making Triangles interactive to explore how the lengths of the sides determine whether you can construct a triangle.
- Start with a base length of any size. Make the sum of the length of the other two sides less than the base length. Can you make a triangle? Explain why.
- Start with a base length of any size. Make one of the sides longer than the base. Can you make a triangle? Explain why.
Using the explorations you just did, generalize:
- If you were given the length of 3 sides, how could you determine if those 3 lengths would make a triangle?
- If you were given 3 angles, how could you determine if those 3 angles would make a triangle?
INTERACTIVE: Making Triangles
Hint:
- If you add the lengths of two of the sides, what do you know about the relationship between this sum and the length of the third side?
- Can you move a side to the other side and make another triangle?
- If you choose two angles, what conditions will allow you to make a triangle?
- What conditions will not allow you to make a triangle?
- If the one side does not change, what side lengths will not make a triangle?
Prepare a Presentation
Preparing for Ways of Thinking
Look for the following students to share during the Ways of Thinking discussion.
- Students who understand how the measures of the angles in a triangle are related to each other
- Students who can do the Challenge Problem and explain why the angle measures in a triangle add up to 180°
- Students who understand the sketch about the lengths of the sides of a triangle and explain their conclusion
- Students who know that a right triangle has two complementary angles, but also see the reverse statement: if a triangle has complementary angles, it is a right triangle
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students may make conjectures and generalize about properties of triangles based on the many cases they have seen.
Mathematical Practice 6: Attend to precision.
Look for students who use multiple examples from the Triangle Sketch interactive to see that the angle sum in triangles always totals exactly 180°, and who understand that it is because of the increased accuracy of the sketches. Also, because of the accuracy of the measurements, students will see that it is difficult to be precise—for example, in getting all three angles to be exactly 60° or all three sides to have the same length.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Students have the appropriate tools to use strategically in the sketches, but proficient students will approach the sketches systematically, rather than randomly trying things. These students will be looking for and testing conjectures. Notice students who can make conjectures about triangles, seeing the common characteristics.
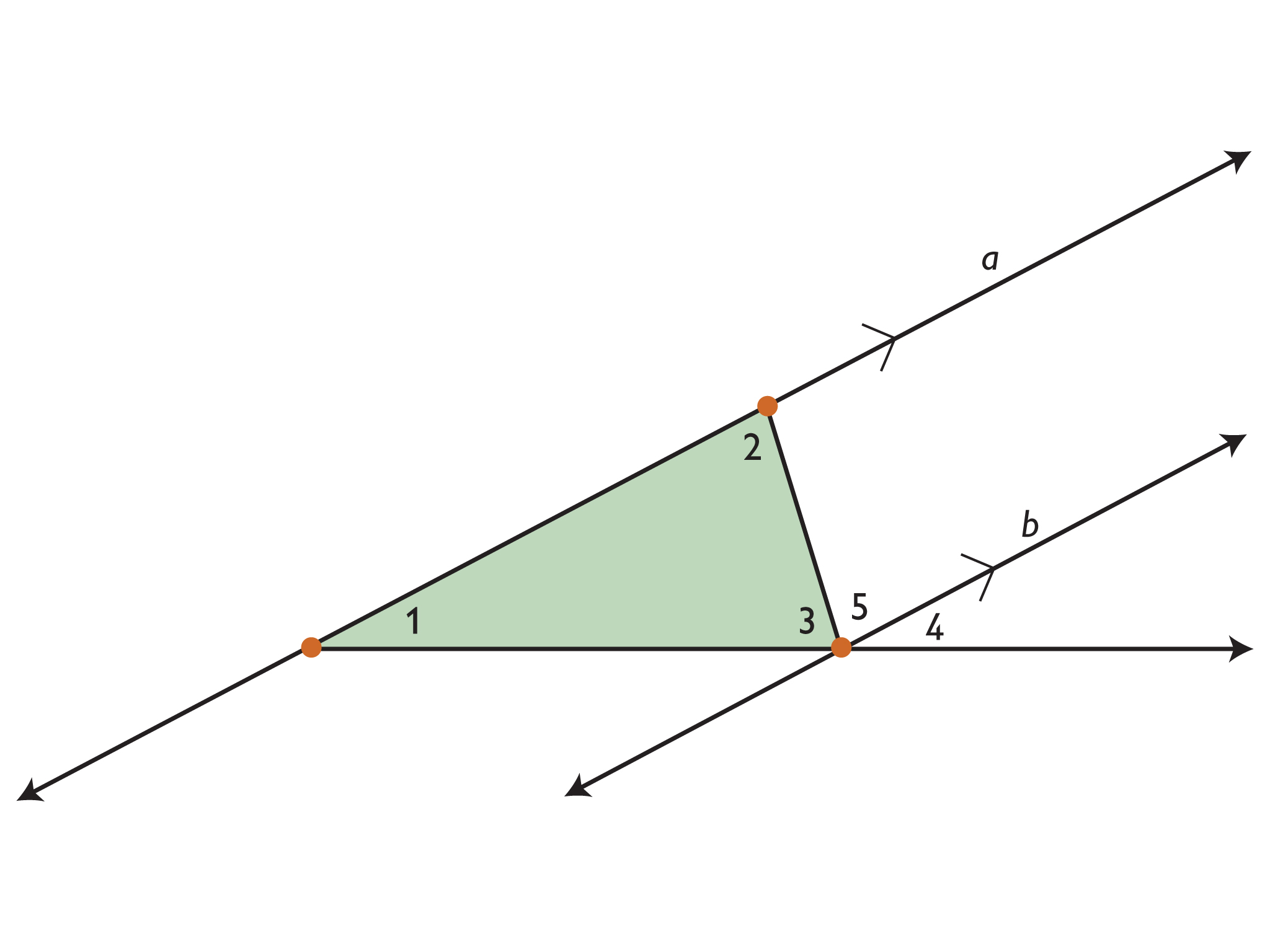
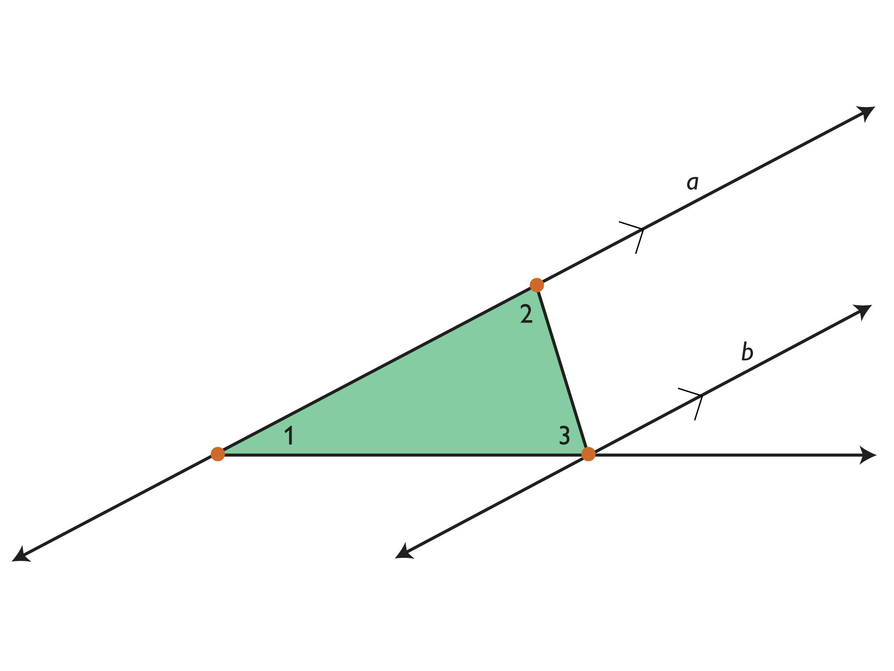
Challenge Problem
Answer
- Diagram:
Since line a and line b are parallel, ∠1 ≅ ∠4 and ∠2 ≅ ∠5. The sum of the measures of angles 1 and 2 is the sum of the measures of angles 4 and 5 (the supplementary angle to angle 3): m∠1 + m∠2 = m∠4 + m∠5. The measures of angles 3, 4, and 5 add up to 180° because they form a straight angle, so the measures of angles 1, 2, and 3 also add up to 180°.
Work Time
Prepare a Presentation
List your conclusions about the properties of triangles. Provide examples to illustrate your conclusions.
Challenge Problem
- Why do the angles in a triangle add up to 180°?
This figure may help you explain your thinking. Note that lines a and b are parallel.
Make Connections
Lesson Guide
Have students share the different things they did with each sketch or anything they thought was unusual for each sketch.
Mathematics
Lead a discussion, having students share their thinking. Ask questions such as the following:
- When you added the angle measures, did they come out to exactly 180°? Why?
- How do you think angle measures and side lengths are related in triangles?
- What is true for all triangles?
- If a triangle has complementary angles, what kind of triangle is it?
- How could you determine if a triangle could be drawn given the lengths of three sides?
- How could you determine if a triangle could be drawn given the measures of three angles?
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ conclusions regarding the angles and sides of a triangle.
Hint:
As your classmates present, ask questions such as:
- When you added the angle measures, was the sum exactly 180°? Explain.
- How do you think angle measures and side lengths are related in triangles?
- What is true for all triangles?
- If a triangle has complementary angles, what kind of triangle is it?
- Could a side of a triangle be parallel to another side?
- If you know the lengths of two sides, what can you tell about the length of the third side?
Use Appropriate Tools
Mathematical Practices in Action
Mathematical Practice 5: Use appropriate tools strategically.
Have students watch the video and listen to the dialogue between Karen and Maya. This video shows students engaged in Mathematical Practice 5: Use appropriate tools strategically. What did Karen and Maya discover? Have student evaluate Karen's summary of which tools she would use when.
This video shows students that different tools work better to solve different problems. Even though the problems look similar, sometimes the tools used to solve them most efficiently can be different.
Have students brainstorm the kinds of tools that they use in mathematics. Their list might include such things as graphs and rulers. Even pencil and paper is a tool!
Performance Task
Ways of Thinking: Use Appropriate Tools
Watch the video to see Karen and Maya discussing the different tools they use to construct triangles.
- What did Karen and Maya find out about different tools?
- What tools were most appropriate for what problems?
- How would you know which tools you might select to help you solve the problems?
VIDEO: Mathematical Practice 5
Triangles
A Possible Summary
Equilateral triangles have angles with the same measure and all three sides the same length. Isosceles triangles have two angles with the same measure and two sides the same length. Scalene triangles have all angles with different measures and all three sides are different lengths. A right triangle has a 90° angle and can be scalene or isosceles. An acute triangle has all acute angles (less than 90°) and can be scalene, isosceles, or equilateral. An obtuse triangle has one obtuse angle (greater than 90°) and can be scalene or isosceles. The angle measures of a triangles have a sum of 180°. It is not possible to construct a triangle where the sum of the other two sides is less than or equal to the base length. If one of the sides is longer than the base length, it is always possible to construct a triangle by changing the length of the third side to an appropriate length.
Formative Assessment
Summary of the Math: Triangles
Write a summary about the angles and sides in triangles.
Hint:
Check your summary:
- Do you explain the relationship of the angles in a triangle?
- Do you explain what conditions (number of sides, angles measures, and so on) will/won’t allow you to make a triangle?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to determine if students have additional questions about the properties of the angles and sides of triangles.
SWD: Some students may struggle with the task of writing a summary of the mathematics from the lesson. Possible supports:
- Prior to writing the summary, have students discuss their ideas with a partner or adult and rehearse what they might write.
- Allow students to map out their ideas in outline form or in a concept web
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about triangles is…