Characteristics Of Parallelograms

Overview
Students learn more about the characteristics of parallelograms by folding paper and measuring the angles in a parallelogram. Students use a ruler and protractor to draw parallelograms with given properties. Then, students use a ruler and protractor to draw a rectangle.
Key Concepts
- Opposite angles of a parallelogram are congruent.
- Consecutive angles of a parallelogram are supplementary.
- Diagonals of a parallelogram bisect each other.
- Diagonals of a rectangle are congruent.
Goals and Learning Objectives
- Access prior knowledge of parallelograms.
- Understand that the sum of angle measures in any quadrilateral is 360°.
- Understand the relationship of the angles and diagonals in a parallelogram.
- Understand the relationship of the angles and diagonals in a rectangle.
Think About Parallelograms
Lesson Guide
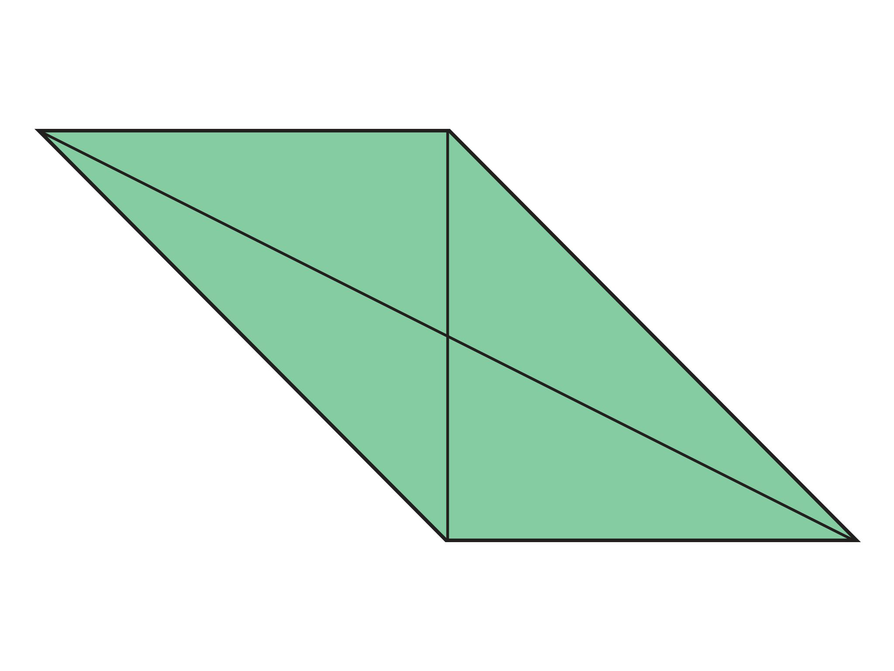
Have students view the opening figure and discuss the questions, “What makes this a parallelogram?” and “What do you notice about the parallelogram?”
ELL: Show any congruent sides and angles of a figure by coloring the corresponding congruent sides the same color and use “tick marks” so that students can clearly identify the congruent sides. Mark parallel lines with “arrows” to denote the lines that are parallel to each other.
Mathematics
Students should notice the following about the figure:
- The figure is a parallelogram because opposite sides are congruent and parallel.
- Also, the opposite angles appear to be congruent and the diagonals appear to be divided into two congruent segments.
Opening
Think About Parallelograms
On the first day of this unit, you folded paper to make this parallelogram.
Discuss the following with your classmates.
- What makes this figure a parallelogram?
- What do you notice about the parallelogram?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore angle relationships and diagonal relationships in parallelograms.
Opening
Explore angle relationships and diagonal relationships in parallelograms.
Make Quadrilaterals
Lesson Guide
Hand out protractors and 8½ in. x 11 in. sheets of paper to students. Have students work with a partner and share their results with their group or table.
SWD: Students with disabilities may need review and reinforcement of the major skills and concepts covered in this lesson. Have students use this time as an opportunity to review and reinforce how to accurately measure an angle with a protractor.
ELL: Modeling how to fold is essential for ELLs. It helps them clarify difficult concepts and/or directions. It also gives students the opportunity to ask questions, and it gives the instructor the opportunity to model effective learning strategies.
Possible Answers
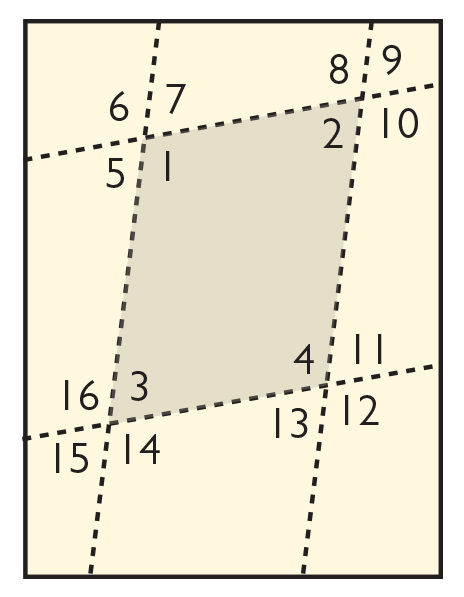
The rectangle shown is an example of what the folded sheet of paper might look like. It is labeled to make it easier to refer to specific angles.
- The figure is a parallelogram. The opposite sides appear to be parallel and look like they have the same length. The opposite sides of the paper are parallel, and when folded together, create parallel folds. These parallel folds form the figure.
- The measures of the angles vary. Students should notice that opposite angles are congruent (angles 1 and 4, and angles 2 and 3) and that adjacent angles are supplementary (angles 1 and 2, angles 2 and 4, angles 3 and 4, and angles 1 and 3).
- Students should see, for example, that angles 1 and 6 and angles 5 and 7 are vertical angles and are therefore congruent. They should see that angles 6 and 7, angles 1 and 7, angles 1 and 5, and angles 5 and 6 are supplementary. Because there are two pairs of supplementary angles at each intersection of the parallelogram, the sum of the four angles will be 360°. In other words, the sum of the three angles not contained in the parallelogram at each intersection will be equal to 360° minus the measure of the angle contained within the parallelogram. With this knowledge they can easily find the angle measures.
- Students should see that angles 1 and 10 and angles 2 and 5 are congruent. This explains why the consecutive angles are supplementary: angles 1 and 5 are supplementary and angle 5 is congruent to angle 2, so angles 1 and 2 are supplementary. Students may also notice that angles 6 and 12 and angles 9 and 15 are congruent. The congruent angles demonstrate the properties for parallelograms and the relationship between the interior angles and the exterior angles. Angles are supplementary or congruent as a result of the parallelogram being formed by pairs of parallel lines.
Work Time
Make Quadrilaterals
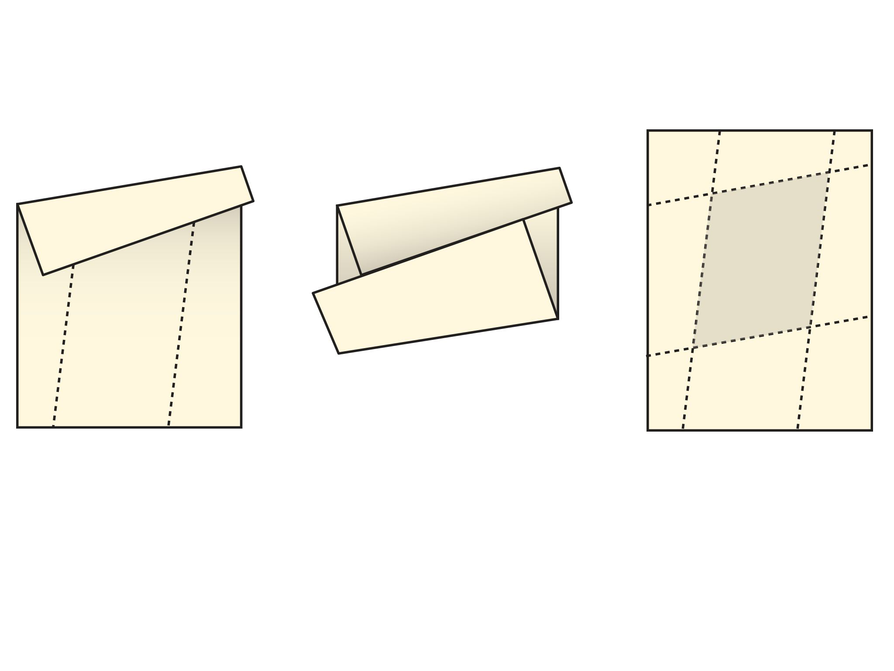
Start with a sheet of paper. Fold the left edge toward the center at a slant. Then fold the right edge toward the center so that the right edge meets the left edge. Unfold.
Repeat the steps above using the top and bottom edges.
Look at the shaded center figure that is outlined by the folds.
- What type of figure is this? How do you know? Why do you think this type of figure was formed as a result of folding the paper the way you did?
- Measure each of the four angles inside the figure and write the measurements on the paper. What do you notice?
- For each of the four angles you measured, there are three angles that share the same vertex but lie outside the figure. What is the sum of these three angles? How do you know?
- What congruent angles do you see? What do these angles tell you about the figure?
Draw a Quadrilateral
Lesson Guide
Have students continue to work with a partner and share their results with their group or table.
Interventions
Student does not correctly follow the directions to draw the parallelogram.
- What is the sum of supplementary angles?
- What is the measure of each angle you are drawing?
- Since the first angle is acute, what type of angle will the second angle be?
Possible Answers
- The side length is 4 in.
- The figure is a parallelogram because the opposite sides have the same length. Also, consecutive angles are supplementary and opposite angles are congruent.
- The two segments of each diagonal have the same length.
Work Time
Draw a Quadrilateral
On a new sheet of paper, draw a quadrilateral by following these steps:
- Draw a horizontal line that is 4 in. long.
- On the left side of the segment, construct an acute angle that opens to the right by drawing a line segment that intersects the left end of the horizontal line. Make the line 3 in. long.
- On the right side of the horizontal segment, construct an angle that is the supplementary angle to the first angle and that opens to the left by drawing a line segment that intersects the right end of the horizontal line. Make the line 3 in. long.
- Draw a line to connect the ends of the two 3-\ in. lines.
Use your finished quadrilateral to do the following.
- Measure the length of the last side that you drew. How long is it?
- Measure each of the angles. What type of figure did you draw? How do you know?
- Draw the two diagonals (the segments from one vertex to the opposite vertex). The diagonals will intersect, and the intersection will “divide” each diagonal into two segments. Measure the length of the two segments in each diagonal. What do you notice?
Hint:
- How are the angles in this figure related?
- What is the sum of the angles?
Draw a Rectangle
Lesson Guide
Have students continue to work with a partner and share their results with their group or table.
Interventions
Student is not sure how to draw the rectangle.
- What do you know about rectangles?
- What is the measure of an angle in a rectangle?
[common error] Student does not see the rectangle as a parallelogram because the sides are not slanted.
- What are the characteristics of a parallelogram?
- What are the characteristics of a rectangle?
- How are they the same? How are they different?
Possible Answers
- Most students choose two side lengths and draw a right angle using the protractor. The third side will be at a right angle, and the fourth side will connect the ends of opposite sides.
- Students should see that the segments of each diagonal have the same length. They should then see that all four segments of the diagonals have the same length, leading to the conclusion that the diagonals of a rectangle have the same length.
Work Time
Draw a Rectangle
On a new sheet of paper, using a protractor and its ruler side, draw a rectangle.
- What steps did you follow to draw the rectangle? How do you know that your figure is a rectangle?
- Draw the two diagonals (the segments from one vertex to the opposite vertex). Measure the length of the two segments in each diagonal. What do you notice?
Hint:
- How are the angles in the rectangle related?
- What is the sum of the angles in the rectangle?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion.
Look for students who
- Folded the sheet parallel to the sides, creating a rectangle.
- Identify the various pairs of congruent angles around the parallelogram.
- Notice that adjacent angles are supplementary.
- See that there are an infinite number of parallelograms with side lengths of 3″ and 4″.
- Understand that the diagonals bisect each other in a parallelogram.
- Understand that a rectangle is a parallelogram, so the diagonals bisect each other and the diagonals are the same length.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Look for students who can make conjectures and generalize about properties of parallelograms based on the many cases they've seen.
Mathematical Practice 6: Attend to precision.
- Look for students who see the importance of measuring angles and lengths accurately. Students who do not attend to precision may not draw the proper conclusions; for example, if the paper is not folded carefully and correctly, the diagonals will not be bisected, and students will not be able to make that conclusion.
Mathematical Practice 5: Use appropriate tools strategically.
- Look for proficient students who understand the limitations of the tools that they are using.
Mathematical Practice 8: Look for and express regularity in reasoning.
- Look for students who make the connection between the properties of the diagonals of a parallelogram and the properties of the diagonals of a rectangle.
Challenge Problem
Answer
- Students need to apply the property that the diagonals of a rectangle bisect each other and have the same length. Students solve the Challenge Problem by drawing two segments that have the same length and bisect each other. They connect the endpoints of the segments to form a rectangle.
Work Time
Prepare a Presentation
- Explain what you learned about parallelograms and their diagonals and angles. Support your thinking with examples of your work.
Challenge Problem
- Can you draw a rectangle using a method that is different from the one you just used? If yes, explain your method.
Make Connections
Ways of Thinking
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson. Ask questions such as the following:
- On your sheet of paper, which angles are congruent? What can you call these congruent angles? Do you think this will always be true in parallelograms?
- Which angles are supplementary? What can you call these supplementary angles? Do you think this will always be true in parallelograms?
- What is the sum of the angle measures in a parallelogram?
- If you had a ruler and a protractor, how could you draw parallel lines?
- Do you think that the diagonals in a parallelogram will always divide each other in half? (You can informally introduce the term bisect.)
- How is a rectangle the same as a parallelogram? How is a rectangle different from a parallelogram? (Make sure diagonals are discussed.)
- What other properties do you know about parallelograms?
- How did [students] organize their thoughts differently? Which makes more sense to you? Which brought out the structure of the mathematics?
- How did [students] make sense of the problems?
- Can you state what [students] said in a different way?
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' explanations of the angles and diagonals in parallelograms.
Hint:
As your classmates present, ask questions such as:
- Why are the opposite angles congruent and the adjacent angles supplementary? Do you think this will always be true for parallelograms?
- What is the sum of the angle measures in a parallelogram?
- Do you think that the diagonals in a parallelogram will always divide each other in half?
- How is a rectangle related to a parallelogram? How is it different?
Parallelograms
A Possible Summary
In a parallelogram, opposite sides are congruent and parallel. Opposite angles are congruent, and adjacent angles are supplementary. The diagonals of a parallelogram divide each other into two equal segments. In a rectangle, they are congruent; in a square, they are both perpendicular and congruent. The sum of the angle measures in any quadrilateral is 360°.
SWD: When summarizing the properties of parallelograms and their diagonals, provide a diagram with all angle measures included in the diagram. Make sure that you provide definitions, and have all students record this information.
Formative Assessment
Summary of the Math: Parallelograms
Write a summary about the angles and diagonals in a parallelogram.
Hint:
Check your summary:
- Do you explain the relationship between the opposite angles and adjacent angles in a parallelogram?
- Do you say what the sum of the angle measures in a parallelogram is?
- Do you explain the relationship between the diagonals in a parallelogram?
- Do you explain the differences between a rectangle and a parallelogram?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students have learned about the angles and diagonals of parallelograms and rectangles.
ELL: ELLs may need support as they respond in writing about the angles and diagonals of parallelograms and rectangles. Allow them to sketch diagrams or to speak with other students in their language of origin. Emphasize the content of their writing over concerns about grammar, spelling, or punctuation. When addressing these areas, choose just one issue.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I wonder about parallelograms is …