Review Quiz

Overview
Students critique and revise their work from the Self Check after receiving feedback. Students then take a quiz to review the goals of the unit.
Key Concepts
Students reflect on their work and apply what they've learned about the characteristics of geometric figures.
Goals and Learning Objectives
- Critique and revise work on the Self Check.
- Apply skills learned in the unit.
- Understand the relationship of angles:
- Created by intersecting lines.
- Found in quadrilaterals, triangles, and polygons.
Critique
Lesson Guide
Return students' solutions to the Self Check task. If you have not added questions to individual pieces of work, write your list of questions on the board now. Students can then select questions appropriate to their own work.
Give students a few minutes to read over the feedback and to review the questions in the opening of the lesson.
ELL: Provide ELLs and other students a sample or model for the concepts, strategies, and applications that will be addressed in the Assessment, and the format you want them to follow. Be prepared to address and explicitly re-teach or review vocabulary, concepts, strategies, and applications.
Opening
Critique
Review your work on the Self Check problem and think about these questions:
- What are the sums of the angle measures in different polygons?
- How can you find the measure of ∠FGE?
- What angle does ∠BGC and ∠CGE form?
- What do you know about the angles formed by two intersecting lines?
- Find a different way of solving the problem.
- What do you know about the angles in parallelograms, triangles, and other polygons?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will apply what they know about the characteristics of geometric figures in order to find missing angles and identify types of polygons.
Opening
Apply what you know about geometric figures in order to find missing angles and identify types of polygons.
Revise Your Work
Lesson Guide
Have students work in pairs to revise their work and to critique their partner’s solution.
SWD: Some students with disabilities may struggle with self-assessment; use your knowledge of student strengths and vulnerabilities to inform and create interventions you will put into place for this period of class time.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
In critiquing their solution to the Self Check task, students must understand another person’s reasoning, recognize and analyze errors in their work, and articulate ways of improving the work.
Mathematical Practice 5: Use appropriate tools strategically.
Look for students who model the problem(s) with drawings or who ask to use other tools.
Interventions
Student has difficulty getting started.
- What do you already know?
- What do you need to know?
- What is the sum of the angle measures in a triangle?
- How is this related to angle sums in other polygons?
Student has an incorrect solution.
- Have you checked your work?
- Does your answer make sense?
Student has a solution.
- Can you explain how you solved the problem?
- Is there another way to solve it?
Student believes that a quadrilateral is a parallelogram.
- Show a counterexample.
- What are the properties of parallelograms?
Possible Answers
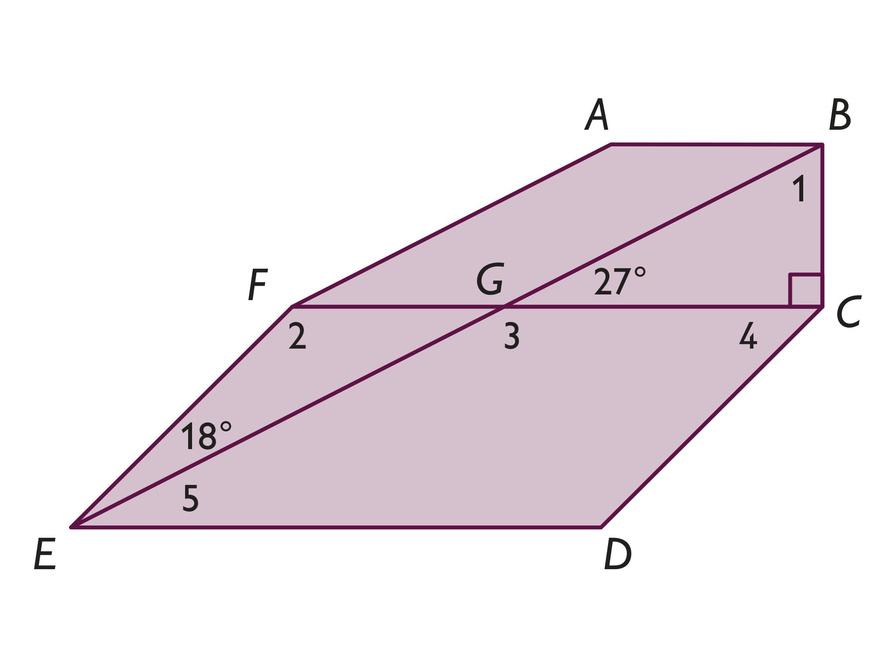
The measure of ∠1 is 63°.
The measure of ∠2 is 135°.
The measure of ∠3 is 153°.
The measure of ∠4 is 45°.
The measure of ∠5 is 27°.- Solutions will vary. Students may use the following concepts to find the angle measures:
• Complementary angles to find m∠1
27° + m∠1 = 90°
m∠1 = 63°
• The angle sum of a triangle is 180° to find m∠2 (and m∠1).
18° + 27° + m∠2 = 180°
m∠2 = 135°
• Supplementary angles to find m∠3
27° + m∠3 = 180°
m∠3 = 153°
• Consecutive angles of a parallelogram are supplementary to find m∠4.
m∠2 + m∠4 = 180°
135° + m∠4 = 180°
m∠4 = 45°
• Opposite angles of a parallelogram are congruent to find m∠5.
18° + m∠5 = m∠4
18° + m∠5 = 45°
m∠5 = 27°
- The sum of the angles in the hexagon is 720°. There are 6 sides, so use the general rule:
s = (6 − 2)180°
s = 4⋅180°
s= 720°
Students could also add together the measures of each of the angles of the hexagon angles to find the sum.
Work Time
Revise Your Work
Work with your partner to revise your work on the Self Check problem based on the questions from the Opening and feedback from your partner.
ABGF andCDEF are parallelograms.
- Find the measures of ∠1, ∠2, ∠3, ∠4, and ∠5.
- Explain how you determined each angle measure.
- What is the sum of the angles in the hexagon? How do you know?
Figure Game
Lesson Guide
Have students work with a partner to play the game. After playing the game several times, have the partners discuss their strategies.
ELL: When students work in pairs, teachers can monitor individual student progress by listening and recording student conversations and peer problem solving. This type of collaborative work gives ELLs the opportunity to use mathematical language and to engage in conversation with their peers. Allow students to speak in their language of origin if it helps them ask good questions about the type of polygon.
Possible Answers
- Here are some sample questions that should narrow down the choices:
- Does the figure have congruent sides?
- Does it have four sides?
- If the figure has four sides, does it have any parallel sides?
- The questions that students ask are part of the strategy. Some students will ask questions with a figure in mind, rather than asking questions that will eliminate possibilities.
Work Time
Figure Game
Play the following game with a partner:
- Draw a figure on a sheet of paper, but do not show the figure to your partner. (Draw a figure such as a rhombus, an isosceles right triangle, a regular polygon, and so on.)
- Your partner needs to determine what shape you drew by asking yes-or-no questions. Your partner should not try to guess the shape until sure that only the one shape is possible.
- Once your partner guesses the figure, switch roles.
After you play the game several times, consider these questions:
- What strategies did you use?
- What types of questions were particularly helpful?
Hint:
- What do you know about the sum of the angle measures in different figures and how the angles in different figures are related?
- What characteristics define different figures?
Prepare a Presentation
Preparing for Ways of Thinking
While students work with their partner, notice the following responses to discuss in the Ways of Thinking task:
- Different student approaches to the task
- The problem-solving approaches that students choose
Notice students' mathematical decisions:
- Do they track their progress in use of the mathematics?
- Do they notice if they have chosen a strategy that does not seem to be productive? If so, what do they do?
- Do they use the properties of supplementary angles, consecutive angles, and opposite angles in a parallelogram?
- Do students apply the sum of angles for different polygons?
- Do students understand conditions that create triangles and use appropriate tools to check conditions?
Challenge Problem
Answers
- Students can draw any type of polygon.
- Some questions that students could ask each other to help narrow down the shape are:
- How many angles are there?
- How many diagonals could you draw?
- Does the sum of angles add up to 180°? 360°? 540°? More?
- Are the opposite angles congruent?
- Are the adjacent angles supplementary?
- Are the diagonals congruent?
- Are the diagonals bisected?
- Are all sides congruent?
- Are all angles congruent?
- Students will switch roles and their partner will draw a shape to be guessed.
Work Time
Prepare a Presentation
Explain how you revised your work, and why you felt the revisions were necessary. Give examples of the types of mistakes you made.
Challenge Problem
- Play the same type of game by drawing a figure on a sheet of paper, but do not show the figure to your partner.
- This time your partner needs to determine what shape you drew by asking yes-or-no questions but can’t be about the number of sides—the questions must be about the diagonals, the angles, or other features of the figure. Your partner should not try to guess the shape until sure that the answer is the only shape possible.
- Once your partner guesses the figure, switch roles.
Make Connections
Ways of Thinking
Organize a whole group discussion to consider issues arising from the work students did to revise their work. You may not have time to address all these issues, so focus the discussion on the issues most important for your students. Ask students the following questions:
- How did you justify each step?
- Did you try any strategies that did not work? If so, why didn't they work?
- Which angle was the most difficult to find? Why?
- What part of the task was most difficult?
- What characteristics define different figures?
- How are the angles in different figures related?
- Did you and your partner ever disagree about a solution or about how to revise your work? Did you resolve your disagreement? How?
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' revisions of the Self Check problem.
Hint:
As your classmates present, ask questions such as:
- Did you try any strategies that did not work? If so, why didn’t they work?
- Which angle was the most difficult to find? Why?
- What is your justification for each step?
- What part of the task was the most difficult?
- Did you and your partner ever disagree about a solution or about how to revise your work? Did you resolve your disagreement? How?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to determine what students believe about quadrilaterals and other polygons with more than three sides have in common.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Quadrilaterals and other polygons with more than three sides have several things in common with triangles, such as …