- Author:
- Chris Adcock
- Subject:
- Geometry
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Cube from Parallelograms
Exploring Quadrilaterals
Exterior Angles of Polygons
More Angles: Intersecting Lines
Paper Folding
Parallelogram Diagonals
Perpendicular Diagonals
Ratios and Angles
Trapezoids
Gallery Problems Exercise

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit’s concepts or to assist students who may have fallen behind on work.
Problem Descriptions
Parallelogram to Cube
Students have a chance to review angle measurements in a parallelogram. Building the cube helps students see the transition from two-dimensional shapes and their relationship to three-dimensional figures.
Quadrilaterals
Students investigate the possible quadrilaterals that can be made from any four given side lengths, focusing on those that can’t make a quadrilateral. Students also look at possible parallelograms with two sides given and possible rhombuses with four sides given.
Diagonals
Students further investigate diagonals in quadrilaterals. If the diagonals are perpendicular, is the figure a rhombus?
Trapezoids
How many right angles can a trapezoid have? How many congruent angles or congruent sides can it have? Can its diagonals be perpendicular or congruent? Students investigate possible trapezoids.
More Angles
Students explore three intersecting lines and the combinations of angles.
Diagonals and Angles
The sides of a parallelogram are extended beyond the vertices, and students explore which angles are congruent and which are supplementary. Students also explore the effect diagonals have on interior angles.
Exterior Angles
Students explore the sum of exterior angles for several polygons and speculate about the results.
Angles and Sides
Students explore the relationship between angles and sides in a triangle and discover that the longest side is opposite the largest angle, and the shortest side is opposite the smallest angle (and congruent sides are opposite congruent angles).
Ratios and Angles
Students explore the ratios of the legs of a right triangle to the angles in the triangle. Students see that there is a unique ratio for each angle, and vice versa. This is an informal look at trigonometry.
Find the Angle
Students solve equations to find angle measures in polygons.
Tessellations
Students explore quadrilateral tessellations and why they tessellate. Students also explore tessellations of pentagons and other polygons.
Parallelogram to Cube
Possible Answers
Part 1
- This problem gives students a chance to review angle measurements in a parallelogram. Building the cube helps students see the transition from two-dimensional shapes and their relationship to three-dimensional figures.
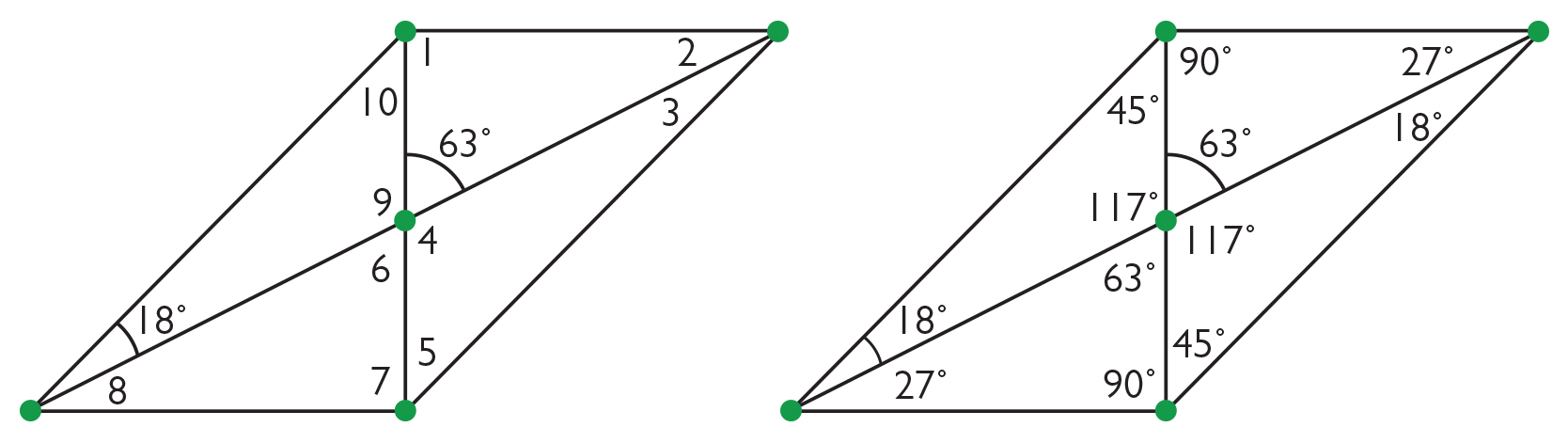
- Angles in the parallelogram:
The measures of angles 1 and 7 are both 90° because the paper was folded this way.
The measure of angle 6 is 63° because it is the vertical angle to the given angle.
The measures of angles 2 and 8 are both 27° because this is the complementary angle to 63° in the right triangle (27° + 63° = 90°).
The measures of angles 4 and 9 are both 117° because they are supplementary to 63° (117° + 63° = 180°).
The measure of angle 10 is 45° because 18° + 117° + 45° = 180°, but also because a corner (90°) was folded in half.
The sum of the measures of angles 1 and 10 form an angle of the parallelogram. The angle opposite is congruent, so the measure of angle 5 is also 45° (and because of the same fold).
The sum of the measures of the lower left angles is 45°, so the sum of the measures of the upper right angles opposite is also 45°, and the measure of angle 3 is 18°. Notice the large right triangles are isosceles (from the fold down), so the two angles are congruent and complementary (both 45°).
Part 2
- Students may choose to make a cube individually or in a group.
Work Time
Parallelogram to Cube
Part 1
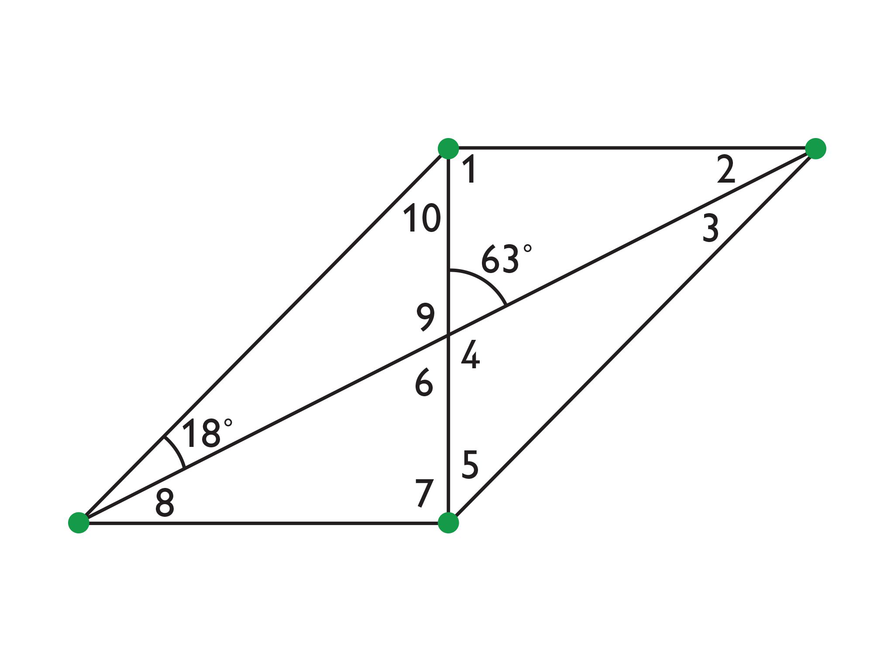
- Watch the video about folding a parallelogram again and fold a second parallelogram.
- Given the two angle measures shown, what are the measures of the other angles in the parallelogram?
VIDEO: Paper Folding
Part 2
- The parallelograms can be assembled to form a cube. You need six parallelograms, so either make four more or combine yours with two other students’ to get six parallelograms.
- Watch the second video to see how the cube is constructed. Think about the angles involved in changing the two-dimensional figures into surfaces for a three-dimensional figure.
- Make 5–6 cubes if you want to use them in the Zooming in on Shapes unit.
VIDEO: Cube from Parallelograms
Quadrilaterals
Possible Answers
In this problem, students go through an investigation similar to the one they did with triangle side lengths. They will apply some of the same reasoning to see what conditions make quadrilaterals.
- Students are free to explore different conditions, but only three short sides and one long side will not work.
- The only condition that will not allow a quadrilateral is if the sum of the lengths of three sides is shorter than the length of the fourth side.
- Given one or two side lengths:
- If one side length is given, then the opposite side length is known, but there are still an infinite number of parallelograms because the other pair of sides can be any length.
- If two side lengths are given for sides that are opposite each other, then it would be the same situation as problem (a), and an infinite number of parallelograms can be formed. However, if the two sides are not opposite, then all four side lengths are given (because the opposite sides have to be congruent). But, there are still an infinite number of parallelograms that can be made because the angle measures can be different when the side lengths are known.
- If the length of one side of a rhombus is given, all side lengths are given because they are all congruent. However, there are still an infinite number of possible rhombuses, because the angles can change.
Work Time
Quadrilaterals
- Explore the side lengths of different quadrilaterals.
- What happens if there is one short side or two short sides?
- What happens if three sides are long and one is short?
- What if three sides are short and one is long or if all four sides are short?
- What conditions will not allow a quadrilateral to be formed?
- Answer the following:
- If the quadrilateral is a parallelogram, and one side length is given, how many parallelograms can be formed?
- How many can be formed if two side lengths are given?
- If the quadrilateral is a rhombus, how many rhombuses can be formed if one side length is given?
HANDOUT: Exploring Quadrilaterals
Diagonals
Possible Answers
- In this problem, students further investigate diagonals in quadrilaterals. At this point they may believe that if the diagonals are congruent and perpendicular, the figure is a square, and if the diagonals are perpendicular, it is a rhombus. However, these conditions are true only if the figure is a parallelogram.
The sketch shown is the case of perpendicular diagonals. Students will find that the diagonals still define a rhombus if they bisect each other.
- A quadrilateral can be formed, but perpendicular diagonals are not a defining characteristic of all quadrilaterals.
- A trapezoid can be formed, but perpendicular diagonals are not a defining characteristic of all trapezoids.
- A rhombus can be formed, with bisecting diagonals; perpendicular diagonals are a defining characteristic of all rhombuses.
- A square can be formed with congruent and bisecting diagonals; perpendicular diagonals are a defining characteristic of all squares. A rectangle (generally) cannot be formed. (While rectangles with four equal sides—that is, squares—have perpendicular diagonals, any rectangles without four equal sides will not have perpendicular diagonals.) Perpendicular diagonals are not a defining characteristic of rectangles.
The conclusion is that perpendicular diagonals do not define all parallelograms, trapezoids, and quadrilaterals, but that these shapes may still have perpendicular diagonals. Perpendicular diagonals are a defining characteristic of rhombuses, kites, and squares, but just because a figure has perpendicular diagonals, it does not mean that it must be a rhombus, kite, or square. Students could further investigate congruent diagonals, and see that they don’t define anything unless they bisect each other (in which case, they define a rectangle).
Work Time
Diagonals
- Explore Perpendicular Diagonals in quadrilaterals.
- What figures can have perpendicular diagonals?
- A quadrilateral
- A trapezoid
- A rhombus
- A square
- A rectangle
- What can you conclude about figures with perpendicular diagonals?
HANDOUT: Perpendicular Diagonals
Trapezoids
Possible Answers
- The quadrilateral explorations in the unit focused on parallelograms. This problem gives students a chance to learn a little more about the properties of trapezoids.
- A trapezoid can have two right angles, if they are consecutive angles. If there are three right angles, then the second pair of sides become parallel, and the figure is a rectangle.
- There can be two congruent sides; they can be consecutive sides or opposite sides (in which case, the trapezoid is isosceles). There can be three congruent sides, and again, the trapezoid will be isosceles. If the opposite sides (legs) between the parallel bases are congruent, the diagonals are also congruent.
- The diagonals can be perpendicular. If the diagonals are congruent, the opposite sides (legs) between the bases are congruent. The base angles will be congruent, and the top-side angles will be congruent (the two angles by either the left or right side are supplementary).
- Trapezoids can have congruent sides and right angles. They can have perpendicular or congruent diagonals (but not both). The one special trapezoid is the isosceles trapezoid, which has congruent diagonals and two congruent pairs of angles.
Work Time
Trapezoids
Investigate various trapezoids for the given conditions.
- Explore different trapezoids.
- How many right angles can a trapezoid have? Why?
- Can there be two or three congruent sides? Can opposite sides be congruent? If so, what do you notice?
- Can the diagonals be perpendicular? Can the diagonals be congruent? If the diagonals are congruent, what do you notice about the trapezoid’s angles?
- What can you conclude about possible trapezoids?
HANDOUT: Trapezoids
More Angles
Possible Answers
- This problem shows students that vertical and supplementary angles are still present if more than two lines intersect.
- The angle sum around any point will be 360° because this is a full circle.
- The pairs of congruent angles are opposite each other, and their rays are coming from the same two lines.
- The measures of any three consecutive angles will add up to 180°. Since opposite angles are congruent, a set of every other angle will also add up to 180° (there are two such groups of angles).
- Yes. If any two adjacent angle measures are added, their sum will be equal to the two opposite angle measures’ sum.
- There cannot be exactly three congruent angle measures because the angles opposite are congruent. Two of the congruent angles could be one pair of vertical angles, but the third angle would have a congruent opposite angle (so, exactly four is possible). Five is not possible for similar reasons. Six is possible, and each angle would measure because .
- The same relationships exist for more than two intersecting lines: there are still supplementary angles and vertical angle combinations.
Work Time
More Angles
- Draw three lines that intersect at the same point.
- What do you think the sum of all the angle measures will be? Measure all the angles.
- Which angles are congruent? How are they similar to vertical angles?
- Which angle measures will add to 180°?
- Can the sum of a pair of angle measures be equal to another pair of angle sums?
- Can three, four, five, or six angles be equal?
- What can you conclude about angles formed by three intersecting lines?
HANDOUT: More Angles: Intersecting Lines
Diagonals and Angles
Possible Answers
This investigation allows students to explore properties of diagonals in parallelograms further, particularly looking at the effect the diagonals have on the interior angles.
- The angles opposite each other, on opposite sides of the diagonal, are congruent. For example, is congruent to . The diagonals divide the parallelogram into four triangles. Students may see that there are two pairs of congruent triangles because of the congruent angles and congruent vertical angles. The sides are congruent because opposite sides of the parallelogram are congruent and the diagonals bisect each other.
- For the divided angles to be congruent (bisected), the angle of the diagonal intersection will be 90° and the sides of the parallelogram will be congruent. In other words, the figure will be a rhombus (possibly a square).
- The diagonals of a parallelogram divide the interior angles into a pair of angles that have congruent partners at the other end of the diagonal. If the angle is divided evenly (bisected), then the parallelogram is a rhombus (possibly a square).
Diagonals and Angles
Look at the parallelogram example to answer the questions.
- What do you notice about the angle measures that are created by the diagonals?
- What shape would you have if each pair of angles at the vertices were congruent?
- What can you conclude about the angles formed by the diagonals of a parallelogram?
HANDOUT: Parallelogram Diagonals
Exterior Angles
Possible Answers
Students have explored the interior angle sum for polygons and discovered a general rule. That knowledge will be applied to find the angle sum for exterior angles, and to understand why it is 360°.
- Answers will vary, but some students may see that it will be 360°.
- Students will see that the exterior angle sum is 360° in each case and speculate that it will be true for all polygons. Using the vertex of each exterior angle as a common vertex, the angles will fit together to form 360° because consecutive exterior angles share a common side, treating them as adjacent angles.
The sum of the measures of the exterior angles of a quadrilateral is as follows:
Rearranging the values:
Using the formula for the sum of the interior angles of an n-sided polygon, , the sum of the measures of the interior angles is .
If the polygon had more sides, 180° would be multiplied by the number of sides, but 2 less than the number of sides multiplied by 180° would be subtracted, leaving 2 multiples of 180°, or 360°. If n is the number of polygon sides:
Work Time
Exterior Angles
Look at the exterior angle measurements for each polygon.
- Draw a pentagon, a hexagon, and an octagon. What do you think the sum of the exterior angles will be on each polygon? Measure each angle and check.
- What do you notice about the exterior angle sum for each polygon? Do you think this will be true for all polygons?
- Looking at the angles mathematically, what is the sum of the measures of exterior angles in terms of the interior angles?
For example, if the quadrilateral angles are labeled a, b, c, and d, the exterior angles are , , , . What is the sum of the measures of angles a, b, c, and d? - What can you conclude about the sum of exterior angle measures in polygons?
HANDOUT: Exterior Angles of Polygons
Angles and Sides
Possible Answers
Students have looked at angles and sides in triangles as defining characteristics, but they haven’t had the opportunity to look at the relationship between the two. Students have an idea that there is a relationship, as they have seen that isosceles triangles have two congruent sides and angles, and equilateral triangles have three congruent sides and angles.
Comparing sides to the angles opposite them:
- The longest side of the triangle is opposite the largest angle.
- The shortest side is opposite the smallest angle.
- The middle-length side is opposite the middle-size angle.
- Students will see that this relationship is always true (as much as they can “infinitely” manipulate the sketch). They can see that as a side is longer, it spreads the angle opposite wider, and as the side is shorter, the angle opposite is narrower.
- If two or three sides are congruent, the angles opposite will be congruent.
- If the triangle is a right triangle, the side opposite (the hypotenuse) will always be the longest side. Because the other two angle measures add up to 90° they will be smaller angles than the right angle.
Work Time
Angles and Sides
Look at the two triangles provided. Only one vertex differs between the two.
- How do the angle measures compare to the side lengths they are opposite to?
- Which angle is opposite the longest side: the smallest, largest, or middle-size angle?
- Which angle is opposite the shortest side: the smallest, largest, or middle-size angle?
- Which angle is opposite the middle-length side: the smallest, largest, or middle-size angle?
- Do you think these relationships will always be true? Draw another triangle and see.
- What happens to the angle measures if two or three sides are congruent?
- What happens if one angle is a right angle?
HANDOUT: Angles and Sides
Ratios and Angles
Possible Answers
- As students begin to see that there is a relationship between the side lengths and the size of the angles in a triangle, the next step is to look at the ratio of side lengths for given angles. Students get a sneak preview of trigonometry and see that angles in triangles have specific ratios.
- Students should see that the angle measure doesn’t change. Changing the side lengths, but maintaining the ratio, produces a similar triangle.
- The same process works both ways: if the angle stays the same, the ratio stays the same. The triangle is just larger or smaller.
- As the ratio increases, the angle measure increases and vice versa. Students may notice that the ratio approaches infinity and is in fact undefined if leg is zero.
- There is a unique ratio for each angle measure, and it increases as the size of the angle increases.
Work Time
Ratios and Angles
- Draw a right triangle. Label it ABC. The right angle should be at C. Find the ratio of the sides that include the right angle by dividing AC by CB.
- Choose leg lengths for the triangle and note the ratio and angle measure. Change the size of the triangle so that it still has the same ratio (for example, if the ratio was = you could change it to = . What do you notice about the angle measure?
- Choose leg lengths for the triangle and note the ratio and angle measure. Change the size of the triangle so that it still has the same angle measure. What do you notice about the ratio?
- What is the relationship between the ratio and the angle measure? In other words, how does the angle size change as the ratio changes (or how does the ratio change as the angle size changes)?
- What can you conclude about the relationship of the ratio of the leg lengths of a right triangle to the measure of angle B ?
HANDOUT: Ratios and Angles
Find the Angle
Possible Answers
This problem gives students the opportunity to work on Mathematical Practice 3: Construct viable arguments and critique the reasoning of others. Students create problems with a missing angle measure to solve for. Students need to think about how much information is necessary, without giving unneeded information.
- Answers will vary.
- Answers will vary, but students should see that for the case of a parallelogram, only one angle measure is needed.
Work Time
Find the Angle
- Create problems for a partner to solve where an angle measure is missing. You can make up the problem based on your knowledge of angles in geometric shapes or you can draw figures with a ruler and protractor to create a problem.
- Create a problem for a triangle, quadrilateral, and another polygon. Think of how much information you need to include, but don’t give unneeded information.
Tessellations
Possible Answers
Part 1
This investigation leads students to see the relationship of the angles in quadrilaterals and triangles and those same angles arranged around a point.
- Tessellation with six regular polygons around each point:
- Interior angles: 60°.
- The regular polygon is a triangle. It has 3 sides.
Tessellation with three regular polygons around each point:
- 120°
- The regular polygon is a hexagon. It has 6 sides.
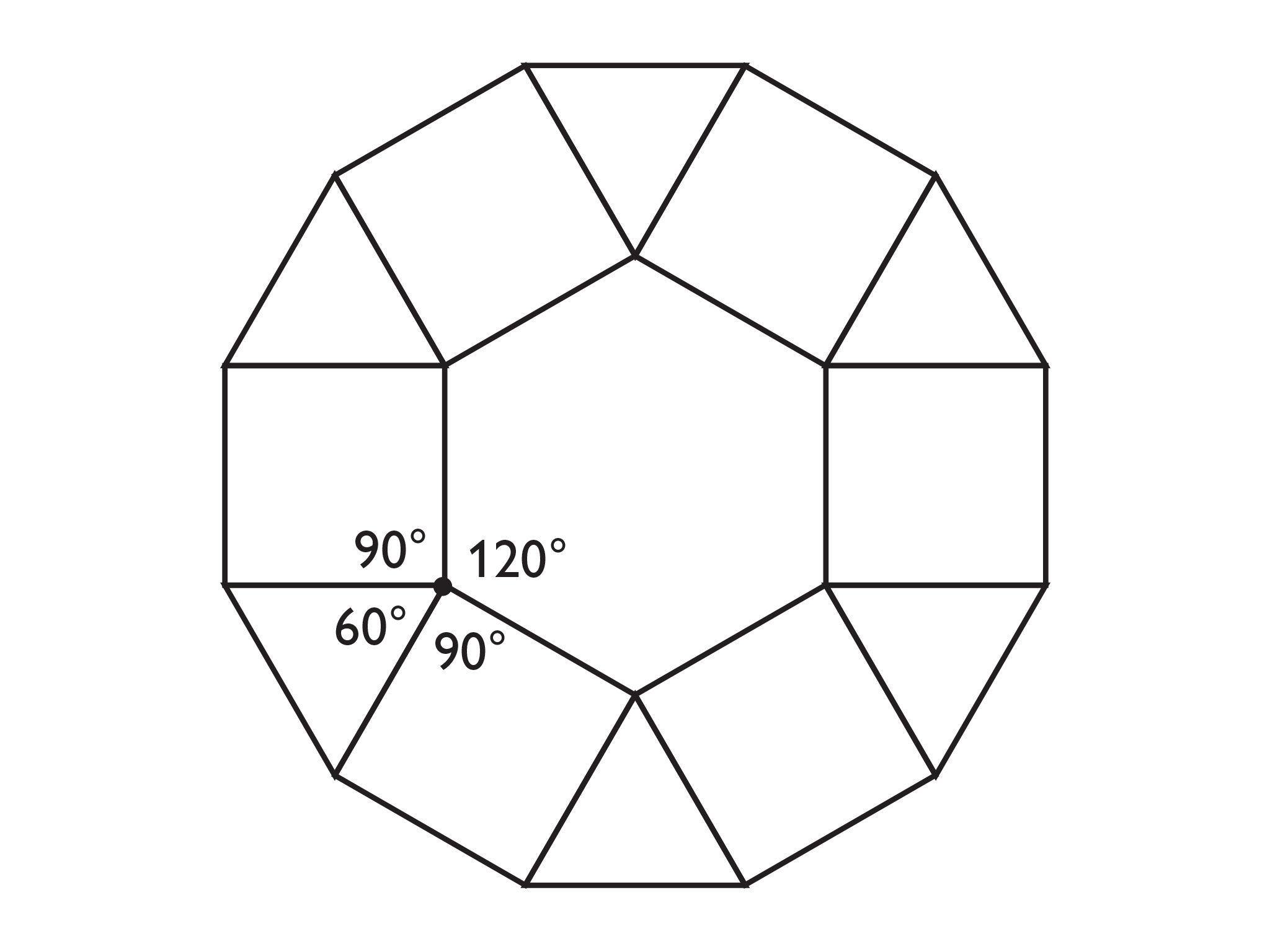
Semi-regular tessellation with four regular polygons around each point:
- 120°, 90° (2 of them), 60°
- The regular polygons are one hexagon (six sides), two squares (four sides each), and an equilateral triangle (three sides)
- 120°, 90° (2 of them), 60°
Two regular octagons and one square around each point:
- The two polygons (octagon and square) tessellate because they can be arranged so that the angle sum around a point is 360°.
- Sketches will vary.
- Answers will vary. Any polygon can tessellate if it can be constructed so that the sum of the angle measures around any given point is 360°. Some possible answers for regular tessellations are 4 squares, 6 triangles, or 3 hexagons. Some possible answers for semi-regular tessellations are 2 pentagons and 1 decagon, 2 hexagons, and 2 triangles, or 1 hexagon and 4 triangles.
Work Time
Tessellations
Part I
If the angles that form a complete circle around a vertex are the interior angles of regular polygons, then those polygons can form the basis of a repeating pattern called a tessellation.
The first two images use regular polygons. This pattern is called a regular tessellation.
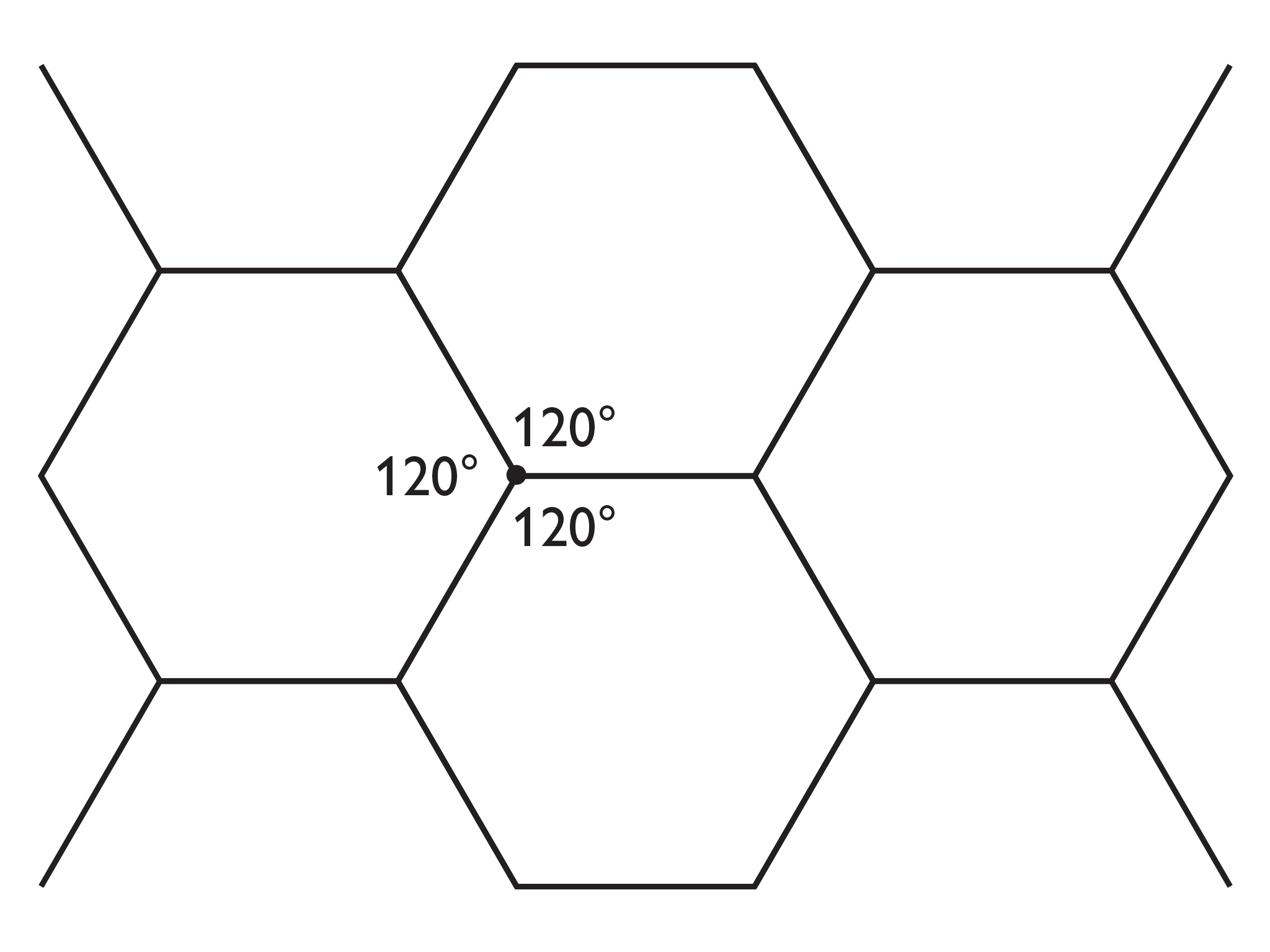
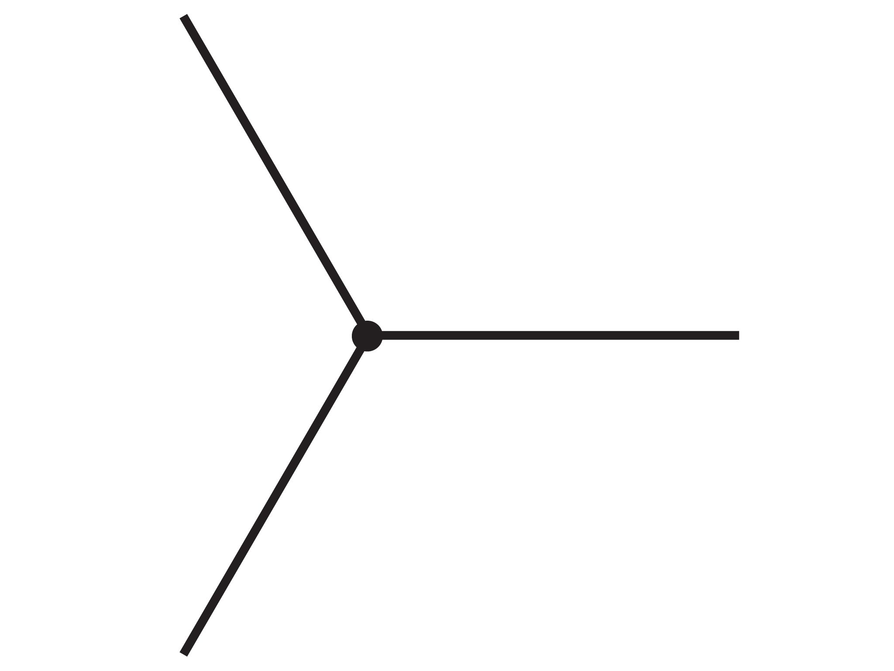
- A regular tessellation is made using six regular polygons around each point.
- What is the measure of an interior angle of that regular polygon?
- How many sides does that regular polygon have?
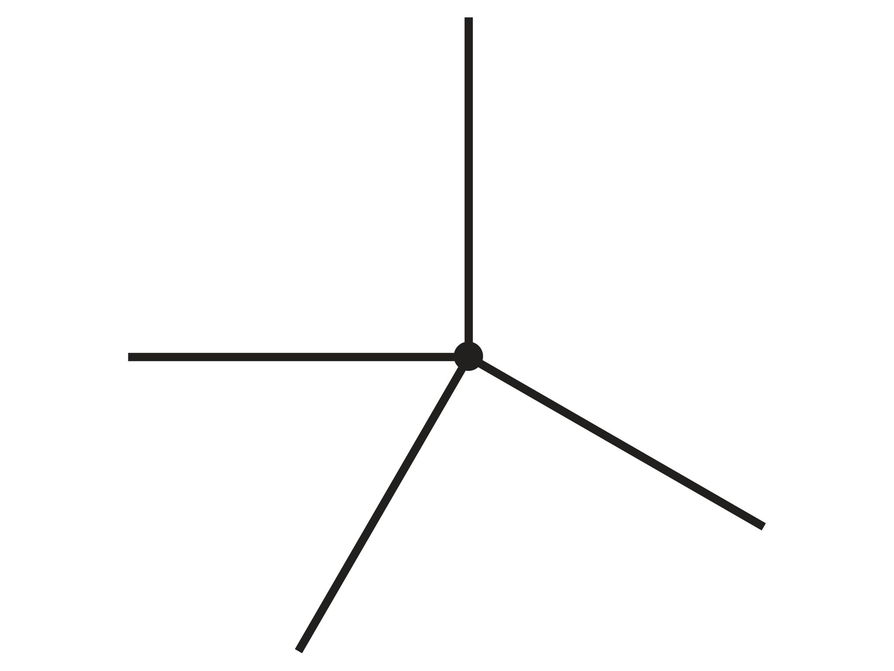
- A regular tessellation is made using three regular polygons around each point.
- What is the measure of an interior angle of that regular polygon?
- How many sides does that regular polygon have?
Part 2
The second pattern is called a semi-regular tessellation, because it uses more than one type of regular polygon.
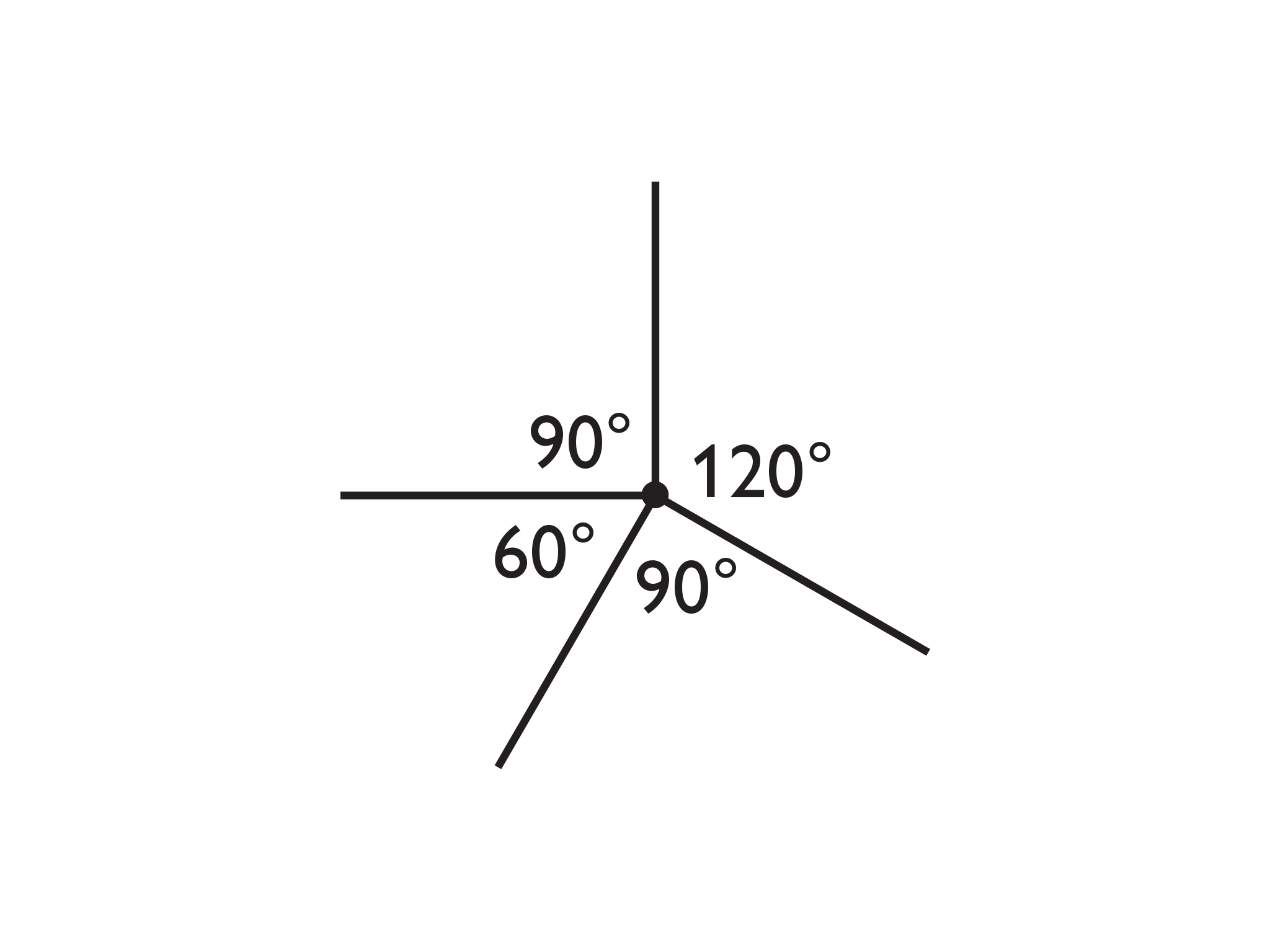
- A semi-regular tessellation is made using four regular polygons around each point.
- What is the measure of an interior angle for each regular polygon?
- How many sides does each regular polygon have?
- It is possible to arrange two regular octagons and one square around one point.
- Explain why.
- Sketch a part of the semi-regular tessellation that is produced by this arrangement.
- Work with your partner to create a list of as many regular and semi-regular tessellations as you can.