Tape Diagrams

Overview
Students use tape diagrams to model relationships and solve problems about types of DVDs.
Key Concepts
Tape diagrams are useful for visualizing ratio relationships between two (or more) quantities that have the same units. They can be used to highlight the multiplicative relationship between the quantities.
Goals and Learning Objectives
- Understand tape diagrams as a way to visually compare two or more quantities.
- Use tape diagrams to solve ratio problems.
Introduction to Tape Diagrams
Lesson Guide
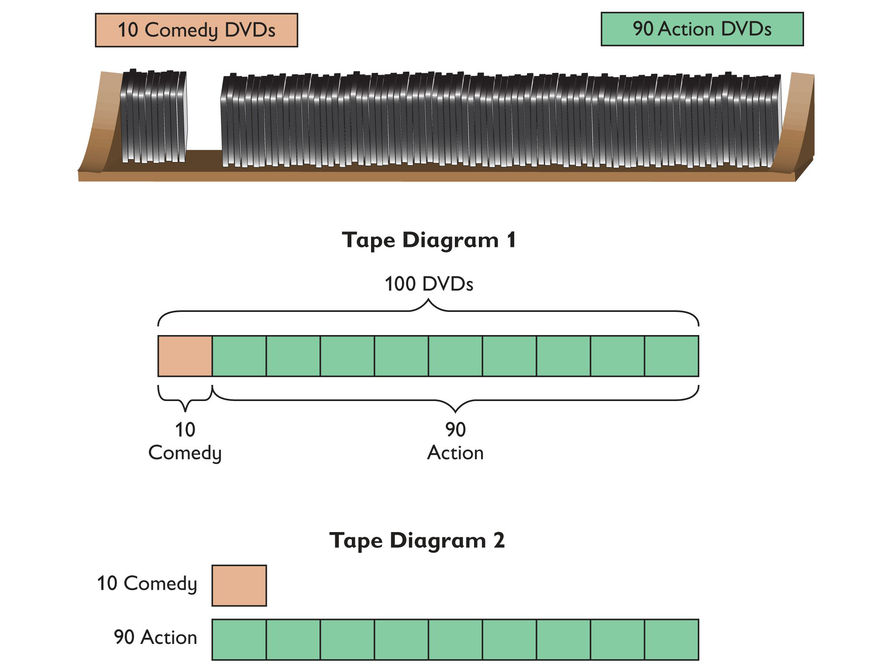
Review the problem and how the diagrams represent the situation. Answer the questions as a class. Students should conclude that the ratio of action DVDs to comedy DVDs is 9:1. The ratio of comedy DVDs to action DVDs is 1:9.
Mathematics
Two different tape diagrams are shown: one showing how many DVDs are represented by each unit of tape and the other showing just the ratios between comedy and action DVDs. Note that the first tape diagram, with the units of tape in direct sequence, shows both the part-part relationship and the part-whole relationships, whereas the second tape diagram emphasizes the part-part relationship.
Point out that the unit rectangles in tape diagrams are equal in length.
Opening
Introduction to Tape Diagrams
A store sells 10 comedy DVDs for every 90 action DVDs.
This relationship can be shown using a tape diagram. In the tape diagram, each unit (each square) represents 10 DVDs. There is 1 unit of comedy DVDs and 9 units of action DVDs.
There are different ways to arrange the tape diagram. You can see the ratio between the two quantities of DVDs more easily in Tape Diagram 2.
- What is the ratio of action DVDs to comedy DVDs?
- What is the ratio of comedy DVDs to action DVDs?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use tape diagrams to represent ratios and to solve problems about ratios.
Opening
Use tape diagrams to represent ratios and solve problems about ratios.
Carlos’s DVD Collection
Lesson Guide
Have students work in pairs on the problem about Carlos’s DVD collection.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students represent ratios as tape diagrams in order to represent and solve problems.
Mathematical Practice 6: Attend to precision.
Students may struggle with how best to communicate what the units represent on a tape diagram; prepare to build on these efforts in the Ways of Thinking discussion, with attention to the clarity and precision of explanations.
Interventions
Student doesn’t understand the problem about Carlos’s DVD collection because he or she misinterprets the tape diagram (e.g., thinks 1 unit of the given tape diagram represents 1 DVD).
- The tape diagram shows the ratio, not the actual values.
- Look back at the tape diagrams from the beginning of the lesson. How many DVDs does each unit represent?
- There are many possible pairs of values that have the ratio 5:2.
Possible Answers
- Carlos has 18 mystery DVDs.
- Solution methods may vary. Possible solution:
45 ÷ 5 = 9
9 ⋅ 2 = 18
Work Time
Carlos's DVD Collection
Carlos has a DVD collection. The ratio of action DVDs to mystery DVDs in his collection is 5:2. The tape diagram shows this ratio.
- If Carlos has 45 action DVDs, how many mystery DVDs does he have?
- Use the tape diagram to help you solve this problem.
Ask yourself:
- How many DVDs do 5 units in the tape diagram represent?
- How many DVDs does 1 unit in the tape diagram represent?
- How many DVDs do 2 units in the tape diagram represent?
Emma’s DVD Collection
Lesson Guide
Have students work in pairs on the problems and the presentation.
SWD: Some students with disabilities may need explicit instruction to create the tape diagram. Pull a small group. In advance, prepare a couple of ratio problems and their corresponding tape diagrams. Have the students match the tape diagram to the problem and then solve. Next, explicitly model creating a tape diagram with a new ratio problem. Now students can begin creating their own tape diagrams for subsequent problems.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students represent ratios as tape diagrams in order to represent and solve problems.
Mathematical Practice 6: Attend to precision.
Students may struggle with how best to communicate what the units represent on a tape diagram; prepare to build on these efforts in the Ways of Thinking discussion, with attention to the clarity and precision of explanations.
Interventions
In the problem about Emma’s DVD collection, the student makes a tape diagram that doesn’t represent the situation.
- Explain what your tape diagram shows to your partner.
- Where is the value “7” shown in your tape diagram? Where is the value “3” shown in your tape diagram?
- What is the number of DVDs per unit of your tape diagram?
Possible Answers
- Emma has 12 mystery DVDs.
28 ÷ 7 = 4
3 ⋅ 4 = 12
Work Time
Emma's DVD Collection
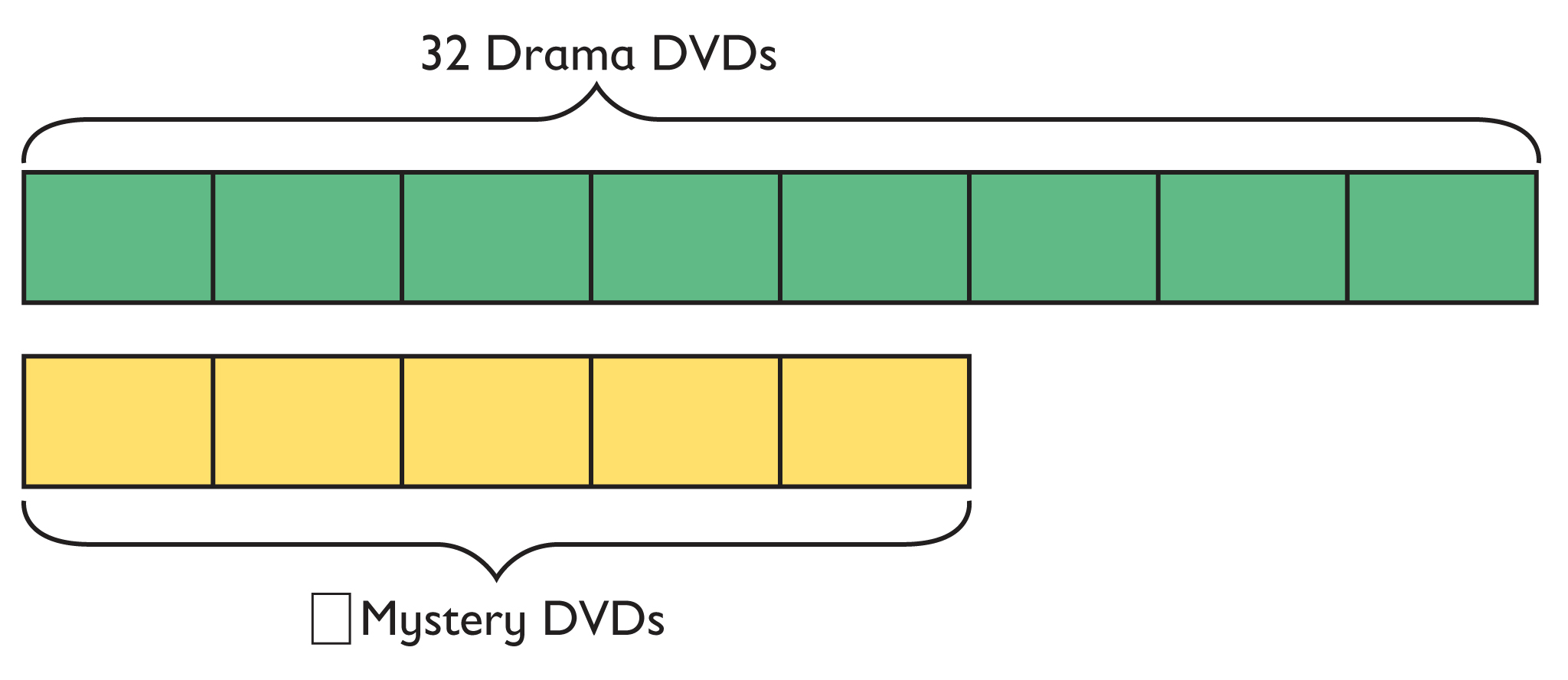
Emma has a DVD collection. The ratio of drama DVDs to mystery DVDs in her collection is 7:3.
- Make a tape diagram that represents the situation above.
- If Emma has 28 drama DVDs, how many mystery DVDs does she have? Use your tape diagram to find the solution.
Ask yourself:
- Create a tape diagram with two strips of tape.
- Create one strip of tape to represent the drama DVDs. How many units should you divide the strip into?
- How would you create a second strip of tape to represent the mystery DVDs?
- How many DVDs does each unit in your tape diagram represent?
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student thinking to highlight during the Ways of Thinking discussion:
- Students who debate about what the parts of a tape diagram represent, especially the units
SWD: A common issue for struggling students is not understanding what each part of the tape diagram represents. Have students reread the problem aloud, articulate their thinking, and then compare their tape diagram to a peer’s tape diagram. Comparing the diagrams will assist them in seeing any misconceptions they may have.
Challenge Problem
Possible Answer
- Emma bought 8 new mystery DVDs, giving her a total of 20 mystery DVDs in all.
Work Time
Prepare a Presentation
Explain how you made the tape diagram for Emma's DVD collection and how you used tape diagrams to help solve both problems.
Challenge Problem
Emma bought 4 more drama DVDs and some more mystery DVDs at a yard sale. The ratio of drama DVDs to mystery DVDs in her DVD collection is now 8:5.
- How many mystery DVDs did she buy? Draw a tape diagram and use it to solve this problem.
Make Connections
Mathematics
Focus the discussion on how students used the tape diagrams to solve the problems.
For Carlos’s problem, students should explain how the ratio 5:2 is shown in the tape diagram (as a length of 5 units compared to a length of 2 units). Students might also comment on the fact that the unit length on each tape is the same. Have students clarify how they figured out what each unit length represents.
For Emma’s problem, have students explain how the tape diagram they made represents the problem situation. Ask:
- What does the top tape represent? What does the bottom tape represent?
- Does your tape diagram represent a part-part relationship or a part-whole relationship? Explain.
- Where do you see the ratio 7:3 in the tape diagram?
- What does each unit represent? How do you know?
Have students who completed the Challenge Problem present their solution and discuss as a class.
ELL: Give students plenty of wait time as some of them are learning and processing new mathematical information in a second language. Write on a chart the key points that students make during their presentations.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
Frame the discussion as a collective effort to clarify and refine student explanations so that they are as precise as possible.
Performance Task
Ways of Thinking: Make Connections
Take notes about the different approaches your classmates used in making their tape diagram, and how students used the tape diagrams to solve the two ratio problems.
As your classmates present, ask questions such as:
- How did you determine the number of units to divide each strip of tape into?
- Could you have divided the tape into a different number of units?
- Can you explain how your tape diagram represents the ratio in the problem?
- Do you think using a tape diagram made it easier to solve the problem?
Tape Diagrams and Ratios
A Possible Summary
A tape diagram allows you to compare two amounts by representing each amount as a length, with both lengths divided into units of equal length.
Formative Assessment
Summary of the Math: Tape Diagrams and Ratios
Write a summary about how tape diagrams can be used to represent ratios and how they can be used to solve ratio problems.
Check your summary.
- Do you explain what a tape diagram is?
- Do you describe how a tape diagram can represent a ratio?
- Do you discuss how tape diagrams can be used to solve ratio problems?
Reflect On Your Work
Have each student write a brief reflection before the end of class. Review the reflections to find out how tape diagrams help students understand ratio.
ELL: Allow some additional time for ELLs to discuss their ideas with a partner before writing, in order to help them organize their thoughts. Allow ELLs who share the same native language to discuss in their preferred language and to use a dictionary.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Tape diagrams help me "see" ratios because ...