- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Gallery Problems

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery Descriptions
Work on Your Project
Students will work on their project with their group and evaluate their progress using the rubric.
Equivalent Ratios
Sometimes ratios that are equivalent don’t look equivalent at first. Students will use their ratio detective skills to identify equivalent ratios, and then they will choose a model to represent a set of equivalent ratios.
Three Farmers
Tough times on the farm mean three farmers are sharing a seed purchase. Students will make sure each farmer gets the right amount of seed.
The Dance
Everyone is excited about the upcoming school dance, and two students discuss the ratio of boys to girls. Students will evaluate their statements and decide if their statements are true.
The Adults at School
Who are the adults who work at school? Students will represent and investigate ratios of teachers to non-teaching staff, including adults at their own school.
Sports Reporters
Reporters are sometimes wrong. Students will check the math in two reports about soccer matches at Estadio Azteca in Mexico City.
Screen Challenge
The aspect ratio of movie screens and TV screens has a direct impact on viewers’ experience. Students will explore aspect ratios in this activity.
Election Results
Oops! A newspaper made an error in a report about the local election results. Students will find and fix the error.
Birthday at the Movies
Mia’s family is treating her whole class to a movie for her birthday! Students will calculate how much the tickets will cost.
Dinner Reservations
It’s graduation night! Students will calculate how many tables a restaurant needs for a party of 26 people.
Birth Months
Students will investigate the percent of students in a class who have birthdays in each month.
Work on Your Project
Students will work with their groups on their projects.
Work Time
Work On Your Project
- Work on your project with your group.
- Review the rubric to check that you have included everything in your project.
- Remember each project must contain:
- A written explanation that describes how you used ratios in your project
- At least one diagram or graph that shows how you used ratios in your project
- Accurate mathematical representations
Equivalent Ratios
Answers
The following two sets each consist of equivalent ratios:
Set 1: 2:5 40% 1:2 5:12 0.4
Set 2: 100:240 41.66666...%
- Answers will vary. Students can choose either set of equivalent ratios to represent using two different types of models (e.g., tape diagram, double number line, ratio table, or graph).
- Answers will vary.
- Students should share their models with a partner and refine them as needed collaboratively.
Work Time
Equivalent Ratios
Which of these ratios are equivalent?
a. 2:5
b. 100:240
c. 40%
d.
e. 1:2
f. 0.4
g.
h. 41.66666...%
i. 5:12Choose one of your sets of equivalent ratios in problem 1. Represent the set of equivalent ratios using one of these models:
- Tape diagram
- Ratio table
- Double number line
- Graph
Now choose another type of model to represent the same set of equivalent ratios you chose in problem 2.
- Share your models for problems 2 and 3 with a partner. Develop or refine your models as needed together.
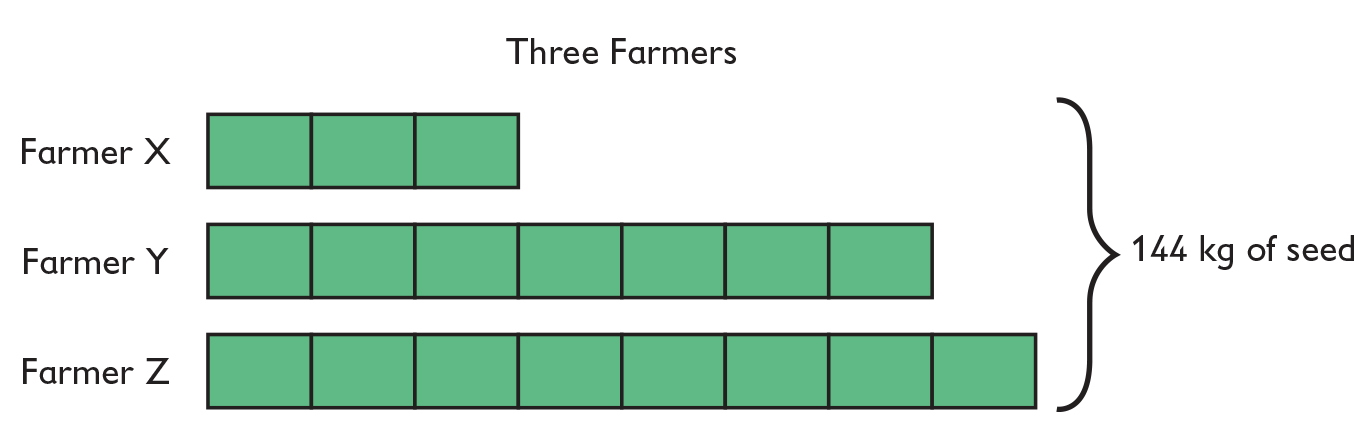
Three Farmers
Answers
- 18 units = 144 kg
144 ÷ 8 = 8, so 1 unit = 8 kg
Farmer X: 3 units • 8 kg = 24 kg
Farmer Y: 7 units • 8 kg = 56 kg
Farmer X: 8 units • 8 kg = 64 kg
Farmer X receives 24 kilograms of seed. Farmer Y receives 56 kilograms of seen. Farmer Z receives 64 kilograms of seed.
Work Time
Three Farmers
Together three farmers ( X, Y, and Z) buy seed for their farms and share it in the ratio 3:7:8.
- If they buy 144 kilograms of seed, how many kilograms of seed does each farmer receive?
- Show the problem solution using a tape diagram.
The Dance
Answers
- Yes, both Martin and Mia can be correct. Explanations will vary. Justifications should include diagrams. If 70 more girls than boys are coming and the ratio of boys to girls is 3:4, then 210 boys are coming and 280 girls are coming.
- a. Answers will vary. Possible answer: Using a ratio to compare two quantities can tell you how many girls there are “per boy”; using a difference comparison tells you how many more girls there are than boys at the dance. Neither comparison by itself gives you an actual count of people.
b. Answers will vary. Have students discuss and compare the merits of each choice for each situation.
Work Time
The Dance
Two students are discussing the upcoming school dance.
Martin says: “There are 70 more girls than boys coming.”
Mia says: “Yes, I heard that the ratio of boys to girls is 3 to 4.”
- Can both Martin and Mia be right? Use words and diagrams to justify your answer.
- Think about the two ways of comparing quantities.
a. Describe the advantages and disadvantages of each way.
b. Think of situations in which each way of comparing quantities would be useful.
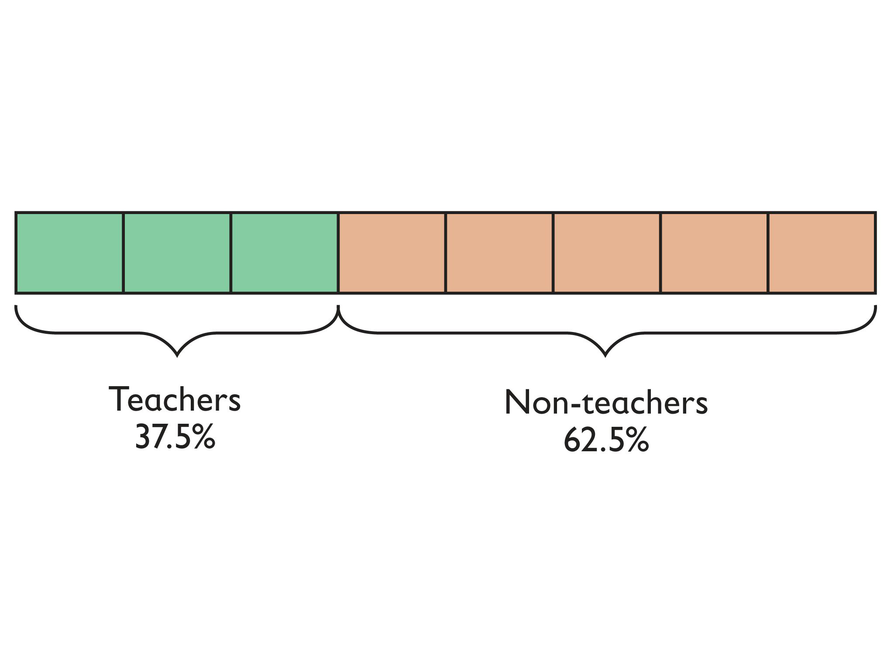
The Adults at School
Answers
- a. The ratio of teachers to adults is 3:8.
b. The ratio of non-teaching staff to adults is 5:8.
c. The ratio of non-teaching staff to teachers is 5:3.
c. 62.5% of adults are non-teaching staff.
- Diagrams will vary.
Answers will vary. Possible answer: A percent always expresses part of a whole, represented as 100%, because it gives the ratio of a number to 100. Without a whole represented as 100%, a ratio represented as a percent doesn’t have a clear meaning. A part-part ratio is implied in a percent. For example, if one part is 40%, it means the other part is 60%, and the part-part ratio is 40:60, or 2:3.
- a.
b. is the part-whole ratio of non-teaching staff to all adults at school.
c. = 0.4
0.4(1 + r) = 1
0.4 + 0.4r = 1
0.4r = 0.6
Work Time
The Adults at School
- All adults at Martin Luther King Middle School are either teachers or non-teaching staff members. The ratio of teachers to non-teaching staff is 3:5.
a. What is the ratio of teachers to adults?
b. What is the ratio of non-teaching staff to adults?
c. What is the ratio of non-teaching staff to teachers?
d. What percent of adults is non-teaching staff? Make a diagram to represent the ratio of teachers to non-teaching staff at Martin Luther King Middle School.
There are two types of ratios: part-part ratios and part-whole ratios. Explain why percents are always part-whole ratios. Refer to the tape diagram shown.
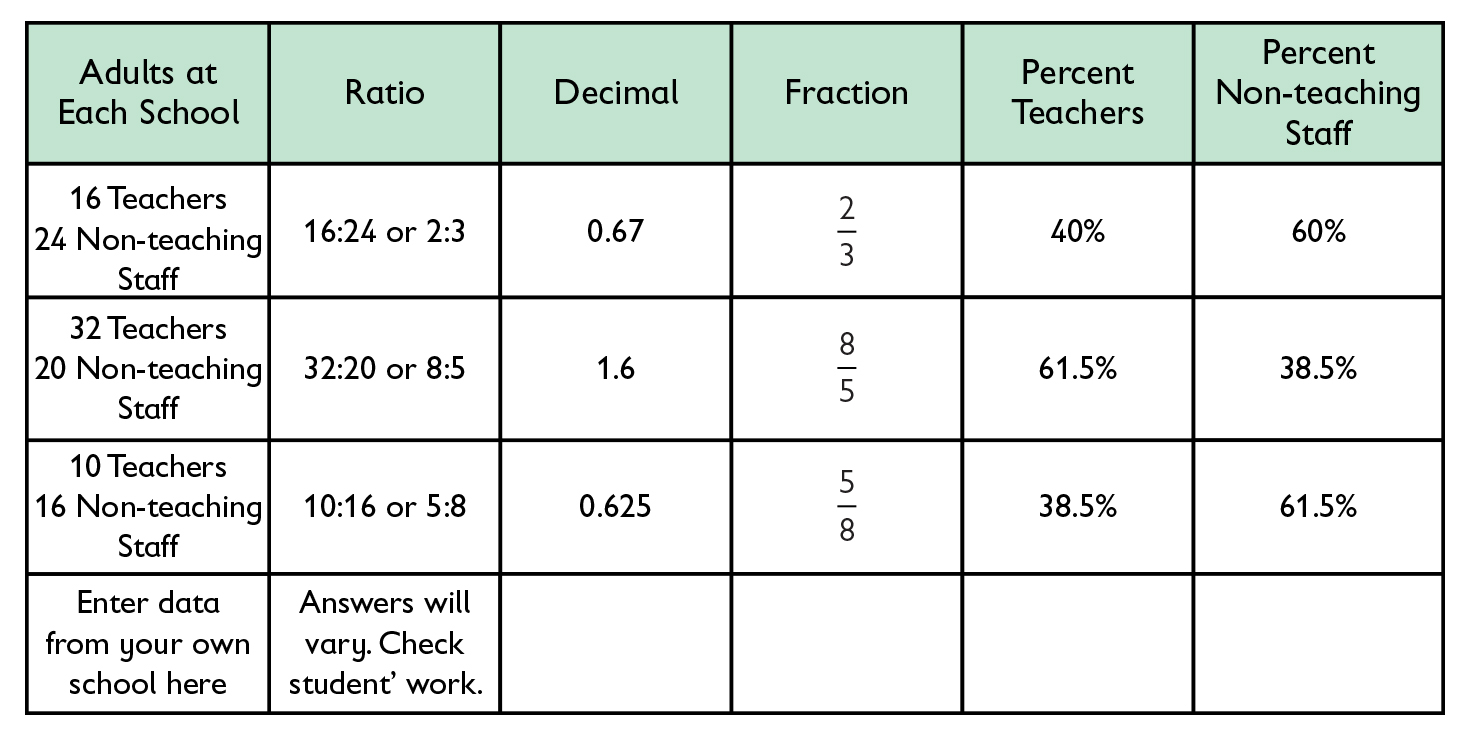
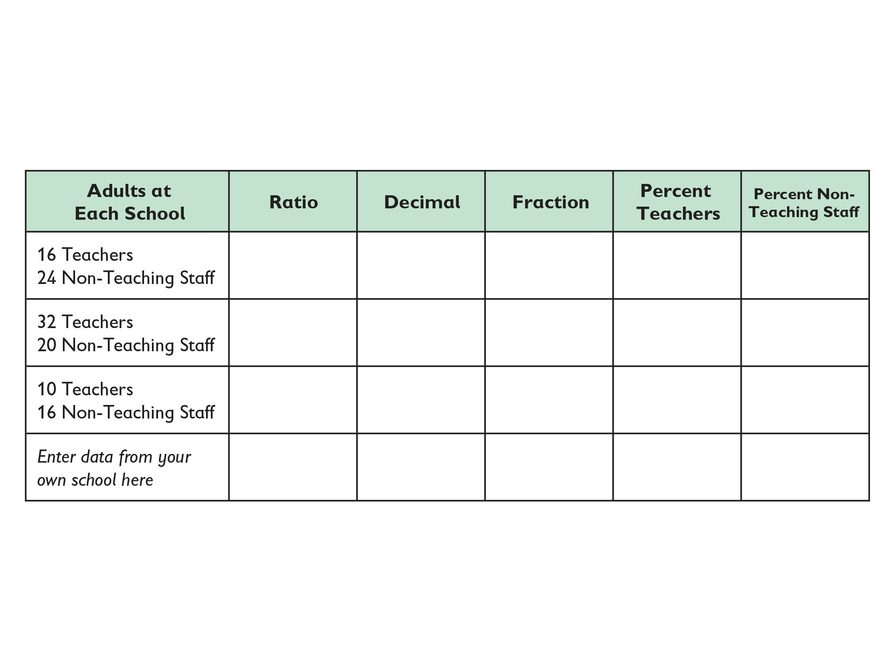
For each school listed in the table shown, give the comparison of teachers to non-teaching staff in the following forms: as a whole number ratio (a :b), as a decimal (rounded to hundredths), as a fraction in simplest form, and as a percent of the whole.
Suppose the ratio of teachers to non-teaching staff at a school is 1:r.
a. Express this ratio as a fraction.
b. What does the expression represent?
c. The teachers make up 40% of the adults at school. Calculate r.
Sports Reporters
Answers
- The second reporter is correct. The ratio of women to men (a part-part ratio) is 10:100. A ratio of women to total spectators is 10:110, which is not the same as 10% of the spectators being women. is closer to 9%.
Sports Reporters
One of the most famous soccer stadiums in the world is the Estadio Azteca in Mexico City.
The stadium can host about 111,000 spectators. During one match, there are exactly 110,000 spectators. Of the spectators, 10,000 are women.
One reporter says the ratio of women spectators to total spectators is 10:100, which is exactly 10%.
Another reporter disagrees. He says the ratio 10 women to 100 men is not the same as saying that 10% of all spectators are women.
- Misunderstandings like this happen quite often. Who is right? Explain your reasoning.
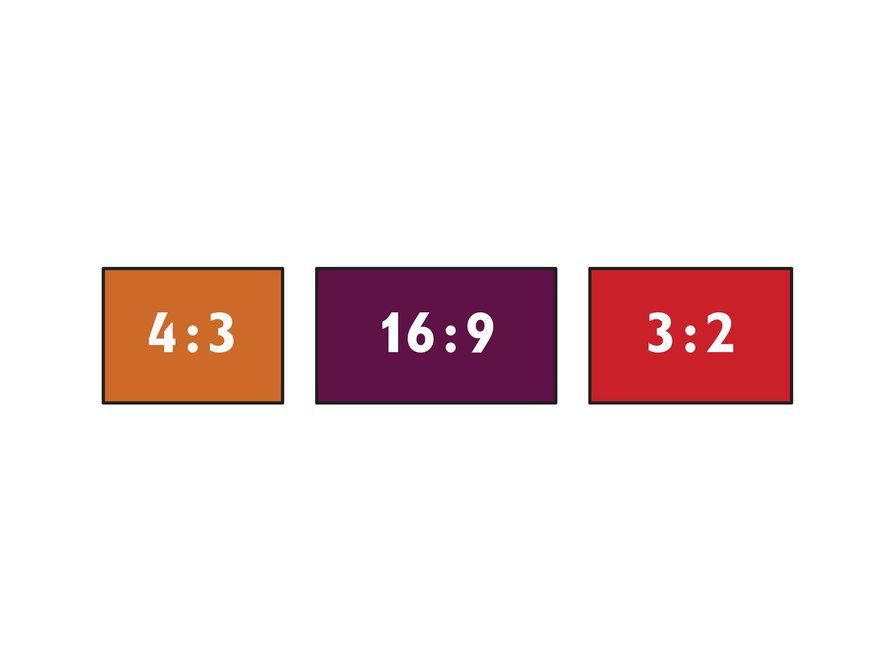
Screen Challenge
Answers
- The ratio 4:3 is most like a square.
- 1:0.75
1:0.5625
1:0.666... - The ratio 3:2 comes closest to the golden ratio.
- 4:3
- 12:5
Work Time
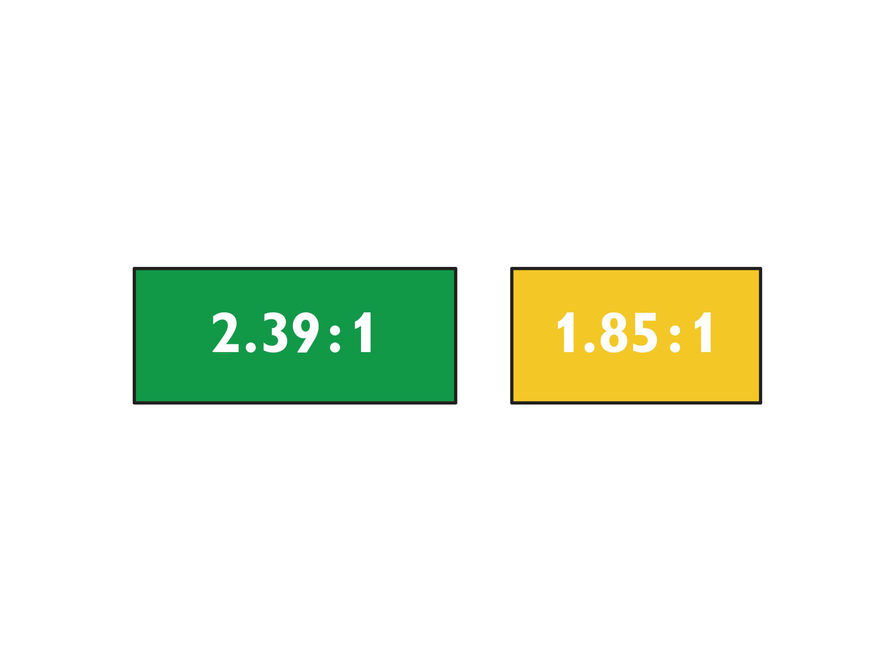
Screen Challenge
An aspect ratio compares width to height.
The following aspect ratios are used to describe the shape of different TV screens.
4:3 16 : 9 3:2
Movie screens have different formats. The two most common aspect ratios are 2.39:1 and 1.85:1.
Which TV aspect ratio gives a rectangle that is most like a square?
Write all three TV aspect ratios in the format 1 : __
The golden ratio is 1:0.6180… . This ratio is considered to create the most pleasing rectangle to the eye. Which of the three TV aspect ratios comes closest to the golden ratio?
The aspect ratio of movie screens used to be expressed in terms of the number of sprocket holes of the film. (Sprockets are the wheels that move the film.) Today, the number of pixels is used. Express the aspect ratio in lowest terms for a screen that is 640 pixels by 480 pixels (assuming square pixels).
Blu-ray discs commonly are 1,920 pixels by 800 pixels. Express this aspect ratio in lowest terms.
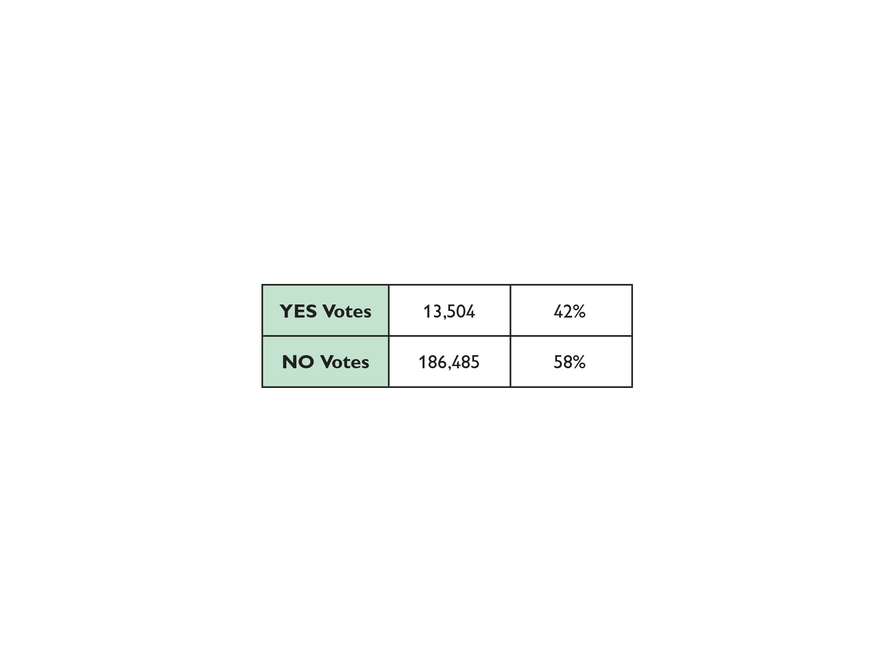
Election Results
Answers
- Answers will vary. Possible answer: The total number of votes is 199,989. The percent of Yes votes is , or about 6.8%, not 42%. The percent of No votes is , or about 93.2%, not 58%.
- Answers will vary. Possible answer: Change the number of Yes votes to 135,040. The percent of Yes votes would then be , or about 42%. The percent of No votes would be , or about 58%.
Work Time
Election Results
For a local election, the town newspaper reported the accompanying results for a bond measure.
- Explain why there must be a misprint in the table.
- Suggest a correction in one of the figures in the table that would make it consistent with the other three.
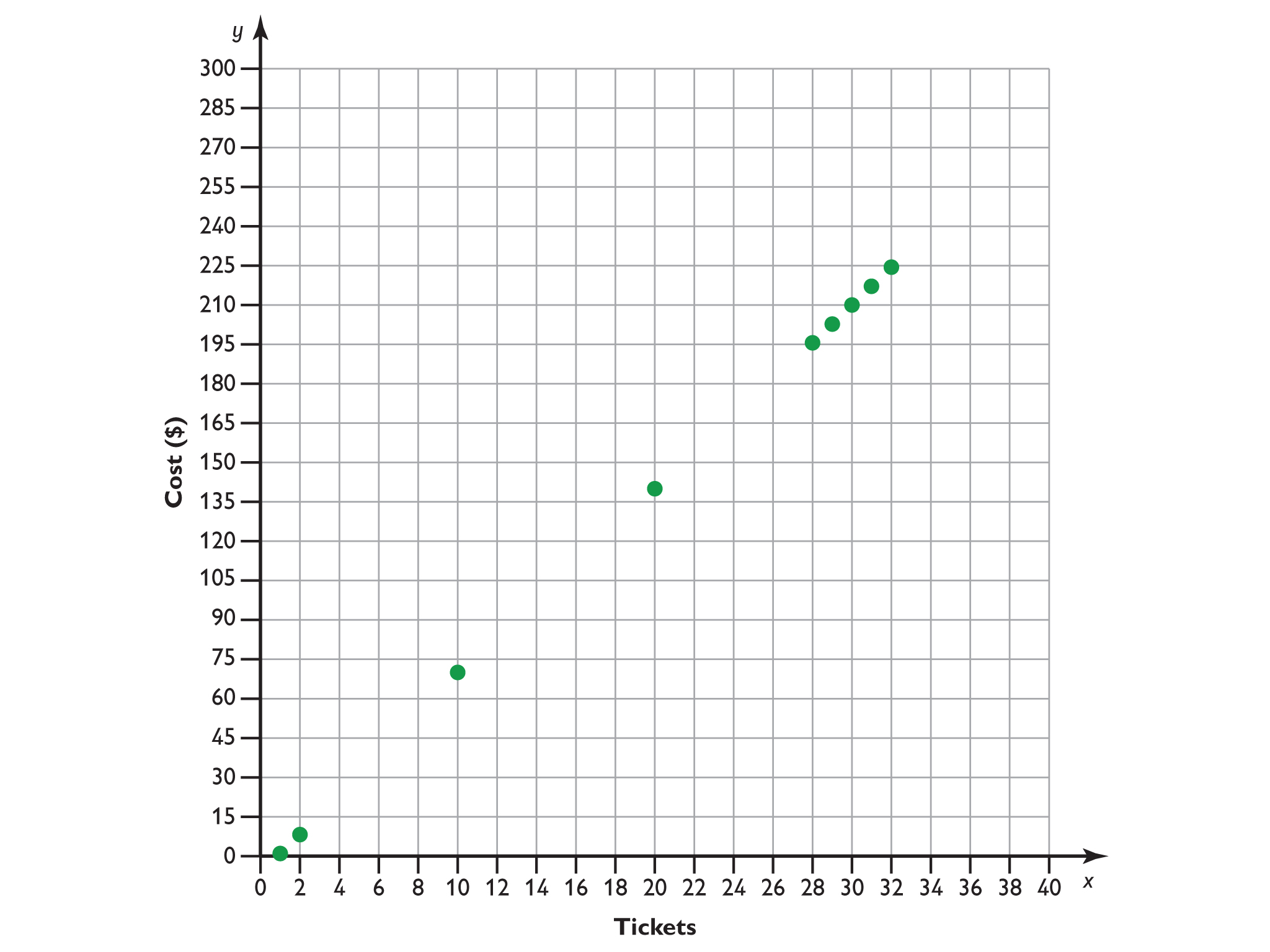
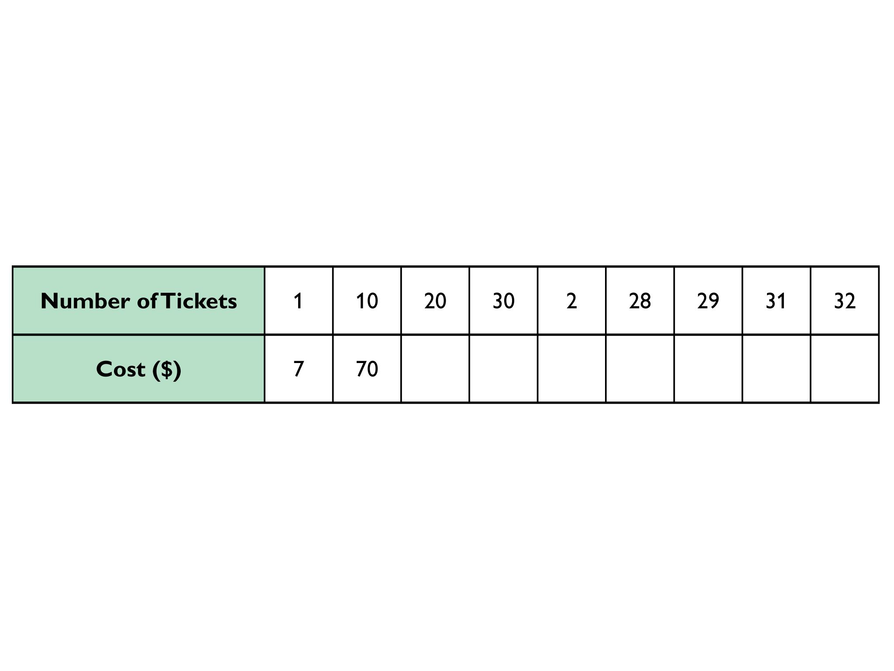
Birthday at the Movies
Answers
Explanations will vary. Some students will use the values in the first five columns to find the missing values in the last four columns as follows:
To find the cost for 28 tickets, I subtracted the cost for 2 tickets, $14, from the cost for 30 tickets, $210, to get $196.
To find the cost for 29 tickets, I subtracted the cost for 1 ticket, $7, from the cost for 30 tickets, $210, to get $203.
To find the cost for 31 tickets, I added the cost for 1 ticket, $7, to the cost for 30 tickets, $210, to get $217.
To find the cost for 32 tickets, I added the cost for 2 tickets, $14, to the cost for 30 tickets, $210, to get $224.
2.
Work Time
Birthday at the Movies
Mia’s family has invited her whole class to a movie to celebrate her birthday. Mia expects that most of the class will come. She made a ratio table to calculate the total cost for 28 to 32 students.
- Complete the table and explain your strategy.
- Make a graph to show the information in the table.
HANDOUT: Birthday at the Movies
Dinner Reservations
Answers
The restaurant needs 7 tables to seat 26 people.
Work Time
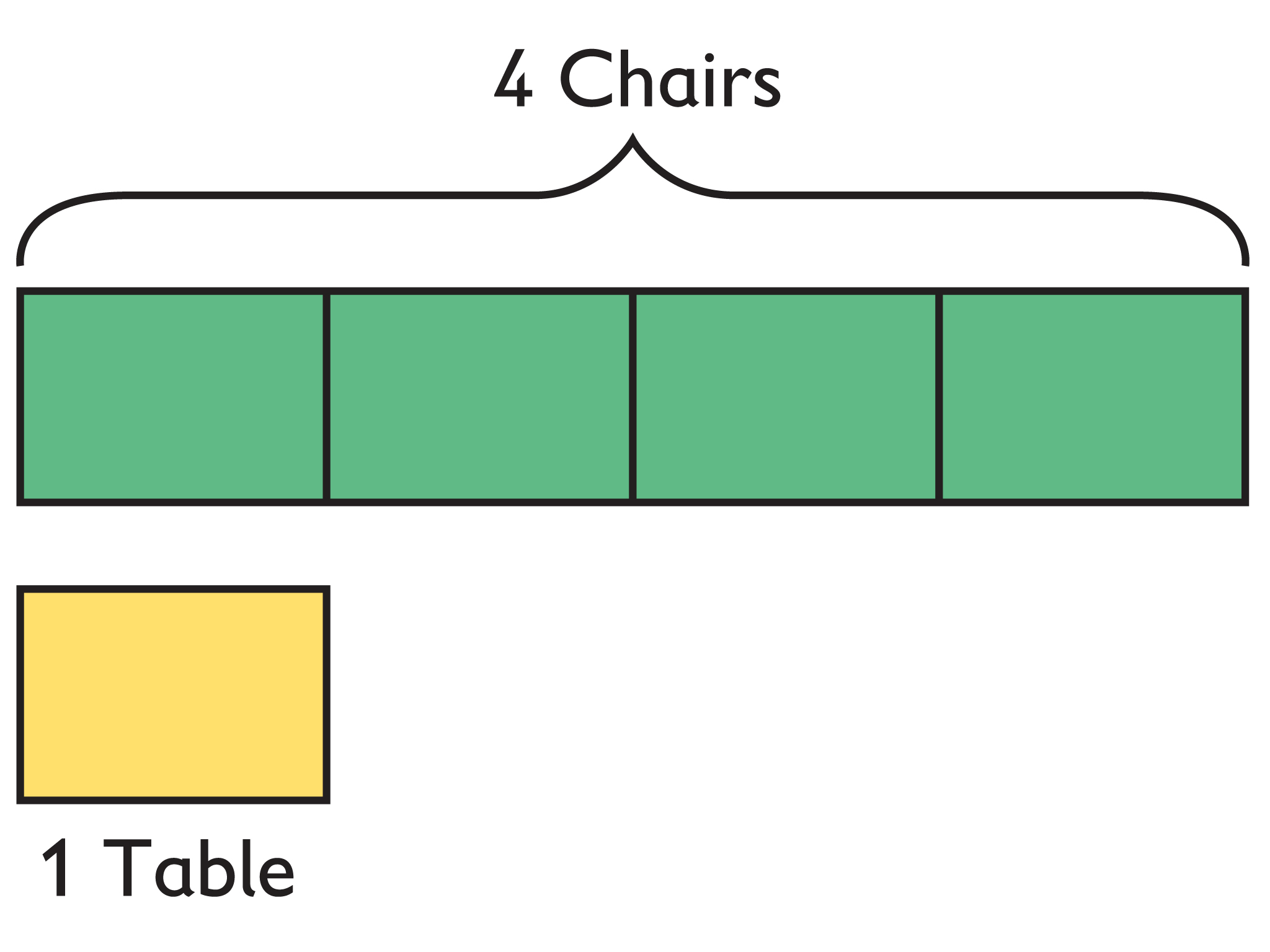
Dinner Reservations
The ratio of tables to chairs in a restaurant is 1:4.
- Sketch a tape diagram to represent this situation. Be sure to label your tape diagram accurately.
- It’s graduation night, and the restaurant has a reservation for a party of 26 people. How many tables does the restaurant need for this party? (Assume the tables are not pushed together.)
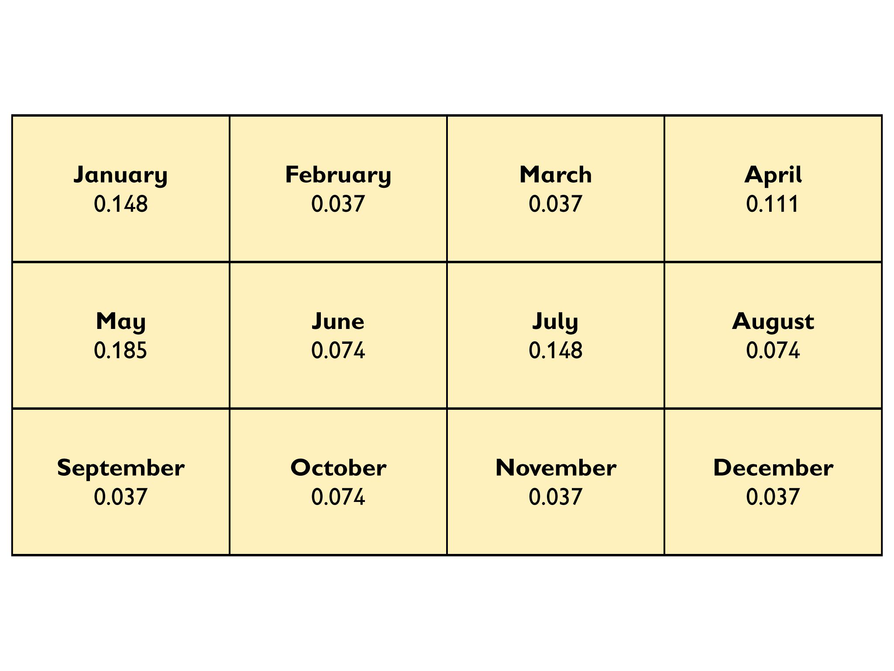
Birth Months
Answers
- 7.4% of the students were born in June.
- The ratio of the number of students born in January to the number of students born in February is 148:37, or 4:1.
- The ratio of the number of students born in January to the total number of students in the class is 148:1,000, or 37:250.
- There might be 27 students in the class. Possible explanation: If you look at the least ratio, 0.037, all other ratios are multiples of it. So, if the least ratio represents 1 student, then 0.074 represents 2 students, 0.111 represents 3 students, 0.148 represents 4 students, and 0.185 represents 5 students. Then if you add up all the students, there are 27 students in the class.
Work Time
Birth Months
The data in the table represents the ratio of students in a class who have birthdays in each month.
- What percent of the students were born in June?
- What is the ratio of the number of students born in January to the number of students born in February?
- What is the ratio of the number of students born in January to the total number of students in the class?
- Look carefully at the numbers in the table. About how many students might be in the class? How can you tell?