- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Expressing Ratios Numerically

Overview
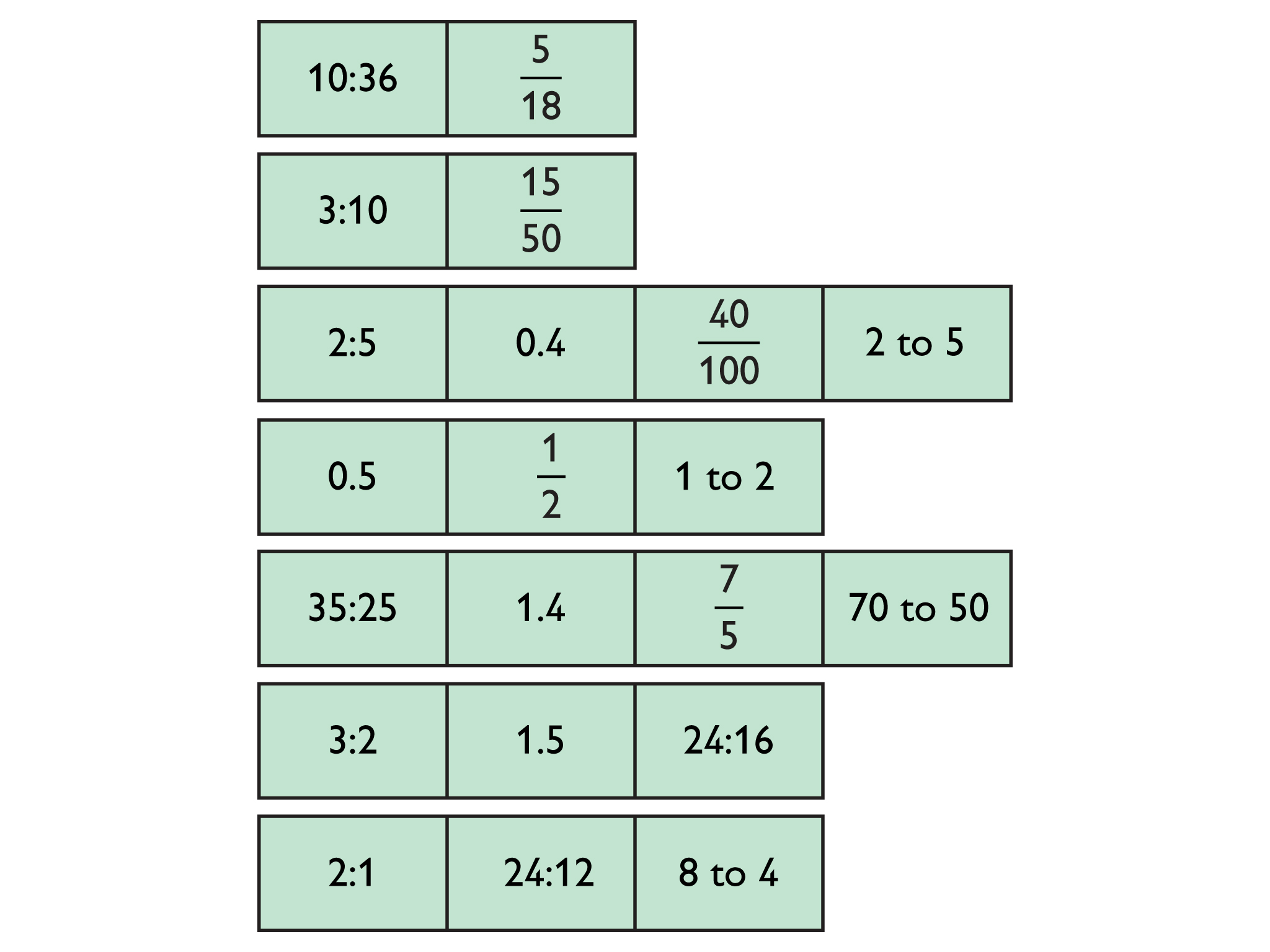
Students work with a set of cards showing different ways of expressing ratios numerically. They group the cards showing equivalent ratios and then order the groups from least to greatest value.
Key Concepts
It can be hard to compare the values of ratios represented in different forms (e.g., a:b, decimal, fraction, a to b). Simplifying ratios makes it easier to compare and order their values.
Goals and Learning Objectives
- Identify ratios that are equivalent but expressed differently.
- Simplify ratios in order to group and order cards efficiently and successfully.
Paint
Lesson Guide
Have students read Mia’s statement. Then ask partners to discuss her reasoning and answer the question: “Why is it more difficult to compare and than it is to compare and ?
ELL: Modeling is an easy and effective strategy to use when working with ELLs. Demonstrating an activity step by step allows students to focus on the task rather than the language embedded in the instructions.
Make sure students can convert a ratio in colon notation to the fraction form. Some students may find it easier to reduce and compare fractions rather than the ratio in colon notation.
Mathematics
The start of the lesson introduces the strategy of simplifying ratios as a way of comparing their values more easily.
SWD: Go over the mathematical language used throughout this lesson. Make sure students use that language when discussing the problems.
Opening
Paint
Mia used the following reasoning to determine which paint is redder:
"I think it will be difficult to compare the two ratios in the problem because the numbers are so large. Maybe if I find equivalent ratios that have smaller numbers, it will be easier to solve the problem.
"The ratio of red to yellow in the Sunset paint is . This ratio is equivalent to the ratio .
"The ratio of red to yellow in the Apple paint is . This ratio is equivalent to the ratio .
"It’s easy to compare and . I know that is greater than . So, the Sunset paint is redder than the Apple paint."
- Talk to your partner about Mia's reasoning. Why is it more difficult to compare and than it is to compare and ?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will compare ratios using the simplest form of each ratio.
Opening
Compare ratios using the simplest form of each ratio.
Find Equivalent Paint Ratios
Lesson Guide
Have students work in pairs on the card sort and the presentation.
Students take turns grouping cards that represent the same ratio and explain to their partner how they know the cards go together; each partner either agrees or challenges the explanation if it is not clear and complete.
When all cards have been grouped, partners sort the sets of cards in order from least to greatest value.
SWD: Use card sorting activities to encourage students to experiment—they can move the cards around if they change their minds. This type of activity encourages discussion, because students have to explain to each other why they think certain cards match.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Listen for the ways students respond to each other’s reasoning and work together to develop clearer and more complete explanations for their grouping choices.
Mathematical Practice 6: Attend to precision.
Listen for students using a range of vocabulary in discussing the equivalence of the cards in each group. For example, they may talk about the cards having “equal value” or just being “equal,” or they may use the term equivalent. (All of these are correct.) On the other hand, they may talk about them as “the same” or use other less precise language.
Interventions
Student has difficulty getting started.
- Do you see any cards that show the same value but are expressed in different forms?
Student matches cards in pairs rather than in groups.
- Describe the task in your own words to your partner.
- What about these cards? Do they show the same values as these? If so, they should be in the same group.
Student has trouble ordering cards from least to greatest value.
- Try simplifying the ratios and fractions and then comparing them.
Answers
Work Time
Find Equivalent Paint Ratios
Work with a partner.
- Take turns finding and grouping cards that represent the same ratio of red paint to yellow paint.
- Explain to your partner how you know that the cards represent the same ratio.
- Your partner should either agree with your explanation or challenge it if your explanation is not correct, clear, or complete.
- When you have finished grouping all the cards in a way that you both agree on, arrange the sets of cards in order from least to greatest (the least red to the most red).
INTERACTIVE: Card Sort
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student strategies for comparing fractions:
- Students who use basic number sense, for example, is less than so the value of the ratio 5:18 is less than the value of the ratio 1:2
- Students who find common denominators
- Students who convert to decimals in order to compare the values
Students who use cross products (If students are using this method, make sure they understand what they are doing and are not just doing a rote procedure.) Compare and .
Challenge Problem
Answer
- The painter needs to add 45 fluid ounces of red, 135 fluid ounces of yellow, and 90 fluid ounces of brown to the sample mixture to get a total of 360 fluid ounces of paint.
Work Time
Prepare a Presentation
You arranged your sets of paint ratio cards from least to greatest in Task 3.
- Show how you grouped the cards and how you put the sets in order.
- Include an explanation of the method(s) you used.
Challenge Problem
A painter mixes 15-fluid-ounce samples of red, yellow, and brown paint in the ratio of 1 to 3 to 2 in order to check that the resulting color is right for his mural. This sample mixture contains 90 fluid ounces (6 × 15 fluid ounces).
- For the mural, the painter needs 360 fluid ounces of paint in the same ratio (1:3:2). How many more fluid ounces of each color does he need?
Ask yourself:
How could you put the ratios on the cards in the same format to make them easier to compare?
Make Connections
Mathematics
Have students share a range of strategies for identifying equivalent values, including at least one student presentation for each type of number. Call attention to students’ strategies that involve finding the simplified form of each ratio (this may be every strategy presented); ask students why simplifying ratios is a good strategy.
ELL: Be cognizant that ELLs may encounter difficulties when they have to express themselves in a foreign language. If you hear that they say the right things but use the wrong grammar structure, show signs of agreement and softly rephrase using the correct grammar. Use the student’s words as much as possible.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Ask at least one student pair to describe a disagreement they had and how they resolved it; be sure that the pair has an opportunity to present a clear and coherent argument that justifies their resolution about where to place the card in dispute. If their argument could use refinement, ask the class to help add to or revise the argument as needed.
Mathematical Practice 6: Attend to precision.
As students present their work, and in particular, as the resolution of a disagreement is presented and discussed, call attention to the language students are using, with a focus on the mathematically correct usage of the terms equivalent and ratio.
Performance Task
Ways of Thinking: Make Connections
Take notes as your classmates present their methods for putting the ratio cards into sets of equal ratios and ordering the sets.
As your classmates present, ask questions such as:
- Did you and your partner have any disagreements about which cards represent the same ratio? If so, how did you resolve your disagreement?
- Do you think simplifying ratios that are represented as fractions is a good strategy? Why or why not?
- What do you think is the easiest way to tell whether two ratios are equivalent?
- Did you rewrite any of the ratios to help you determine how to arrange them from least to greatest? If so, how did you rewrite the ratios?
Ratios in Simplest Form
A Possible Summary
When comparing two ratios, it is sometimes easier to tell which has a greater value if you simplify the ratios first. This is an especially good strategy if you have to put many ratios in order from greatest to least value.
Additional Discussion Points
Here are some additional points you may wish to discuss:
- An explantion about why it is often easiest to work with the simplest form of a ratio
- A description of how to find the simplest form of a ratio
- A description of how to order a set of ratios by their values
Formative Assessment
Summary of the Math: Ratios in Simplest Form
Write a summary about using the simplest form of ratios and comparing ratios.
Check your summary.
- Do you discuss why it is often easier to work with the simplest form of a ratio?
- Do you explain how to find the simplest form of a ratio?
- Do you describe how to compare and order ratios?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students know about the relationship between ratios and fractions.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One way that I could figure out the relationship between the ratio 3:2 and the fraction is to …