- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Double Number Line Tool
Mathematical Practice 5
Ratio Table Tool
Glide Ratio

Overview
This lesson introduces the concept of a glide ratio and encourages students to use appropriate tools strategically (Mathematical Practice 5). Students use tape diagrams, double number lines, ratio tables, graphs, and equations to represent glide ratios.
Key Concepts
A glide ratio for an object or an organism in flight is the ratio of forward distance to vertical distance (in the absence of power and wind). For a given object or organism that glides, this ratio has a constant value and is treated as a feature of the object or organism.
Goals and Learning Objectives
- Understand the concept of a glide ratio.
- Make connections within and between different ways of representing ratios.
Use Appropriate Tools
Mathematical Practices in Action
Mathematical Practice 5: Use appropriate tools strategically.
Ask the following:
- How can you represent the glide ratio of a person in a wing suit?
Have students watch the video and listen to the dialogue between Jan, Carlos, and Mia. This video shows students engaged in Mathematical Practice 5: Use appropriate tools strategically. Have students evaluate Jan's summary of which tools she would use when.
Have students brainstorm the kinds of tools that they use in mathematics. Their list might include such things as graphs and rulers. Even pencil and paper is a tool!
SWD: This lesson includes information that is presented in videos and using charting tools and images. Make sure students have the ability to customize the display of this information (this may entail simplifying the amount and/or type of information presented at one time, zooming out, zooming in, adjusting brightness and volume, and utilizing the closed caption feature).
ELL: When showing the video, monitor that the ELLs are following the meaning of what is presented. If necessary, pause the video and allow them to ask clarifying questions. Alternatively, ask questions to check for understanding about what they are watching.
Opening
Use Appropriate Tools
Today you will explore and compare glide ratios of things that fly.
In this unit, you have used tape diagrams, double number lines, ratio tables, and graphs to represent ratios, make comparisons, and solve ratio problems.
Whenever you work with ratios, you should think about the tools that are available to you and choose the one(s) that you think will be the most useful.
- How do you think your work in previous lessons might help you represent and compare ratios?
- Watch this video as Jan, Carlos, and Mia use appropriate tools to explore wingspan and glide ratios.
VIDEO: Mathematical Practice 5
Math Mission
Lesson Guide
Discuss the Math Mission. Students will solve problems about glide ratios using appropriate tools.
Opening
Solve problems about glide ratios using appropriate tools.
White-Backed Vultures
Lesson Guide
Have students work in pairs on the problem.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
Students may refer back to the representations presented in the Opening video (or from prior lessons) and think or talk about which representation to use based on what it shows, how easy it is to use in comparing different glide ratios, and what information it yields compared to other representations.
Mathematical Practice 4: Model with mathematics.
Listen for students who recognize that they are using different representations to model the effects (distances and heights) of the different glide ratios of physical living and nonliving things.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students may also engage in productive discussion and debate in their pairs about the value of different representations in the context of today’s problems.
Interventions
Student switches the position of forward distance and vertical distance or doesn't think it matters.
- How can you tell which comes first (or goes on top), the forward distance or the vertical distance?
- Look back at the definition of glide ratio given in the video, and check that your representation fits the way it is defined.
- Which should always have a greater value for the glide ratio, the forward distance or the vertical distance?
- In each case, the thing that glides is moving forward more quickly than it is moving down. Check that your representation of the glide ratio reflects this fact.
Student has trouble understanding the double number line tool.
- What does the double number line show?
- Select two points on a double number line. What do those points represent?
Student has trouble understanding the ratio table tool.
- Choose a pair of values from the table. What do the pair of values mean?
- Could you continue adding pairs of values to the table?
Possible Answers
- Models will vary.
- For every 1 foot the white-backed vulture descends, it glides forward 15 feet.
Work Time
White-Backed Vultures
White-backed vultures have a glide ratio of 75:5. The ratio tells us that this kind of vulture can glide 75 feet forward for every 5 feet that it descends.
Choose a tool that you think will be useful for representing and comparing equivalent glide ratios for the white-backed vulture. (The Double Number Line Tool and Ratio Table Tool are provided below; however, you can use any tool that you feel will be the most useful.)
- Using your chosen tool, represent equivalent glide ratios for the white-backed vulture.
- Explain where you "see" the ratios in your representation and what each ratio means.
INTERACTIVE: Double Number Line Tool
INTERACTIVE: Ratio Table Tool
When representing and comparing the glide ratios, pay attention to which numbers you use for the forward distances and which you use for the vertical descent distances.
Paragliders and Sailplanes
Lesson Guide
Have students work in pairs on the problem. Students should use the same tool they used for the white-backed vulture problem.
Mathematical Practices
Mathematical Practice 5: Use appropriate tools strategically.
Students may refer back to the representations presented in the Opening video (or from prior lessons) and think or talk about which representation to use based on what it shows, how easy it is to use in comparing different glide ratios, and what information it yields compared to other representations.
Mathematical Practice 4: Model with mathematics.
Listen for students who recognize that they are using different representations to model the effects (distances and heights) of the different glide ratios of physical living and nonliving things.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students may also engage in productive discussion and debate in their pairs about the value of different representations in the context of today’s problems.
Interventions
Student has trouble understanding the double number line tool.
- What does the double number line show?
- Select two points on a double number line. What do those points represent?
Student has trouble understanding the ratio table tool.
- Choose a pair of values from the table. What does the pair of values mean?
- Could you continue adding pairs of values to the table?
Possible Answers
- Models will vary.
- For every 1 foot the sailplane descends, it glides forward 50 feet.For every 1 foot the paraglider descends, it glides forward 6 feet.
Work Time
Paragliders and Sailplanes
Sailplanes have a glide ratio of 150:3.
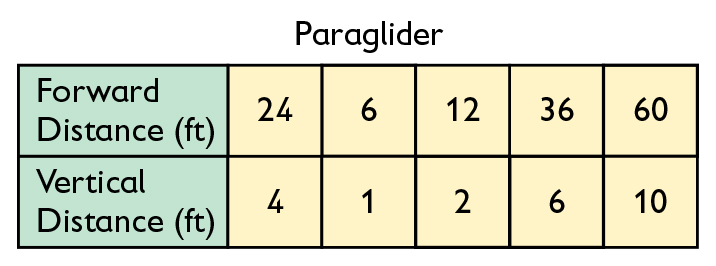
Paragliders have a glide ratio of 24:4.
- Choose either the sailplane or the paraglider. Use the same tool you used with the white-backed vulture to represent equivalent glide ratios for the sailplane or the paraglider.
- Explain the meaning of each of the ratios.
INTERACTIVE: Double Number Line Tool
INTERACTIVE: Ratio Table Tool
Hint:
When representing the glide ratios, pay attention to which numbers you use for the forward distances and which you use for the vertical descent distances.
Compare Glide Ratios
Lesson Guide
Have students work in pairs on the problem.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Listen for students who recognize that they are using different representations to model the effects (distances and heights) of the different glide ratios of physical living and nonliving things.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students may also engage in productive discussion and debate in their pairs about the value of different representations in the context of today’s problems.
Possible Answers
Answers will vary. Possible answer:
From the altitude of 10 feet, the sailplane travels 500 feet horizontally.
From the altitude of 10 feet, the white-backed vulture travels 150 fet horizontally.
The sailplane can glide farther than the white-backed vulture from a given altitude.
The sailplane glides at a ratio of 50:1, while the white-backed vulture glides at a ratio of 15:1.
Work Time
Compare Glide Ratios
Based on their glide ratios, which of these can glide farther from a given altitude:
- The white-backed vulture or the sailplane or the paraglider?
- Explain and support your answer using the representations you made.
When representing and comparing the glide ratios, pay attention to which numbers you use for the forward distances and which you use for the vertical descent distances.
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student thinking to highlight during the Ways of Thinking discussion:
- Students who discuss and rethink which representation to use
- Students who make efficient and effective use of ratio tables
- Students who make efficient and effective use of double number lines
- Students who make efficient and effective use of equations
- Students who make connections across representations of glide ratios
Challenge Problem
Answers
- Possible representation:
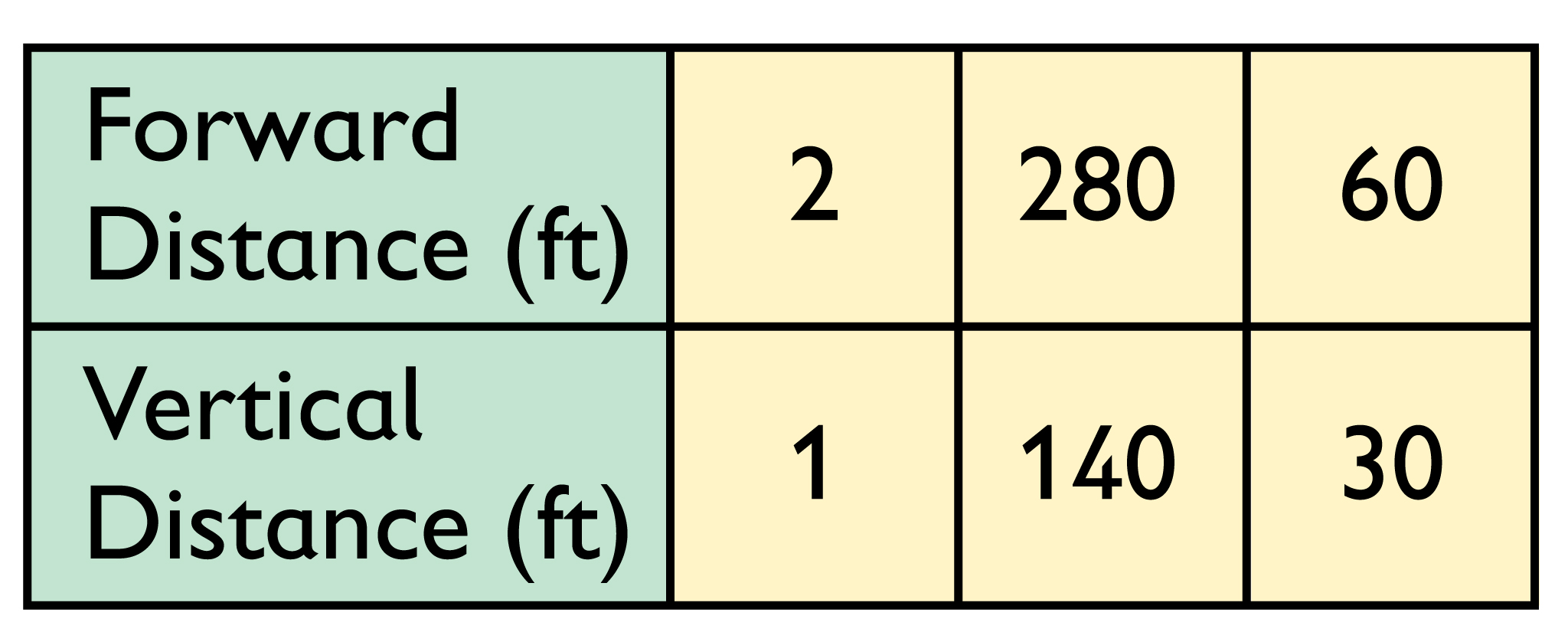
280 − 60 = 220
The two trees are 220 feet apart.
- The squirrel jumped from a branch that was 70 feet high.
20 + 120 = 140
140 ÷ 2 = 70
Or, the horizontal distance was 120 feet, so the vertical change was 60 feet.
60 +10 = 70
Work Time
Prepare a Presentation
Explain what a glide ratio is.
Explain which tool you chose to represent glide ratios and why you chose that tool.
Explain how the representations you made support your answer about whether the vulture or the sailplane/paraglider can glide farther from a given altitude.
Challenge Problem
As you can see in the photograph, the northern flying squirrel has its own wing suit! This wing suit is similar to a wing suit that humans have developed. The squirrel has a glide ratio similar to the glide ratio of the man-made wing suit: both ratios are approximately 2:1.
- Imagine that the squirrel jumps from one tree to another, from a branch 140 feet off the ground to a branch 30 feet off the ground. How far apart are the two trees?
- Another set of trees is 120 feet apart. The squirrel jumps from one tree branch to another and lands on a branch that is 10 feet off the ground. How high was the branch that the squirrel jumped from?
Make Connections
Mathematics
Use the Ways of Thinking discussion to help students make connections across representations. As students present their work, ask students how the ratio between forward and vertical distance is visible in each representation. Ask students which tool for representing ratios they prefer in this context and why. Once you have at least three different representations for the class to see, make the mathematically relevant connections and distinctions between them more explicit by asking students to identify correspondences between them and to explain what can and cannot be shown by each.
Conclude the discussion by focusing on the kinds of questions you can answer using each representation. For example, ask:
- What tool(s) would you use if you wanted to know how far someone in a wing suit would get before they reached the ground after jumping from a given height, gliding in a single direction?
- What tool(s) would you use if you wanted to compare the glide ratio of two different models of sail planes?
- What other questions might someone be interested in about glide ratios, and what tool(s) would work best to answer them?
SWD: Some students with disabilities may struggle to explain their mathematical reasoning in words. Provide sentence starters to assist students in their explanations for which tool(s) they preferred and why.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' representations and the strategies they used for comparing glide ratios.
As your classmates present, ask questions such as:
- Which tool do you think is the most useful for comparing glide ratios? Why?
- Which tool would be the most useful for determining the distance a bird can travel before reaching the ground if you only know its starting height and glide ratio?
- Which tool did you work from to make your graph?
Represent and Compare Glide Ratios
A Possible Summary
There are many tools for representing ratios, including tape diagrams, tables, double number lines, equations, and graphs. Tape diagrams show one ratio at a time, whereas tables and double number lines show sets of equivalent ratios. The slope of a graph shows the ratio, and the points on the graph give values that are equivalent ratios. The equation of the graph can also be used to find equivalent ratio values. A glide ratio is the ratio of forward distance to vertical distance. Tools that show many equivalent ratios are more useful for comparing glide ratios and for making predictions based on glide ratios.
Additional Discussion Points
Here are additional points to discuss:
- The definition of glide ratio
- A description of different ways to represent ratios
Formative Assessment
Summary of the Math: Represent and Compare Glide Ratios
Write a summary about representing and comparing glide ratios and the tools that help you do this.
Check your summary.
- Do you define glide ratio ?
- Do you describe different ways to represent ratios?
- Do you describe the different tools you can use to represent glide ratios?
- Do you explain how you can use these representations to compare glide ratios?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what glide ratio students would like if they could fly.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
If I could fly, I would like my glide ratio to be ____ because …