- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Double Number Lines

Overview
Students use double number lines to model relationships and to solve ratio problems.
Key Concepts
Double number line diagrams are useful for visualizing ratio relationships between two quantities. They are best used when the quantities have different units. (The unit rate appears paired with 1.) Double number line diagrams help students more easily “see” that there are many equivalent forms of the same ratio.
Goals and Learning Objectives
- Understand double number line diagrams as a way to visually compare two quantities.
- Use double number line diagrams to solve ratio problems.
Introduction to Double Number Lines
Lesson Guide
Review the problem and how the double number line diagram represents possible photograph sizes. Answer the questions as a class.
Answers will vary. Possible answer: 7.5 and 10.5
Each lined-up pair of numbers represents an enlarged 5-inch-by-7-inch photograph size.
ELL: Point to or highlight the parts of the double number line that you are referring to so that students can follow along.
Mathematics
Discuss how to set up a double number line to represent the ratio 5:7. Be sure students understand why the 5 and 7 are lined up on both number lines and how to add other number pairs to the number line diagram. Highlight the multiplicative nature of ratios.
SWD: Remind students that a double number line is a tool that can be applied to many different mathematical situations. For example, we just used the number line to “see” multiples of 5 and 7. Ask students to tell you how using this double number line differs from other number lines they have used.
Opening
Introduction to Double Number Lines
Read and Discuss
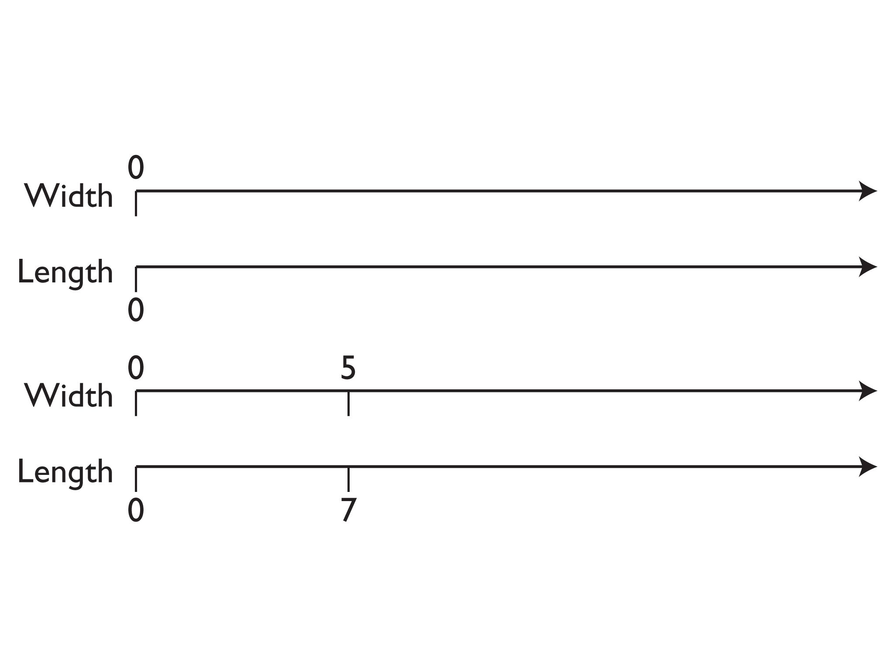
A company will enlarge 5-inch-by-7-inch photographs to any size you want.
You can use a double number line to help you see some of the possible photograph sizes.
- To make a double number line, you start with two number lines and line them up at 0.
- You know that the ratio of the width of the original photograph to its length is 5:7, so you would make one tick mark on the top line at 5 and another tick mark on the second line at 7, making sure that the 5 and 7 are lined up.
- Now you can add other numbers to the number lines.
- What are some of the possible photograph sizes you can order?
- What is another pair of numbers that would line up on this double number line?
- What does each lined-up pair of numbers represent? (Think of the question from the problem.)
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use double number line diagrams to solve ratio problems.
Opening
Use double number lines to solve ratio problems.
Baseball Fields
Lesson Guide
Have students work in pairs on the problems and the presentation.
SWD: Some students may need direct instruction to make connections between previously learned concepts and newly introduced mathematical ideas. Assist struggling students in using what they know about multiples to find their solutions for the double number line.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students represent ratios as double number line diagrams in order to represent and solve problems.
Mathematical Practice 6: Attend to precision.
Students may struggle with how best to communicate how to set up the double number line diagram; prepare to build on these efforts in the Ways of Thinking discussion, with attention to the clarity and precision of explanations.
Interventions
Student has difficulty getting started.
- Explain the problem to your partner.
- What will the top number line represent? What will the bottom number line represent?
- Look back at the double number line diagrams from the start of the lesson. How is the ratio 5:7 shown?
- How can you show the ratio 2:3 on a double number line?
- How can you add other number pairs to the double number line?
The student makes a double number line diagram that doesn’t represent the baseball fields.
- Explain what your double number line diagram shows to your partner.
- Where is the value “2” shown in your double number line diagram? Where is the value “3” shown in your double number line diagram?
- How many times as far is 20 from 2? What number is that many times as far from 3?
Answers
- The distance from home plate to first base on a major league field is 30 yards.
- The distance from home plate to the left field fence on a high school field is 80 yards.
Work Time
Baseball Fields
Each of the measurements of a high school's softball field is in a 2:3 ratio to the corresponding measurements of the state’s major league baseball team field.
- Using the double number line tool, make a double number line that represents this ratio. Then use your double number line to answer the following questions.
- The distance from home plate to first base on the high school field is 20 yards. What is the distance in yards from home plate to first base on the major league field?
- The distance from home plate to the left field fence on the major league field is 120 yards. What is the distance in yards from home plate to the left field fence on the high school field?
INTERACTIVE: Double Number Line Tool
- What does each lined-up pair of numbers on your double number line represent?
- Where do you see 20 yards on the line representing the high school field?
- Where do you see 120 yards on the line representing the major league field?
Recipes
Lesson Guide
Have students work in pairs on the problems and the presentation.
ELL: When forming pairs, be aware of your ELLs and ensure that they have a productive learning environment. Different types of partnerships include:
- Pairing them up with English speakers so they can learn language skills.
- Pairing them up with students who are at the same level of language skills so they can take a more active role and they can work things out together.
- Pairing them up with students whose proficiency level is lower so they play the role of the "supporter."
You can also pair them up based on their math proficiency.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Students represent ratios as double number line diagrams in order to represent and solve problems.
Mathematical Practice 6: Attend to precision.
Students may struggle with how best to communicate how to set up the double number line diagram; prepare to build on these efforts in the Ways of Thinking discussion, with attention to the clarity and precision of explanations.
Interventions
Student has difficulty getting started.
- Explain the problem to your partner.
- What will the top number line represent? What will the bottom number line represent?
- Look back at the double number line diagrams from the start of the lesson. How is the ratio 5:7 shown?
- How can you show the ratio on a double number line?
- How can you add other number pairs to the double number line?
Student makes a double number line diagram that doesn’t represent the recipe situation.
- Explain what your double number line diagram shows to your partner.
- Where is the value “6” shown in your double number line diagram? Where is the value “2” shown in your double number line diagram?
Answers
- You would need 3 tablespoons of salad oil for 1 tablespoon of vinegar.
- You would need 5 tablespoons of vinegar for 15 tablespoons of salad oil.
Work Time
Recipes
Ratios are important in cooking. No matter what amount you make, you need to use the right ratio of ingredients in a recipe for the dish to taste the same every time.
Suppose that the recipe for an oil-and-vinegar dressing requires 6 tablespoons of salad oil and 2 tablespoons of vinegar.
- Create a double number line that shows this relationship. Use the Double Number Line Tool if you find it to be helpful.
- Use your double number line to determine how many tablespoons of salad oil you would need if you had 1 tablespoon of vinegar.
- How many tablespoons of vinegar would you need if you had 15 tablespoons of salad oil?
INTERACTIVE: Double Number Line Tool
What number on the line representing the vinegar should you line up with the 6 on the line representing the salad oil?
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student thinking to highlight during the Ways of Thinking discussion:
- Students who debate about how to set up the double number line diagram
- Students who used different strategies to solve the problem using a double number line diagram
- Students who have difficulty modeling the problem situation with a double number line
Challenge Problem
Answers
- The double number line would represent a ratio of 1:3 instead of 2:3. All the high school field dimensions would be halved to represent the little league field dimensions.
- The ratio between the little league field dimensions and the high school field dimensions would be 1:2.
Work Time
Prepare a Presentation
Provide your solutions to each question. Write your solutions using complete sentences.
Explain how you used double number lines to solve each of the problems.
Compare the way you used the double number lines with the way you could use a tape diagram to solve these problems.
Challenge Problem
In the problem about the baseball fields, the ratio of the high school field dimensions to the major league field dimensions is 2:3.
Suppose a local little league team wants to build a baseball field with measurements in a 1:3 ratio to those of the major league field.
- How would your double number line change?
- What would the ratio be between the little league field and the high school field?
Make Connections
Mathematics
Have presenters explain how they created and used the double number line diagrams to solve the problems. Ask:
- What does the top number line represent? What does the bottom number line represent?
- Where do you see the ratio on your double number line diagram?
- How did you figure out what other number pairs to line up on your double number line diagram?
- How did you use your double number line to solve the problem?
- How do you know your answer is reasonable?
- Can you make a tape diagram to solve this problem? What would it look like?
- How is the tape diagram similar to and different from the double number line diagram?
Be sure to discuss that a tape diagram compares two quantities by representing each quantity as a length, with both lengths divided into units of equal length. A double number line shows each of the quantities on its own number line, with corresponding pairs of values lined up; the units on each number line are not the same unless there is a 1:1 ratio between the quantities.
Have students who completed the Challenge Problem present their solution and discuss as a class.
ELL: When critiquing students whose proficiency in English is low, focus on what the student is trying to convey and not the grammar mistakes. If you are not sure you understand, ask the student to repeat in different ways. If other students in the class understand (and you don’t), allow them to help you.
Performance Task
Ways of Thinking: Make Connections
Take notes about how your classmates used the double number line to solve the problems and how they compared the double number line to the tape diagram.
As your classmates present, ask questions such as:
- Can you explain the meaning of the pairs of numbers that line up on the double number line?
- How did you make the double number line for the salad dressing recipe?
- Do you think it’s easier to use a double number line or a tape diagram to solve ratio problems?
Different Ways to Represent Ratios
Mathematics
Have pairs quietly discuss how both tape diagrams and double number line diagrams represent ratios. As student pairs work together, listen for students who may still have misconceptions so you can address them in the class discussion. After a few minutes, discuss the Summary as a class. Have volunteers explain how tape diagrams and number line diagrams can be used to represent ratios and to solve ratio problems.
Formative Assessment
Summary of the Math: Different Ways to Represent Ratios
Read and Discuss
- You can use both tape diagrams and double number lines to show ratios.
- This tape diagram shows that the ratio of pints of red paint to pints of blue paint in a paint mixture is 4:7.
- Thus, one way to produce a mixture with the correct ratio is to mix 4 pints of red paint with 7 pints of blue paint.
- You can use a double number line if you want to show many different ways to mix the paint and still get the same ratio of red to blue (and thus the same final paint color).
- This double number line shows that you can mix 4 pints of red paint with 7 pints of blue paint, or 8 pints of red paint with 14 pints of blue paint, or 12 pints of red paint with 21 pints of blue paint, and so on.
- You will still get a paint mixture that has a 4:7 ratio of red paint to blue paint.
Can you:
- Explain how to use tape diagrams to represent ratios?
- Explain how to use double number lines to represent ratios?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out how students think a tape diagram is similar to or different from a double number line.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starters below if you find them to be helpful.
I think a tape diagram is similar to a double number line because …
I think a tape diagram is different from a double number line because …
Can you:
- Explain how to use tape diagrams to represent ratios?
- Explain how to use double number lines to represent ratios?