- Author:
- Chris Adcock
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Percent Statements about Data

Overview
Students interpret multiple categories of data about a hypothetical village population that represents the global population. They determine whether percent statements about the data are true or false.
Key Concepts
Data presented in multiple formats can be investigated using percent statements that facilitate comparisons between different parts of a whole. In using percents to interpret data, it is essential to be clear about what the part is and what the whole is. The whole in this lesson is a representative sample of the global population, which is used as a model for investigating variation across the population.
Goals and Learning Objectives
- Interpret data presented in different formats in terms of percents.
- Identify percent statements as true or false, if possible, and explain the decision.
- Modify false percents statements to make them true.
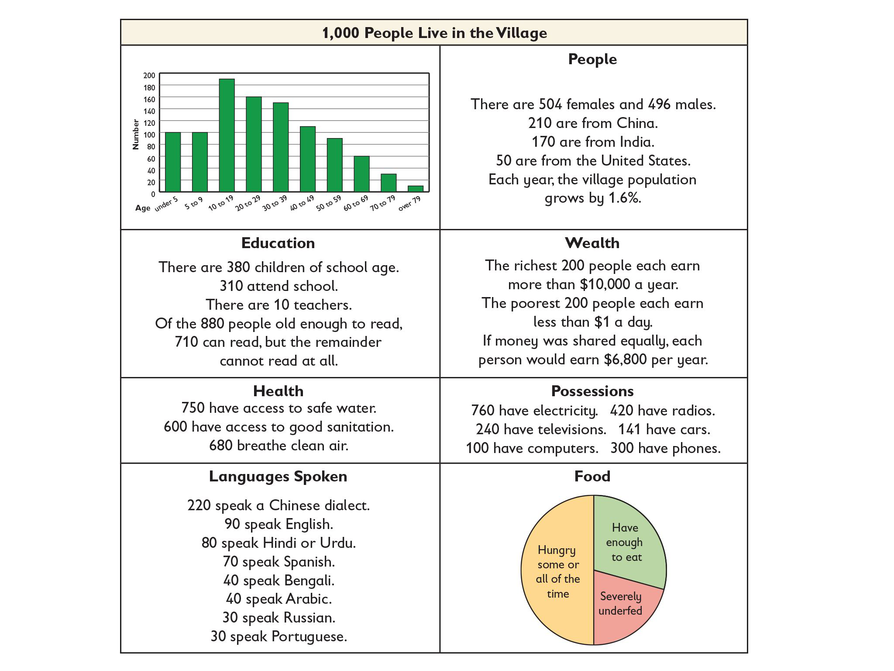
The Global Village
Lesson Guide
Have students examine the data in the chart carefully. Ask students to study two or three sections of the chart and then choose one category of data. Ask each student to write a statement with a percent in it about one category of data. Have students share and discuss their statements with a partner.
SWD: If students are demonstrating difficulty interpreting and analyzing the information in the representations of data (and the relationships between the data), highlight the columns that correlate. You can also color-code values to highlight how they relate to each other.
ELL: List all student responses, potential difficulties, and possible solutions for these problems. As students are working through the problems, they can refer to the list of difficulties and discuss ways of resolving them.
Mathematics
Students are asked to interpret data represented in different formats—bar chart, circle graph, rate statements, ratio statements, values, and words—and then write percent statements to represent the data. Ask:
- Does your percent statement represent the ratio of a part to a part or a part to the whole?
- What comparisons could your percent statement help you make?
Opening
The Global Village
In the world today there are more than 7 billion people. If the world were shrunk to the size of a village, what would it be like?
Imagine the Global Village described in the table.
- Choose one of the categories of data in the table, and write a statement in which you use percent to describe something about the data.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore and analyze data using percents.
Opening
Explore and analyze data using percents.
Explore the Global Village Using Percents
Lesson Guide
Have students work in pairs on the problems.
SWD: Students with disabilities may have difficulty working with parts and wholes when representing percents, especially moving between the two. If students demonstrate difficulty to the point of frustration, provide direct instruction on the basics for finding percents.
ELL: Allow students time to explain how they are doing what they are doing if it is not readily apparent when you observe.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Students are asked to challenge their partners’ explanations if they are not clear, correct, and complete; listen for efforts to clarify and build on one another’s arguments for why a statement is true, false, or cannot be determined to be true or false.
Interventions
Student has difficulty getting started due to difficulty interpreting or understanding the statements on the cards.
- Read the statement on the card aloud to your partner.
- Rewrite the statements as expressions, using values and letters instead of words.
- Rewrite the statements by converting the percents to decimals or fractions.
Student has difficulty getting started due to difficulty interpreting or understanding the way the data is presented (e.g., bar chart, ratio statement).
- Ages (bar chart): What does the height of each bar represent?
- Ages (bar chart): If you added all of the bars together, what would be the total amount?
- Ages (bar chart): If you add all the bars representing the three oldest age groups, what would that number tell you?
- Education (ratio statements): Which of the numbers in this category add up to the total Global Village population of 1,000?
- Education (ratio statements): Which of the numbers in this category represent parts of other quantities within this category?
For Card C, student doesn’t recognize what to treat as the “whole” and as a result misidentifies the statement as false.
- Read the statement on the card aloud to your partner.
- What is the “whole” in this case, the Global Village population or a certain part of this population?
- In this statement, the “base” is different. It’s not the whole Global Village population, but one part of it. Use the correct base in your computation.
For Card D, student doesn’t recognize that households are a different unit from individuals and as a result misidentifies the statement as true.
- Read the statement on the card aloud to your partner.
- Is the statement about numbers of individual people, like the other statements so far?
- Do you know how many people are in a household in the Global Village? Think about why this number matters.
Answers
Work Time
Explore the Global Village Using Percents
Work with a partner.
- Take turns choosing a card. Based on the data in the Global Village table, decide whether the statement on the card belongs in the “True,” “False,” or “Cannot Tell” column.
- Explain to your partner how you made your decision. Your partner should either agree with your explanation or challenge it if they think your explanation is not clear, correct, or complete.
- When you both agree, move the card into the appropriate column.
- Take notes on your reasons for deciding whether the statement on the card is true, false, or if you cannot tell; include any relevant calculations.
- After you have placed all the cards, look at the cards in the “False” column. For each card, discuss with your partner what percent would make that statement true.
For some cards, you may need to add or subtract data in the Global Village table before you can calculate the percent given on the card.
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for the following student thinking to highlight during the Ways of Thinking discussion:
- Students who use a variety of strategies for determining whether percent statements are true or false
- Students who discuss whether the percent statements represent part-part ratios or part-whole ratios
- Students who discuss how to interpret the data presented in different formats
- Students who are clear about what operations are needed to check percent statements (e.g., when subtraction is appropriate and when division is appropriate)
Challenge Problem
Answers
- Possible answer: A population of 768 instead of 1,000 would make the activity more difficult because division by 768 is more difficult than division by 1,000, but the operations would have been the same.
- Possible answer: A world population of 8 billion would have made no difference, because the percents represent parts of the 1,000 Global Village population.
Work Time
Prepare a Presentation
Select three cards, one from each of the three different columns you placed the cards in. Explain why you placed them in those columns.
Challenge Problem
- Suppose the population of the Global Village is 786 instead of 1,000. Do you think the activity will be easier or more difficult using this new population? Explain your answer.
- Suppose the world population is over 8 billion instead of 7 billion. Also suppose the Global Village population is still 1,000 and the data for the Global Village population is the same. Do you think the activity will be easier or more difficult with this change? Explain your answer.
Make Connections
Mathematics
As students present different strategies for determining whether statements are true or false, ask the class to think about a way of describing a general process for checking percent statements. Encourage students to represent the statements in the form of expressions or equations. For example:
Card F:
0.25P = 0.25(1,000) = 250
1,000 − W = 250
Card E:
0.43P = 0.43(1,000) = 430
C + I + U = 430
Introduce the term “base” in this discussion when students refer to the “whole” population. (Note that for Card C, the base is the number of school-aged children.) To explore the given data further, ask:
- Can you tell just by looking at the Wealth data what percent of the population makes more than $10,000 per year? (Answer: Yes, 20%)
- Can you tell, in terms of percents, how many more people own cars than computers? (Answer: Yes, 4.1%)
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Invite at least one pair of students to describe a case where they clarified, corrected, and/or further developed one partner’s argument for why a card belonged in a certain column.
Mathematical Practice 4: Model with mathematics.
Point out that this lesson illustrated several ways of using mathematics to model something. Working with a sample of 1,000 people to represent the global population created a model that made investigating the global population easier.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Have students describe patterns in the reasoning involved in checking the truth of each card. Highlight regularities in their computations—for example, always carefully identifying the whole and the part and then dividing the part by the whole.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' strategies for evaluating the statements on the cards.
As your classmates present, ask questions such as:
- Did you use equations or expressions to test any of the statements on the cards? If so, how did doing this help you? If not, do you think using expressions or equations is a good idea?
- How do you think representing this type of data with percent statements helps people interpret data?
- Suppose a student thinks that the statement about 85% of school-aged children attending school represents a part-part relationship. How could you help the student think about the relationship more clearly?
Use Percents to Explore Data
A Possible Summary
Percent statements allow you to make comparisons between parts of a whole. When working with percents, it is essential to be clear about what the “whole” is. The whole is also called the “base.” Percent statements help you understand and interpret data and are useful in mathematical modeling.
Additional Discussion Points
If there is time, discuss the following:
- How students could tell whether a statement with a percent in it was true or false, or if they were unable to tell
Formative Assessment
Summary of the Math: Use Percents to Explore Data
Write a summary about how you used percents to analyze the Global Village data.
Check your summary.
- Do you describe the data in the Global Village table?
- Do you explain how you used percents to determine whether statements about data in the Global Village are true, false, or you can’t tell?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out other places and ways that students have seen percents used to report data.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Some other places and ways I have seen percents used to report data are …