Compound Events & Sample Spaces

Overview
Students begin learning about compound events by considering independent events. They will consider everyday objects with known probabilities. Students will represent sample spaces using lists, tables, and tree diagrams in order to calculate the probability of certain events.
Key Concepts
Compound events are introduced in this lesson, building upon what students have learned about determining sample space and probabilities of single events.
Terms introduced are:
- multistage experiment: an experiment in which more than one action is performed
- compound events: the combined results of multistage experiments
- independent events: compound events in which the outcome of one does not affect the outcome of the other
Goals and Learning Objectives
- Learn about compound events and sample spaces.
- Use different tools to find the sample space (tree diagrams, tables, lists) of a compound event.
- Use ratio and proportion to solve problems.
SWD: Go over the mathematical language used throughout the module. Make sure students use that language when discussing problems in this lesson.
Coin and Number Cube
Lesson Guide
Conduct an informal poll. Have students tell you yes or no as an answer to the Opening question. Share the class results.
Mathematics
Students are using their limited knowledge of probability and their intuition to see that this event is not very likely.
Discuss the Opening question as an introduction to compound events. Ask the following:
- If it is unlikely that you will get a heads-up and roll a 3 on the first try, how many trials do you think it will take before you do?
- How many times do you think a heads-up and a 3 will come up in 500 trials?
- What do we need to know to answer this question?
Explain that when two or more events happen at the same time, or one right after the other, this is called a compound event. Elicit from the students that all possible outcomes need to be found (remind students of the definition of probability) to determine the probability of the event.
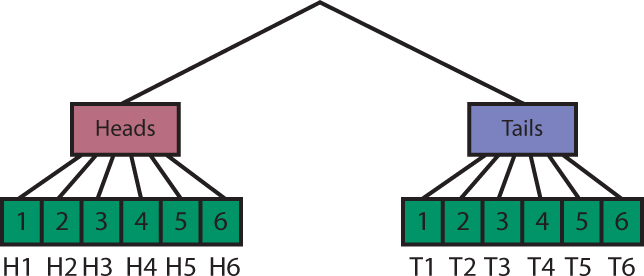
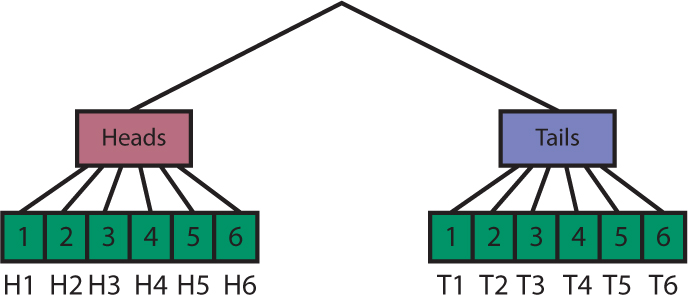
Give students a few minutes to list the outcomes and then discuss methods students used to ensure that all outcomes have been determined. Share the idea of a systematic list, in which students list every possibility. In this example of a coin toss, H stands for “heads” and T stands for “tails”:
H1| T1
H2| T2
H3| T3
H4| T4
H5| T5
H6| T6
There are 12 possible outcomes, with one favorable (H3), so the probability of the event is .
- ELL: Point to or highlight the parts of the tree diagram that you are referring to so that students can follow along with how the possible outcomes are displayed in the “branches” of the tree diagram.
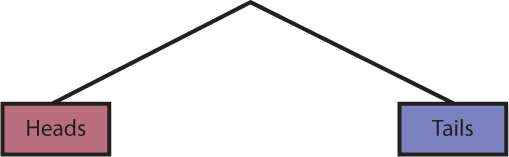
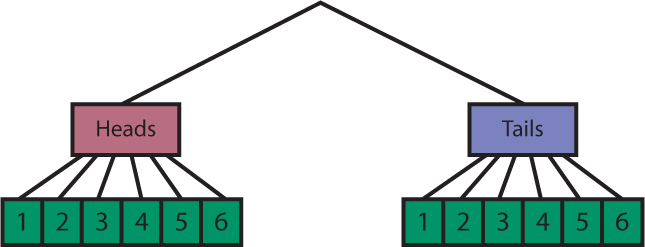
Explain that a list of possible outcomes is called the sample space. Demonstrate that the sample space can also be shown using a tree diagram. The outcomes for the first event are the first “branches” of the tree:
The outcomes for the second event are the next set of branches. For each way the coin can land, we could roll 1, 2, 3, 4, 5, or 6 on the number cube. These will be the next branches.
This gives us all of the combinations:
Opening
Coin and Number Cube
Suppose you conduct an experiment in which you toss a coin and roll a six-sided number cube.
- Do you think it is likely that you will get a heads-up and roll a 3 on the first try?
Multistage Experiments and Compound Events
Lesson Guide
Have students discuss the terms multistage experiment, compound events, and independence with a partner before leading a class discussion.
- ELL: Allow and encourage the use of dictionaries or translation sites should they need them to better understand the topic and to improve their use of academic vocabulary (especially for ELLs).
Mathematics
During the discussion, make sure these points are addressed:
- Multistage experiments can occur simultaneously or one at a time (both are given as examples). They are two distinct actions; that is what makes them multistage.
- Events are independent if the sample space of one event does not affect the sample space of the other.
Have students think about the number of outcomes for a multistage experiment, such as rolling two number cubes. They will be thinking more systematically now and are likely to use a list and the tree diagram as tools.
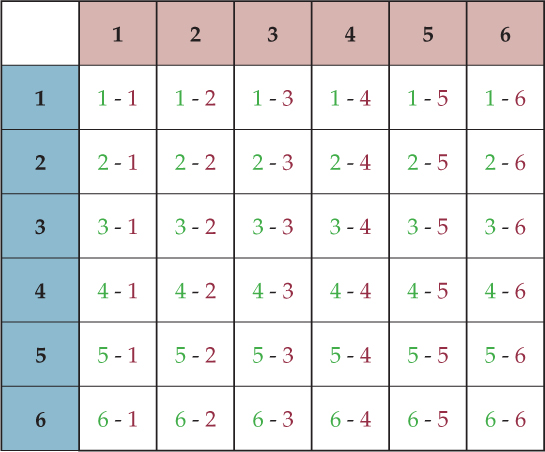
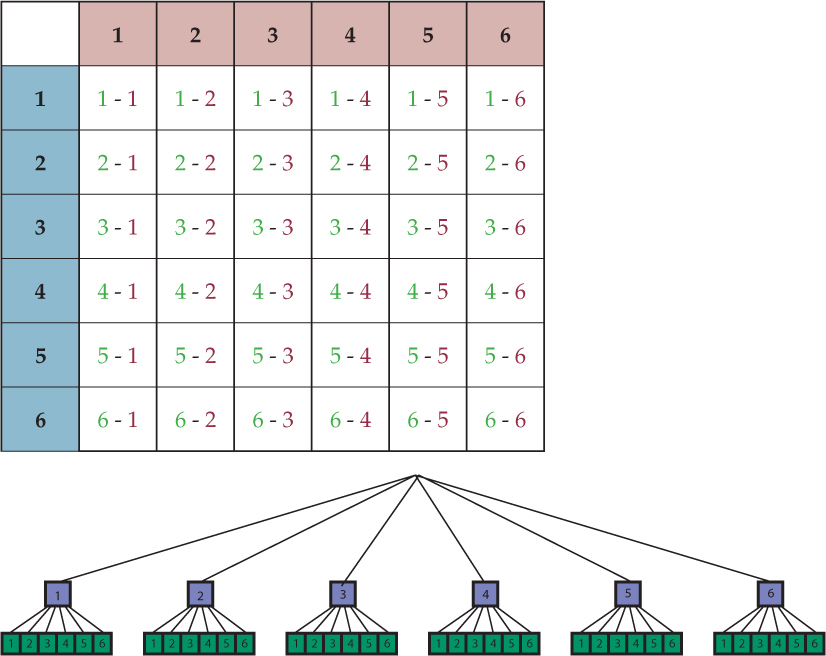
A list could be made, pairing each number on one cube with all of the numbers on the other cube:
1-1| 2-1| 3-1| 4-1| 5-1| 6-1
1-2| 2-2| 3-2| 4-2| 5-2| 6-2
1-3| 2-3| 3-3| 4-3| 5-3| 6-3
1-4| 2-4| 3-4| 4-4| 5-4| 6-4
1-5| 2-5| 3-5| 4-5| 5-5| 6-5
1-6| 2-6| 3-6| 4-6| 5-6| 6-6
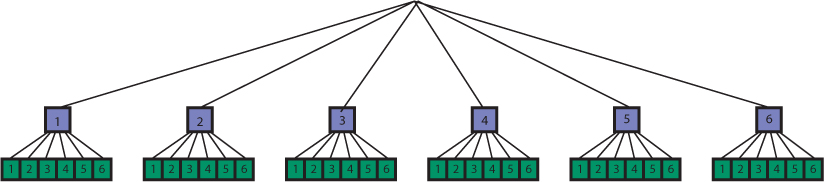
A tree diagram could be used:
However, the tree diagram is a bit cumbersome. Another option is a table:
Students may ask about the seeming repetition of rolls (such as 3-1 and 1-3). The colors in the table help demonstrate why these rolls are different.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Students are introduced to more terms that will allow them to communicate probability concepts.
Opening
Multistage Experiments and Compound Events
Discuss the following with your classmates.
A multistage experiment is an experiment in which more than one action is performed. Examples include:
- Randomly selecting two cards from a deck
- Tossing three coins
- Rolling two number cubes
- Randomly choosing four people from a larger group
Compound events are the combined results of multistage experiments. The two events are said to be independent if the occurrence of one event does not affect the outcome of the other event. Examples include:
- Selecting two cards: draw an ace, replace the ace, and draw a jack
- Tossing heads, tails, and heads
- Rolling a 6 and a 3 on two number cubes
- Choosing two tenth graders from a random selection of all the students in a high school
Math Mission
Lesson Guide
Discuss the Math Mission. Students will represent the outcomes of multistage experiments, and find the probability of compound events.
Opening
Represent the outcomes of multistage experiments, and find the probability of compound events.
Sophie’s Tree Diagram
Lesson Guide
Students will work in pairs. Remind students of the tools for finding the sample space (systematic list, tree diagram, table).
Interventions
Student has an incorrect solution for the theoretical probability.
- Did you check your work?
Answers
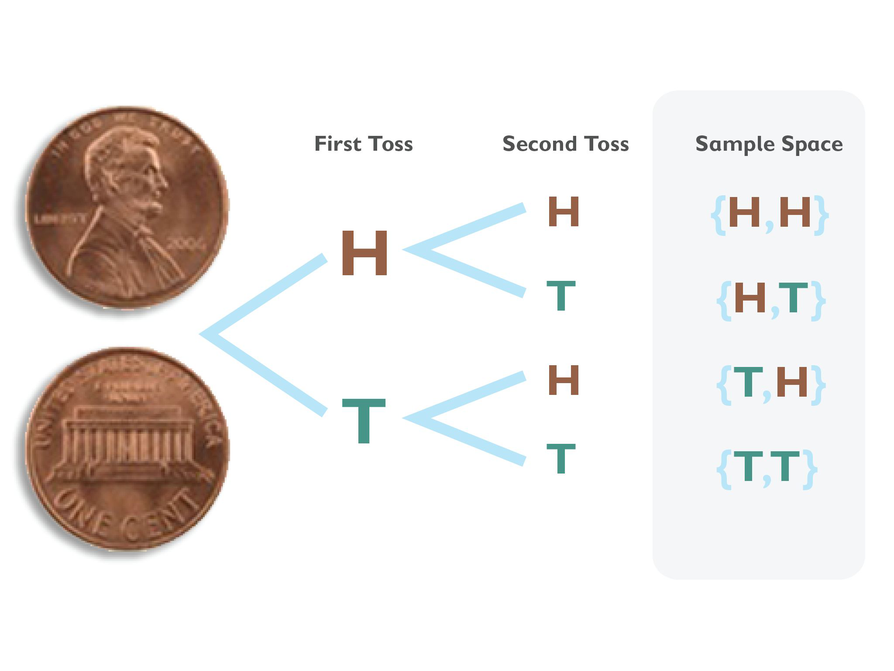
- The tree diagram shows four outcomes.
- Only one of the outcomes is {H, H}, so P(heads, heads) = = 0.25 = 25%.
- {H, T} and {T, H} are both favorable outcomes. P(heads and tails) = P(heads, tails) + P(tails, heads) = + = = 0.5 = 50%.
Work Time
Sophie’s Tree Diagram
Sophie conducted a multistage experiment in which she tossed a coin two times. She drew this tree diagram to represent the sample space.
- How many outcomes does the tree diagram show?
- What is the probability that Sophie will toss heads both times?
P(heads, heads) - What is the probability that Sophie will toss heads and tails in any order?
P(heads and tails)
Hint:
- How many outcomes are in the sample space?
- How many times does “heads, heads” appear in the sample space?
Jack’s Table
Lesson Guide
Students will work in pairs. Remind students of the tools for finding the sample space (systematic list, tree diagram, table).
SWD:Students with disabilities may require review and reinforcement for using the mathematical tools for probability. If needed, give students direct instruction on how to use the tools for finding the sample space.
Interventions
Student has an incorrect solution for the theoretical probability.
- Did you pair each of the first outcomes with each of the second outcomes?
- How many outcomes are favorable?
Student has a solution but does not provide an explanation.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problem.
Answers
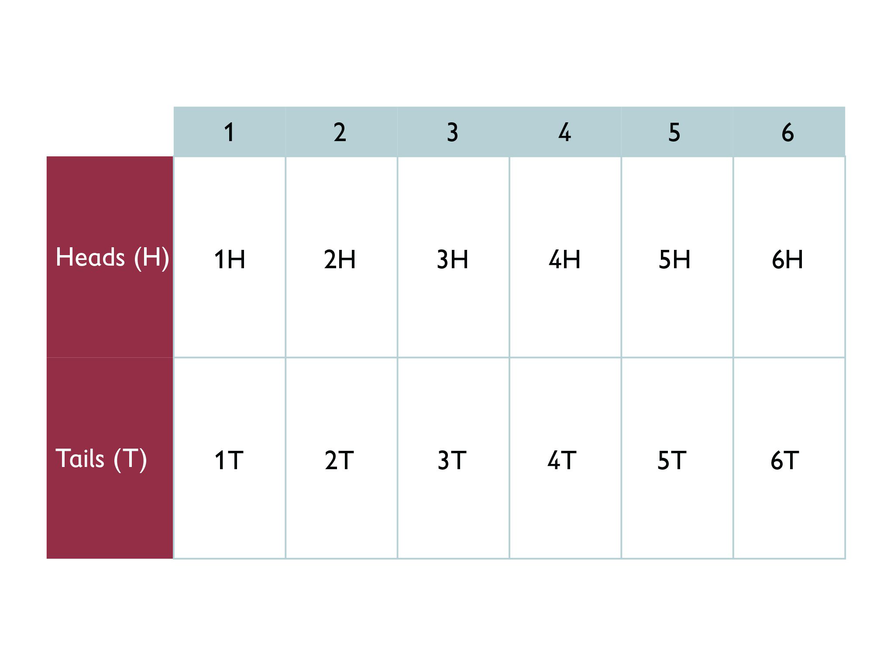
- There would be six outcomes if Jack just rolled the number cube.
- There would be two outcomes if Jack just tossed one coin.
- There are 12 outcomes in the table for both events.
- 1 and heads occurs only one time out of 12 outcomes on the table, so .
- 1 and tails occurs only one time out of 12 outcomes on the table, so .
Work Time
Jack’s Table
Jack conducted a multistage experiment in which he rolled a number cube and tossed a coin. Jack made this table to represent the sample space.
- How many outcomes would there be if Jack had only rolled the number cube?
- How many outcomes would there be if Jack had only tossed the coin?
- How many outcomes does the table show in the sample space for both events?
- What is the probability that Jack will get a 1 and heads?
P(1 and heads) - What is the probability that Jack will get a 1 and tails?
P(1 and tails)? - How many outcome cells do you see in the table?
- How many times do you see 1 and heads?
- How can you use the quantities from the previous two questions to calculate the probability?
Lucy’s List
Lesson Guide
Students will work in pairs.
Interventions
Student has a solution but does not provide an explanation.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problem.
Answers
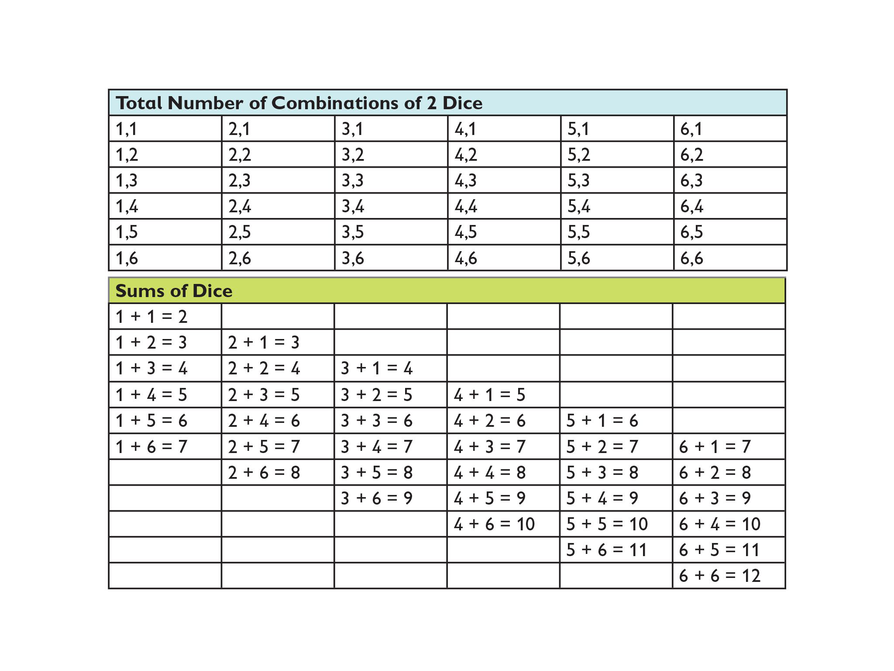
- There are 36 outcomes.
- Six of the outcomes add to 7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
- P(two numbers add to 7) = = = = %.
Work Time
Lucy’s List
Lucy conducted a multistage experiment in which she rolled two number cubes. She wanted to find the probability of rolling two numbers that add up to 7. Lucy first created a list of all the combinations of rolls. She then created a list of the totals for each combination.
- How many total outcomes are there?
- How many of those outcomes show two numbers that add up to 7?
- What is the probability that Lucy will roll two numbers that add up to 7?
Tree Diagram, Lists, and Tables
Lesson Guide
Students will work in pairs. Remind students of the tools for finding the sample space (systematic list, tree diagram, table).
SWD: Students with disabilities may require review and reinforcement for using the mathematical tools for probability. If needed, give students direct instruction on how to use the tools for finding the sample space.
Answers
Answers will vary. Students will answer with one of the six following representations:
The following are a list and table for Sophie's experiment: H-H H-T T-H T-T
H T H H, H H, T T T, H T, T List and tree diagram for Jack's experiment: H1| T1
H2| T2
H3| T3
H4| T4
H5| T5
H6| T6- Table and tree diagram for Lucy's experiment:
Work Time
Tree Diagram, Lists, and Tables
Sophie, Jack, and Lucy used a tree diagram, a table, and an organized list to help them find probabilities of compound events in their multistage experiments.
- Choose one of their experiments and represent the sample space using a different method. For example, Jack used a table to represent the number cube and coin outcomes. If you choose his experiment, use a tree diagram or an organized list to represent the outcomes.
Prepare a Presentation
Preparing for Ways of Thinking
As students prepare presentations, look for different problems and representations to share in Ways of Thinking, such as having a student present the solution to Jack's problem, then having another student present a different representation. Presentations should note how the representations are different, and why one might be preferred over another.
If any students did the Challenge Problem, have them also present.
ELL: When selecting a group of students to present in the Ways of Thinking, ensure students present a topic they are confident about. Have students include their tree diagrams or demonstrate their knowledge in some other way than through verbal language alone.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students extend their knowledge of probability by applying it to more complicated problems.
Mathematical Practice 7: Look for and make use of structure.
- Students should look for patterns or structures to construct lists, tables, or tree diagrams of the sample space.
Challenge Problem
Answers
- It is perhaps easiest to see the sample space by drawing a table:
P(roll a 5 and 7) = P(5, 7) + P(7, 5) = = = 2%
Work Time
Prepare a Presentation
- Prepare a presentation about the different ways of representing the probability of a compound event.
Challenge Problem
- If you roll two ten-sided number polyhedrons (sides labeled 0–9), what is the probability that you will roll a 5 and a 7?
Make Connections
Lesson Guide
Have students present solutions to the problems, as well as different representations of the same problem. Use this opportunity to clarify any confusion students have about creating representations of sample spaces or calculating probabilities.
Performance Task
Ways of Thinking: Make Connections
- Take notes about the probabilities students found and the ways they represented the outcomes.
Hint:
As your classmates present, ask questions such as:
- Why did you approach the problem the way you did?
- Which way of representing the outcomes do you think is easiest to work with? Explain.
- Can you solve the problem using a different method, e.g., using a tree diagram?
Multistage Experiments and Compound Events
Lesson Guide
Multistage experiments involve more than one action. The sample space for a multistage experiment can be represented as a list, table, or tree diagram. A compound event is one that combines outcomes from multistage experiments. The probability of a compound event can be calculated just like probability of a single event: the number of favorable outcomes divided by all outcomes.
Formative Assessment
Summary of the Math: Multistage Experiments and Compound Events
- Write a summary about multistage experiments and compound events.
Hint:
Check your summary:
- Do you define multistage experiment ?
- Do you explain what compound events are?
- Do you define sample space ?
- Do you describe the different ways to represent the outcomes in a multistage experiment?
- Do you explain how to find the probability of a compound event?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what examples of multistage experiments students propose.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Another example of a multistage experiment would be…