Gallery Problems Exercise

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Chance of Rain
Students are given the probability that it will rain on two different days and asked to find the chance that it will rain on one of the two days.
Penguins
In an Antarctic penguin colony, 200 penguins are tagged and released. A year later, 100 penguins are captured and 4 of them are tagged. Students determine how many penguins are in the colony.
How Many Yellow?
Given the total number of balls in a bag and the probability for two colors, students find the number of balls for the third color.
How Many Ways to Line Up?
Students decide how many different ways they five students can order themselves as they line up for class.
Gumballs
There are some white gumballs and red gumballs left in a machine. Students find the probability of getting at least one red gumball.
New Family
A married couple wants to have four children. Students find the probability that at least one child will be a girl.
Nickel and Dime
Students find the probability for different outcomes when tossing two coins.
Four More Flips
Students determine how many more tails are likely if a coin has already landed on tails twice.
Bubble Gum
The letters G, U, or M are printed inside bubble gum wrappers in a ratio of 3:2:1. Students use a simulation to find out how much bubble gum to buy to get a 3:2:1 ratio.
A Large Family
If a family wants to have six children, what is the probability that there will be three boys and three girls? Students use a simulation to model the probability.
No Telephone
Using census data from 1960 and 1990 in two box plots, students compare the percentages of families that had phones.
Pulse Rate
Students compare two data sets of different sizes: one for students and one for athletes.
Golf Scores
Students are given two sets of golf scores for Rosa and Chen. They are asked to decide who is the better golfer by constructing and comparing box plots.
How Much Taller?
Given two sets of data about heights, students determine how much taller one group is than the other.
Coin Jar
Students determine the contents of a coin jar by sampling.
Project Work Time
Students can choose to work on and complete their project or get help if needed.
Chance of Rain
Answers
- Possible solution:
Since the Saturday prediction and the Sunday prediction are independent events, we must consider four unequally likely possibilities: it will rain only on Saturday (0.16 chance); it will rain only on Sunday (0.16 chance); it will rain on both days (0.64 chance); and it will rain on neither day (0.04 chance).
The chance that it will rain on at least one of two days during the weekend is:
1 – 0.04 = 0.96 = 96%
Students could also use a tree diagram to think of the combinations. If we think of 80% as a 4 out of 5 chance, 4 of 5 outcomes are for rain. This makes 25 pairs of outcomes with only one outcome, no rain on both days, as being unfavorable:
In this task, students consider the sample space for two independent events in which the four possible outcomes are not equally likely. Students calculate the probability of a favorable outcome—when the result of at least one of the two events meets the stated criterion. In order to calculate correctly, students must consider that for some outcomes, results of both events meet the criterion.
Work Time
Chance of Rain
On Friday morning, Joey hears this weather report: There is an 80% chance of rain on Saturday and an 80% chance of rain on Sunday.
Joey says, “That means there is an 80% chance that it will rain on at least one day this weekend.” Joey is wrong.
- What is the chance that it will rain on at least one day during the weekend? Justify your answer mathematically.
Penguins
Answers
To solve this problem, it is best to use ratio and proportion. 200 penguins out of the whole population (which is unknown) are tagged: . In a sample, 4 out of 100 are tagged. These two ratios should be equal:
If the sample were representative, there would be 5,000 penguins in the colony. Students should see that it is likely that scientists would take more than one sample. If the colony is spread out, it would be helpful to get data from different areas to have a more representative sample. This task requires students to make a reasonable estimate about the total number of penguins in the colony based on information from a sample. In a strong response, students will apply the idea of a random sample, recognizing and using a given ratio to make an estimate.
Work Time
Penguins
In an Antarctic penguin colony, 200 penguins are captured, tagged, and released. A year later, 100 penguins are captured, and 4 of them have the tags from the year before.
- Based on this sample, how many penguins are in the colony?
- Does this sample provide enough evidence to make a reasonable estimate about how many penguins are in the colony?
How Many Yellow?
Answers
- The number of yellow balls is 16.
This task requires students to make part-to-whole comparisons to find a missing quantity in a probability situation. Students may compare the two given parts to the whole to calculate the missing part and then convert that to a quantity. Or they may find the individual quantities for each given part first. The task shows numbers in fraction form; students may do their work using fractions or decimals.
Whatever method students use, it requires the recognition that the given outcomes are the only ones possible and that the sum of the three outcomes totals one.
This task focuses on independent events (there is just one ball drawn, and the three outcomes—for red, green, and yellow—are mutually exclusive). The outcomes are not equally likely (red is most likely to be drawn and yellow least likely). Implicit here is the concept that the sum of the probabilities of all the outcomes equals one, since the only possible outcomes are red, green, and yellow.
Basic to this task is the realization that the three outcomes are not equally likely. Though the different probabilities of the three outcomes seem obvious, it may be far from obvious to students whose probability experience has been confined to situations with equally likely outcomes. (Dice and coins, though they can provide a context for good questions involving unequally likely outcomes, are too often used only to ask questions about equally likely outcomes.)
This task allows discussion of area models, useful in visualizing and solving probability problems. Area models illustrate and provide the ability to “count” the probability of each outcome. By dividing up the rectangle's length and width according to the denominators in the given probabilities (in this task, thirds and fifths), the result is inevitably a number of cells that is common to the two denominators (and in this case, 15 is also the least common denominator, since 3 and 5 are relatively prime). We can then use the area model to allocate cells for the given probabilities and assign the remainder to the unknown probability.
This task allows further discussion of other quantities that can be found on the basis of the given information:
- How many balls are not yellow?
- How many balls are either green or yellow?
- How many balls are neither yellow nor red?
This same situation also supports more conceptually advanced work on dependent events: what is the probability that, on two successive draws, I choose a yellow and then a green ball? (Assume each ball is returned to the bag before the next draw.)
Finally, it is important that students realize that an exact solution to “How Many Yellow?” is possible only because the reader is given the total number of balls and the theoretical probability for two of the three outcomes (and can derive the third). If, instead, students had been given experimental data (e.g., the results of pulling 10 balls, with replacement assumed each time) and the total number of balls, they could only answer based on the data. The actual number of yellow balls could turn out to be quite different from the predicted number, especially with a small data set.
Work Time
How Many Yellow?
There are 60 balls in a bag. Each ball is red, green, or yellow.
The probability of drawing a red ball is .
The probability of drawing a green ball is .
- How many yellow balls are there in the bag? Justify your answer mathematically.
How Many Ways to Line Up?
Answers
- There are 24 ways if Al is the first person in line. Here is a systematic list to find the number of ways that Al can be the first person in line:
ABCDE | ACBDE | ADBCE | AEBCD
---|---|---|---
ABCED | ACBED | ADBEC | AEBDC
ABDCE | ACDBE | ADCBE | AECBD
ABDEC | ACDEB | ADCEB | AECDB
ABECD | ACEBD | ADEBC | AEDBC
ABEDC | ACEDB | ADECB | AEDCB - There are six possibilities if Al is first and Bob is second. See the systematic list from the first question.
- A systematic way to solve this problem is to write out all the possibilities or write out the first set of possibilities (see the answer to problem 1). Then multiply the number of possibilities in the first set (24) by 5 (because we want to consider all the possibilities, not just those with Al first, and there are 5 students who can be in the first position), which gives 120 different possibilities in total. There are 120 ways for the students to line up. The task asks students to find outcomes and look for patterns. Students could begin with a simpler problem, starting with three students. They will see that there is one less choice at each level of the tree. For 3 students, there are 6 possibilities: 3 • 2 • 1 • 4 • 3 • 2 • 1 • 5 • 4 • 3 • 2 • 1 = 120. This task is as much about problem-solving strategies as it is about probability. Making a systematic list, looking for patterns, and solving a simpler problem can all be used as strategies to solve the problem. Students also get a look at permutations and the use of factorials.
Work Time
How Many Ways to Line Up?
Five students, Al, Bob, Carlos, Danica, and Ella, are early for math class and stand in line. They begin to talk about how many ways they could line up.
Find the number of ways that they can line up. Consider the following:
- How many ways are there if Al is first in line?
- How many ways are there if Al is first and Bob is second?
- Think of a systematic way to find all of the possibilities.
Gumballs
Gumballs
- Answers may vary. This task is similar to dependent compound events that students have done. The difference is that there are 72 total outcomes, so it is helpful for students to generalize and see the patterns in making a tree diagram. There are 9 outcomes for the first gumball and 8 for the second gumball, for a total of 72 outcomes:
9 • 8 = 72
3 • 8 = 24
3 • 6 = 18
Altogether there are 42 favorable outcomes:
24 + 18 = 42
Another way to look at the problem is by finding the complement of the event. The probability of drawing white twice (the only unfavorable outcomes) is because the 6 white gumballs can be paired with the 5 remaining white gumballs, for 30 outcomes:
Work Time
Gumballs
There are 3 red and 6 white gumballs left in a machine.
- If Sarah buys 2 gumballs, what are the chances that at least 1 gumball will be red? Show your work and justify your thinking.
New Family
Answers
Students need to find the sample space for the compound event. We can assume that boys are equally likely as girls to be born, so we could use the same tree diagram as we would use for flipping four coins. This is about the limit of practicality for using a tree diagram, so hopefully students are seeing patterns and powers of 2 in the combinations.
- There are 16 total outcomes, and 6 outcomes have 2 boys and 2 girls.
Work Time
New Family
A newly married couple wants to have 4 children.
- What is the probability that they will have 2 boys and 2 girls? Show your work and justify your thinking.
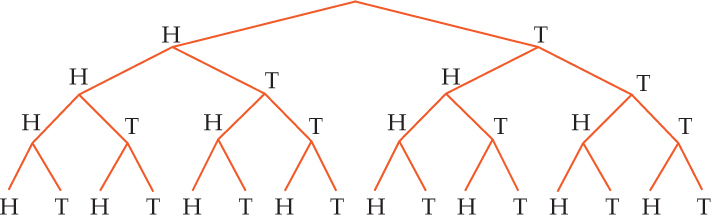
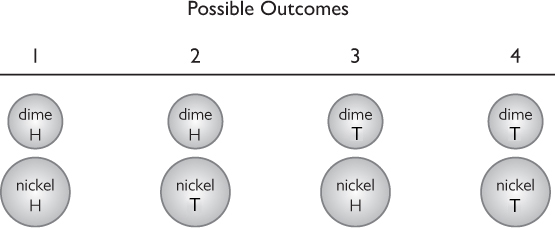
Nickel and Dime
Answers
- The probability that the nickel will land heads-up is .
- The probability that both coins will land heads-up is . For two coins, there are four equally likely outcomes, and only in one of them (the first outcome in the figure shown) do both coins land heads-up.
- The probability of only one coin landing heads-up is .
This task illuminates several kinds of confusion many students have when they begin to work with probabilities involving independent events. The task seems simple: there are just two coins, and flipping either coin gives one of only two equally likely outcomes. But case studies have shown that students whose understanding is tenuous can easily become confused by this task.
Students may be confused about what to count. There are lots of twos and fours in this task, but what do they mean? There are two heads, two tails, and two coins. There are four faces and four outcomes. Students are sometimes unsure which numbers are relevant.
Probability problems use very precise language. Two very similarly worded sentences will have different meanings. This can lead the student to give a correct answer to the wrong question.
Finally, students may know that they have to “do a calculation” when there are two independent events, but then do the wrong calculation. They may think, for example, that they need to add the probabilities of the two independent events.
To be able to avoid mistakes, students need a clear understanding of outcomes and sample space. Situations increase in complexity from a single event with equally likely outcomes (e.g., the likelihood of rolling a 2 with a single cube-shaped die) to multiple events with outcomes of differing likelihood (e.g., the likelihood that it will rain sometime during the weekend if there is a 25% chance of rain on Saturday and a 40% chance on Sunday).
In “Nickel and Dime,” the two different coins help students understand HT as different from TH, since they can recognize the head on a nickel as different from the head on a dime. This is less obvious when the two coins are of the same denomination. (Similarly, when using dice in probability work, you can start with two different-colored dice to help students distinguish between them.)
This task provides a starting point for a discussion of sample space and the different ways to represent it (e.g., an organized list, a tree diagram, an area model), as well as how to use these representations to answer questions about particular outcomes. You can initiate discussion with students about different correct representations.
Work Time
Nickel and Dime
Marisa flips a dime and a nickel at the same time. Both coins are fair―that is, the probability of getting heads is .
- What is the probability that the nickel is heads? Explain why.
- What is the probability that both coins are heads? Explain why.
- What is the probability that only one coin is heads? Explain why.
Four More Flips
Answers
- Of the 4 flips remaining, expect half to land tails. 2 tails from the first 2 flips + 2 tails from the remaining 4 flips = 4 tails. The most likely number of tails in the set of 6 flips is 4.
This task gives students coin-flip results for the first few trials of a stated number of trials. They are asked to predict the full set of results when all the trials have been completed. In any response that shows good conception, the student will consider the remaining trials independently rather than trying to adjust them based on the results of the first few trials.
Do events of the past affect the future? At the most basic level, students may understand that for a single coin flip, there is a 0.5 chance of a result of heads and the same chance of tails. At a slightly more advanced level, they may understand that for 20 flips, the likeliest set of results is 10 heads and 10 tails. But when faced with some number of trials that splits past and future results, students may be tempted to use the past results to “balance” the future ones, so that in the whole set there is a 50-50 allocation of heads and tails.
This attempt to balance past and future results is one manifestation of the “gambler's fallacy.” The gambler's fallacy is the incorrect assumption that the probability of a given outcome, with a fixed probability, will change based on recent events. For example, someone may think that if a coin flips heads 7 times in a row, the chance of a tails on the next flip is very high because the coin has to balance out with 7 tails. It's also possible that someone may think 7 heads in a row means that there is a high chance of heads on the next flip because it has been coming up heads very often. In reality, heads and tails both have a 50% chance of occurring on the next flip.
In order to think past the gambler's fallacy, students must understand that when we repeatedly flip a coin, the result of each new trial is independent of previous results. No matter what results we get from the first 99 flips in a set of 100 flips (whether 99 tails, 99 heads, or something else), the probability for the last flip is the same: a 0.5 chance that the result will be heads and a 0.5 chance that the result will be tails.
The task carefully asks what the most likely number of tails will be. Independent of the issue of whether future results can be expected to “even out” past ones, a student who suggests that 4 (or 3) is the most likely number of tails (as opposed to stating, “There will be 4 tails”) shows some understanding of the variability inherent in predicting actual results of random events.
Work Time
Four More Flips
Alex decides to flip a coin 6 times. He will record the results.
His first 2 flips are tails.
- After Alex flips the coin 4 more times, what is the most likely number of tails in his set of 6 flips? Justify your answer mathematically.
Bubble Gum
Answers
- Since the ratio of the letters is 3:2:1, a number cube could be used to simulate the outcomes:
G: 1, 2, 3
U: 4, 5
M: 6
Students roll and keep track of the number it takes to get each letter. After 20 or 30 trials, the students could construct a line plot of the data, finding the mean, median, mode, and range. This would give a pretty good idea of a typical number of packages to buy.
A box plot would also be useful since it shows the data in quartiles.
To answer the probability questions, we would need to look at the line plot and see what percentage of the trials is 10 or less. Usually this will be around 80%. To have a 50% chance of winning, you would have to buy the median number of packages. Usually, this will be around 6. If the students get different answers, check their work; this may present a good opportunity to discuss outliers.
The task shows students that complex probability problems can be modeled using experimental probability. In real-life applications, complex problems are modeled this way using computers.
Students should also understand that their data will be more reliable with more trials, and they should do as many trials as they can once they've drawn their initial conclusions to see if the additional trials reinforce the conclusions.
Work Time
Bubble Gum
A gum company has a contest. The winner is the first to collect the letters G, U, and M printed inside the bubble gum wrappers. One of the letters G, U, or M is printed inside each bubble gum wrapper in a ratio of 3:2:1. How many packages of bubble gum would you need to open to get each letter?
- Use a simulation to model the probability that you will win if you buy 10 packages of gum.
- How many packages would you need to buy to have a 50% chance of winning?
A Large Family
Answers
- Since we assume a 50% chance of having a boy or a girl, a coin can be flipped to simulate the event of having a boy or a girl. The student would flip a coin and keep track of the number it takes to get three girls.
To calculate the probability that out of 6 children, 3 would be girls, we would look at how many trials out of the total were 6 or less.
Students may see that a tree diagram could be constructed for 3 children, then 4, then 5, and so on. For 3 children, there is 1 favorable outcome out of 8. For 4 children, there are 4 out of 16. Analyzing the problem, students will see that it gets complicated quickly, yet a simulation can model the situation fairly easily.
Students should also understand that their data will be more reliable with more trials, and they should do as many trials as they can once they've drawn their initial conclusions, to see if the additional trials reinforce the conclusions.
Work Time
A Large Family
A newly married couple would like to have 3 girls. How many children are they likely to have in order to have 3 girls?
- Use a simulation to model the probability that they will have 3 girls by the time they have 6 children.
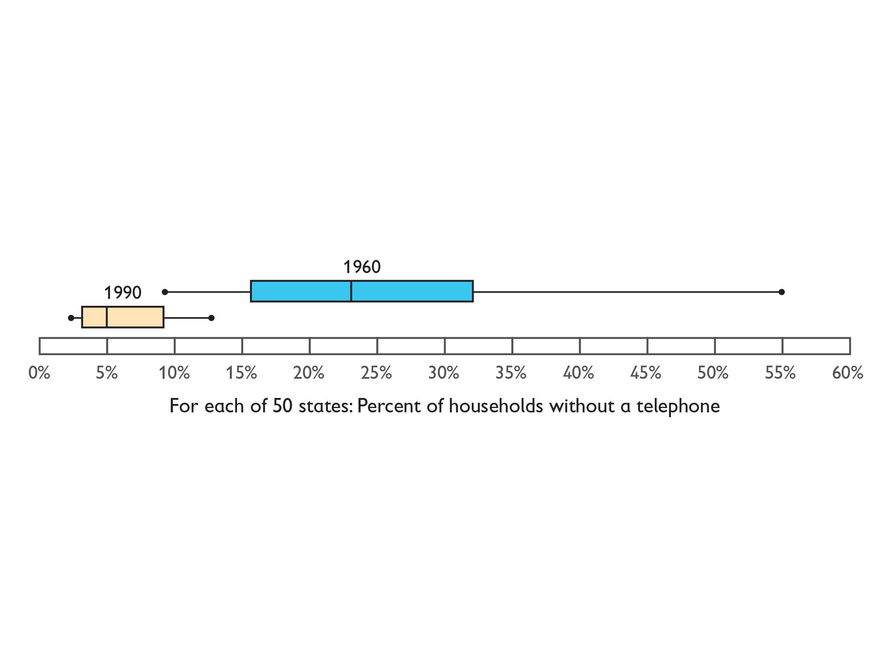
No Telephone
Answers
- Answers may vary. Possible answers may include:
- Large versus small range: The range between the “phone richest” and “phone poorest” states in 1960 is about 46%, about four times as great as the range in 1990. This means there is a great disparity among states: in 1960, there was at least one state in which fewer than half of the households had phones and at least one state in which more than 90% of the households had phones.
- Little overlap of the two ranges: In fact, the ranges are so different, with so little overlap, we can conclude that in most or all states, more households had phones in 1990 than in 1960. A percentage of household phones that would put a state in the top one-fourth of states in 1960 would put it in the bottom one-fourth in 1990. Substantial increase in phone ownership For all 50 states, the median in 1960 is about 77% of households with phones. The median in 1990 is about 95% of households with phones.
This task probes students' ability to interpret a pair of related box plots. Though students may explicitly mention the components of a box plot (e.g., mean, upper and lower quartiles, extremes), this is not the heart of this task. Rather, it is understanding the changes in phone ownership patterns depicted by the box plots and making and justifying correct conclusions.
Work Time
No Telephone
For each one of the 50 states, the U.S. Census Bureau reports the percent of households without a telephone. Some states have a higher percent of households without a telephone. Other states have lower percentages.
The box plots summarize these state-by-state data for two different years—1960 and 1990.
- What do the box plots tell you about how telephone ownership in the 50 states changed from 1960 to 1990? Give as much specific information as you can.
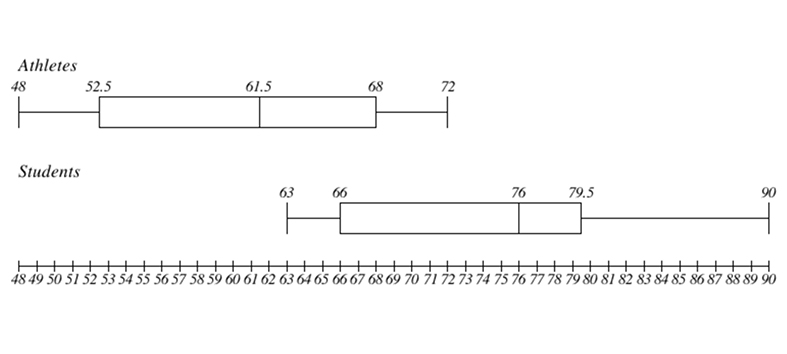
Pulse Rate
Answers
The data sets can be compared using box plots since they graph the data by quartiles and not the actual number of data values. This will compensate for the different size in the data sets.
The quartiles for each group are listed below, and can be seen in the box plots shown.
Athletes: Q1: 52.5; median: 61.5; Q3: 68
Students: Q1: 66; median: 76; Q3: 79.5
- It is fairly clear that the athletes have an overall lower pulse rate. The range for students is wide, and the extremes start higher than for athletes. The median for students is 76, and for athletes it is 61.5. Students could calculate the mean also, but they should see that it is not really necessary given the data in the box plot.
Although the results are fairly conclusive, students should understand that these are both pretty small samples and may not necessarily represent the population.
Work Time
Pulse Rate
The resting pulse rate (beats per minute) is shown for a group of athletes and for a group of students. Compare the two sets of data, taking into account that they are of different sizes.
Athletes: 48, 50, 52, 53, 56, 60, 63, 64, 66, 70, 71, 72
Students: 63, 66, 66, 74, 78, 79, 80, 90
- Which group has an overall lower heart rate?
Golf Scores
Answers
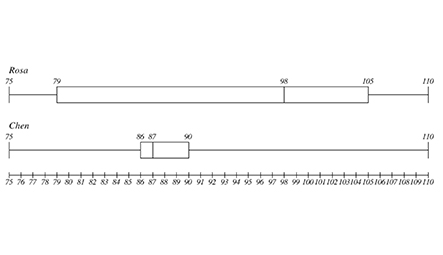
Rosa and Chen's scores in order are:
Rosa: 75, 79, 84, 98, 99, 105, 110
Chen: 75, 86, 86, 87, 88, 90, 110
Using these scores, the box plots are:
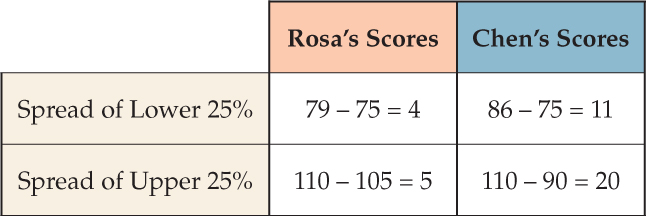
- The two data sets have the same minimum score (75) and the same maximum score (110). This means that they also have the same range (35).
- The interquartile range is spread in the central 50% of Rosa's scores than in the central 50% of Chen's scores.
- Chen's plot has a longer upper whisker. This information suggests that there is greater variability in the upper 25% of Chen's scores than in the upper 25% of Rosa's scores.
- Students may or may not conclude that Rosa's scores have a more symmetrical distribution. Of more importance is the reason they give for their decisions. They might look to see how close each median is to the center of the box. Or they might compare the lengths of the two whiskers and see that the spread of the higher 25% of Rosa's scores is more evenly matched with the spread of the lower 25% of her scores.
- Both golfers have the same range of scores, but comparing the medians leads to the conclusion that Chen generally has lower scores, which in golf means he has the better scores. Also, Chen's interquartile range is much less than Rosa's interquartile range, which can lead to a conclusion that Chen is a more consistent golfer.
Work Time
Golf Scores
Rosa and Chen love to play golf. Rosa’s scores for seven rounds were 105, 79, 98, 84, 75, 99, and 110. Chen’s scores were 88, 86, 90, 86, 75, 110, and 87.
Make two box plots to show the data. Be sure to use the same scale and align the same values with each other.
Compare and contrast the box plots.
- Which features of the two data sets are the same?
- Look at the interquartile range for both data sets. Use this statistic to comment on the golfing skills of Rosa and Chen.
- Compare the upper whiskers of both graphs. What does this information tell you?
- Which of the box plots is more symmetrical? What does this information tell you about the data distribution in the box plot?
- How do the medians, ranges, and interquartile ranges compare, and which of these statistics tell you who the better golfer is? Explain your answer.
How Much Taller?
Answers
A box plot is probably the simplest way to compare the two sets of data. A line plot would be flat because only data value repeats in either data set. The box plot will show the spread of the data and how the data sets compare to each other.
First, the quartiles:
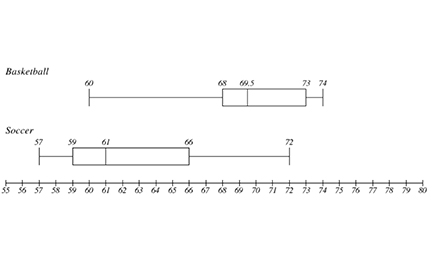
Basketball: Q1: 68; median: 69.5; Q3: 73
Soccer: Q1: 59; median: 61; Q3: 66
From the box plots, we can see that both groups have a similar range, but the interquartile ranges don't even overlap. The median for the basketball players is much higher (69.5) than for the soccer players (61). Both groups have an outlier that makes both ranges appear similar.
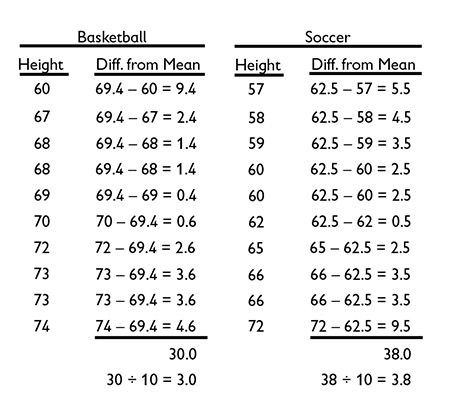
Students are also asked to find the MAD.
The MADs for both groups are pretty close, so both sets of data deviate from the mean by about the same amount. Each set of data is about as reliable as the other. This reinforces the mean as a valid measure. In addition, the mean for each group is close to the median. The mean for the basketball players is about 7 inches higher than the mean for the soccer players.
Students should notice that the MAD is one more tool that helps show the spread of data. Like other tools, it is useful in some situations and not in others.
Work Time
How Much Taller?
Basketball: 60, 67, 68, 68, 69, 70, 72, 73, 73, 74
Soccer: 57, 58, 59, 60, 60, 62, 65, 66, 66, 72
- Given the heights of the seventh-grade basketball team and the seventh-grade soccer team, in inches, decide which group is taller using the statistics tools of your choice.
- Calculate the MAD for both groups.
Coin Jar
Answers
- There are several ratios to consider. First, we'll find the weight of each stack of coins.
The whole sample weighs 1391.7 g (762.5g + 390.0g + 74.8g + 164.4g).
Each of these weights can be divided by the weight of the coin to find the number of that coin in the jar.
Next, each number of coins is multiplied by its value:
Students who attempt this task need to be very comfortable using ratios and proportions, as well as have good number sense. It's easy to lose track of the numbers, and it's important to work step by step. The actual total in the jar is a little over $84.
Work Time
Coin Jar
Given the sample, estimate how much money is in the jar.
Each coin weighs a specific amount:
Penny: 2.500 g
Nickel: 5.000 g
Dime: 2.268 g
Quarter: 5.670 g
- Think about the weight of each coin in the sample and what the ratio would be to the total weight of the sample and the coins in the jar.
Project Work Time
Help students as needed.
Project Work Time
You can choose to work on and complete your project and/or get help if needed.