- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Two Spinners
Comparing Theoretical & Experimental Probability

Overview
Students extend their understanding of compound events. They will compare experimental results to predicted results by calculating the probability of an event, then conducting an experiment.
Key Concepts
- Students apply their understanding of compound events to actual experiments.
- Students will see there is variability in actual results.
Goals and Learning Objectives
- Continue to explore compound independent events.
- Compare theoretical probability to experimental probability.
Coin and Number Cube
Lesson Guide
Have students talk briefly with a neighbor about the Opening question. Remind students that this same experiment was discussed in an earlier Opening (Lesson 6) about compound events.
Mathematics
Students have a greater knowledge of probability than the previous time this question was posed. Prompt students to describe two ways of solving the problem:
- Drawing a diagram (e.g., a list, table, or tree diagram)
- Using the formula P(A and B) = P(A) ⋅ P(B)
Discuss with students why one method would be preferable over the other.
SWD:Promote a language-rich environment in which students are encouraged to work together and learn from one another. Model the appropriate mathematical language at all times, and especially the use of new terms.
Opening
Coin and Number Cube
Suppose you toss a coin and roll a six-sided number cube.
- What is the theoretical probability that you will get heads and a 3?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will explore compound independent events by calculating and comparing expected and experimental results.
ELL: Ensure that ELLs understand the task by reading the directions aloud. Reading aloud is a metacognitive process that is invaluable to ELLs. This process is used to teach students how to predict, visualize, and tap in to their prior knowledge.
Opening
Explore compound independent events by calculating and comparing expected and experimental results.
Simulations of Coins
Lesson Guide
Students should work with a partner.
Interventions
Student has an incorrect solution for the theoretical probability
- How many outcomes are there for each event?
- Did you pair each of the first outcomes with each of the second outcomes?
- How many outcomes are favorable?
Answers
- Answers will vary. Possible answer:
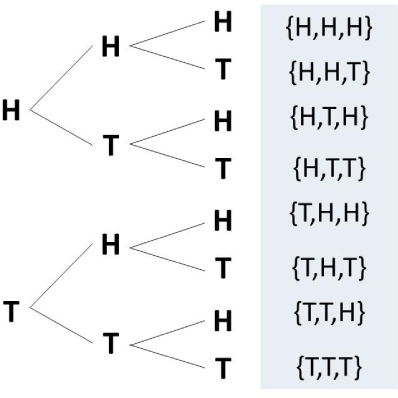
- P(1 head and 2 tails)=P(H, T, T)+P(T, H, T)+P(T, T, H)==0.375=37.5%
- In 100 trials, about 38 of them will be 1 head and 2 tails.
- Results for 100 trials will vary.
- Answers will vary when comparing expected to experimental results. Students should be able to address the discrepancy between them.
Work Time
Simulations of Coins
If you toss 3 coins, what is the probability that you will toss 1 heads and 2 tails?
- Create a diagram showing the sample space.
- Find the theoretical probability of the event.
- Predict the results for 100 trials.
- Perform 100 trials.
- How do your expected results compare to your experimental results?
INTERACTIVE: Three Coins
Simulations of Spinners
Lesson Guide
Students should work with a partner.
Interventions
Student has a solution but does not provide an explanation.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problem.
Possible Answers
Answers will vary. Possible answer:
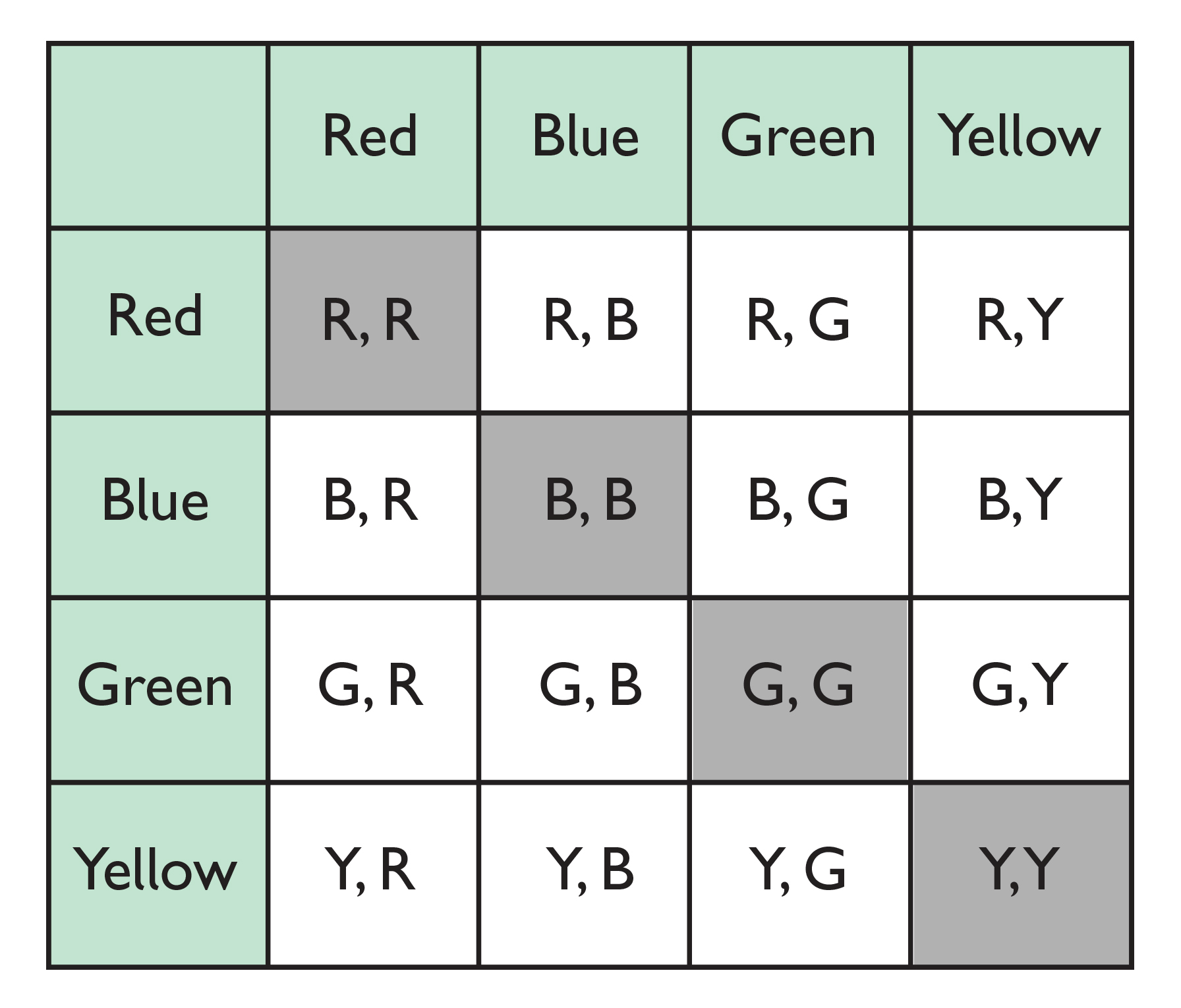
The desired outcomes are when the spinners match: {R,R}, {B,B}, {G,G}, {Y,Y}. Each of these outcomes occurs once, so P(spin matching colors) = = = 0.25 = 25%
- In 100 trials, the spinners will match about 25 times.
- Results for 100 trials will vary.
- Answers will vary when comparing expected to experimental results. Students should be able to address the discrepancy between them.
Work Time
Simulations of Spinners
If you spin 2 four-part spinners (each with the same, equal-sized sections and colors), what is the probability that you will spin matching colors?
- Create a diagram showing the sample space.
- Find the theoretical probability of the event.
- Predict the results for 100 trials.
- Perform 100 trials.
- How do your expected results compare to your experimental results?
INTERACTIVE: Two Spinners
Prepare a Presentation
Preparing for Ways of Thinking
As students prepare their presentations, look for students who used different sample space diagrams and offered different reasoning for the differences between theoretical probability and expected results.
If any pairs did the Challenge Problem, have them present a summary of the problem and solution.
ELL: When students work in pairs, it allows teachers to monitor individual student progress by listening and recording student conversations and peer problem solving. This type of collaborative work gives ELLs the opportunity to use mathematical language and to engage in conversation with their peers. Listen for student's reasoning regarding the differences between theoretical probability and expected results. Highlight these ideas during the Ways of Thinking section.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students continue to build their understanding and fluency by calculating the theoretical probability of events.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Presentations will vary. Presentations should show appropriate sample space diagrams, correctly calculate theoretical and experimental probability, and address the differences between the two.
Challenge Problem
Answers
- Answers will vary. Answers will depend on what problems students create.
Work Time
Prepare a Presentation
- Summarize your work for both problems: Show the sample space, provide the theoretical probability that you calculated, and explain your experimental results.
- Discuss your comparison of the theoretical probability and experimental results, justifying any conclusions you make with your work.
Challenge Problem
- Create a problem for your partner to solve that requires finding the probability of two compound independent events.
- Exchange problems with your partner and together reach an agreement for the answers to both problems.
Make Connections
Lesson Guide
While students are presenting, display the class totals for both experiments. Encourage students to ask the presenters about the differences between their individual sets of 100 trials and the much larger class set, and to theorize about why the differences are not very large.
SWD: Students must feel safe enough to share their ideas, strategies, and, most importantly, mistakes. Most students—and students with disabilities in particular—are not used to talking about mathematics; yet in higher-level courses, student success might depend on participation in study groups and the student's ability to share ideas.
Mathematics
Students are running a sufficiently large enough number of trials that their results should be very similar to the results of all the trials. Although this unit does not teach a formal method for calculating appropriate sample size, students will begin to build an intuition about this as they continue to compare experiments of varying trial sizes and sample spaces.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- When comparing predicted and actual results, students must make sense of the information and construct arguments about their observations. Students must also make sense of the differences between their experimental results and those of other students.
Performance Task
Ways of Thinking: Make Connections
Take notes about how your classmates' expected results compare to their experimental results.
As your classmates present, ask questions such as:
- How did you find the sample space and the number of favorable outcomes?
- Can you explain what your diagram of the sample space tells us?
- How did you decide what the expected results would be?
- How do your results for 100 trials compare with your expected results?
- Why do you think your expected results and experimental results compare in this way?
- How do your results for 100 trials compare to the class results?
- Which results—your results or the class results—are closer to the theoretical probability? Explain.
Compound Events
Lesson Guide
Have students discuss the summary with a partner before turning to a whole class discussion. Use this opportunity to correct or clarify misconceptions.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Students are introduced to additional probability terminology to use.
Formative Assessment
Summary of the Math: Compound Events
Read and Discuss
Multistage experiments result in compound events. Compound events are are composed of independent events if the occurrence of one event does not affect the outcome of the other event—that is, if the probability of one event is unrelated to the probability of the other event.
The sample space of a multistage experiment is the set of all possible outcomes of that experiment. You can represent the sample space of a multistage experiment using tree diagrams, lists, and tables, and use these representations to find the probability of compound events.
If you simulate a multistage experiment, the larger the sample size you use, the closer your experimental results will be to the expected results (the theoretical probability).
Can you:
- Define independent events?
- Explain how you can use representations of the sample space to find the probability of compound events?
- Explain the difference between expected results (theoretical probability) and experimental results?
- Explain how sample size affects experimental results?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to find out what students still do not understand about probability.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
Something I still do not understand about probability is...