- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Wheel
Calculating Probability As A Ratio

Overview
Students begin to formalize their understanding of probability. They are introduced to the concept of probability as a measure of likelihood and how to calculate probability as a ratio. The terms discussed (impossible, certain, etc.) in Lesson 1 are given numerical values.
Key Concepts
- Students will think of probability as a ratio; it can be written as a fraction, decimal, or a percent ranging from 0 to 1.
- Students will think about ratio and proportion to predict results.
Goals and Learning Objectives
- Define probability as a measure of likelihood and the ratio of favorable outcomes to the total number of outcomes for an event.
- Predict results based on theoretical probability using ratio and proportion.
Who Is More Likely to Win?
Lesson Guide
Have students watch the video and discuss the questions with a partner. There will be a class discussion during the next part of the Opening.
ELL: When showing the video, monitor that the ELLs are following the meaning of what is presented. If necessary, pause the video and allow them to ask clarifying questions. Alternatively, ask questions to check for understanding about what they are watching.
Opening
Who Is More Likely to Win?
Watch the Wheel video.
- Who do you think is more likely to win? How do you know?
- Think about the situation, and then discuss your ideas with a partner.
VIDEO: Wheel
About Probability
Lesson Guide
Have students read and discuss the explanation of probability with a partner before leading a whole class discussion. Ask students to think of real-world examples that involve probability.
Mathematics
Have students consider the situation of flipping a coin. There are two possible equally-likely outcomes for this event: the coin will land heads-up or the coin will land tails-up. We can calculate the probability of having a coin land heads-up because:
Discuss other real-world examples and how you could calculate the probability for these events (e.g., correctly guessing the month of someone's birthday).
Return to the video, making sure that the following points are discussed:
- The first student (Jack) has four ways to win (5, 10, 15, and 20) out of 20 ways to spin.
- The second student (Sophie) has five ways to win (4, 8, 12, 16, and 20) out of 20 ways to spin.
- Probability is a measure of likelihood and is the ratio of favorable outcomes (the thing or things we'd like to happen, such as spinning a multiple of five) to the total number of equally-likely outcomes (20 ways to spin the spinner). This is also called the theoretical probability.
- There is a , or , chance that the first student (Jack) will win, and a , or , chance that the second student (Sophie) will win. These are the probabilities for each event.
- If we actually spun the spinner once, the second student (Sophie) has a better chance of winning, but will not necessarily win.
- If we spin the spinner 100 times, we can predict the first student (Jack) will win times, while the second student (Sophie) will win times.
- If the spinner lands on 20, then both win. However, they will need to spin again.
Opening
About Probability
Discuss the following with your classmates.
In everyday life, people often think about whether or not something might happen in the future. Many decisions are based on the chance or probability that a particular event may or may not occur.
Probability involves the study of events whose results are affected by chance. The probability of an event is expressed as a ratio that can be used to predict the likelihood of an event occurring. Probability ratios are values ranging from 0 to 1. Probability ratios may be represented as fractions, decimals, or percentages. If an event has a probability equal to 0, then it is impossible. If an event has a probability equal to 1, then it is certain.
The theoretical probability of a particular event A is the ratio of the number of ways that A can occur to the number of all possible outcomes.
This is represented by the probability formula:
P(A) =
where
- a is the number of ways that an event can occur
- n is the total possible outcomes
Probability is a number between 0 and 1 used to quantify likelihood for processes that have uncertain outcomes (such as tossing a coin, selecting a person at random from a group of people, or tossing a ball at a target).
Math Mission
Lesson Guide
Discuss the Math Mission. Students will find the probability of events.
Opening
Find the probability of events.
Assign Probabilities
Lesson Guide
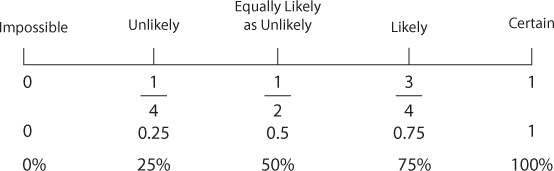
Students discuss what values should be assigned to Impossible, Certain, and Equally Unlikely before students mark events on the likelihood line in the Assigning Probabilities handout. Then students work individually on the remaining problems, but they may discuss with a partner.
ELL: This is a good opportunity for students to share ideas with others by working cooperatively. This interaction helps students develop their second language.
Mathematics
Give students an opportunity to think about how the marks on the likelihood line should be labeled.
Ask students:
- What values should be given to Impossible, Certain, and Equally Likely as Unlikely?
- What value should be given to the halfway mark between Impossible and Equally Likely as Unlikely?
- What value should be given to the halfway mark between Equally Likely as Unlikely and Certain?
Give students a few minutes to assign probability to each of the events. Students will discuss their reasoning in Ways of Thinking.
Answers
Remind students that a ratio can be expressed as a fraction, decimal, or a percent. Ask students to give the decimal and percent equivalents for each ratio on the likelihood line.
Answers will vary
- Most students' answers should fall within a narrow range (depending on whether it has been rainy, dry, or neither recently).
- Answers will vary from student to student. Some students may note that it is certain because they have already sent a text message earlier in the day.
- Answers will vary slightly but should all indicate a very low chance (very close to 0 on the likelihood line).
Work Time
Assign Probabilities
The Assigning Probabilities handout shows a likelihood line that is similar to the one you used in the last lesson.
- How should the marks for Imposssible, Certain, and Equally Likely as Unlikely be labeled?
- On the likelihood line, assign a probability from 0 to 1 for these events. Mark each of these events on the line.
- It will rain tomorrow.
- You will send a text sometime today.
- Out of all the students at your school, you will be chosen at random to win a prize.
HANDOUT: Assigning Probabilities
Probability of an Event
Lesson Guide
Students should work individually.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students are just beginning to approach probability problems. In the previous lesson, discussion centered on general observations of familiar situations. In this lesson, students must begin to represent probability experiments mathematically. They must make sense of these problems, and understand how to approach them.
Mathematical Practice 6: Attend to precision.
- Students must understand and explain the ratio and what the numerator and denominator represent. They also begin to apply probability terms.
Interventions
Student does not understand the problem.
- What is the probability formula?
- What does the formula represent?
Student does not correctly represent the ratio.
- How many ways can you roll a 3?
- What should the numerator of the fraction be?
- How many possible outcomes are there if you roll a number cube?
- What should the denominator of the fraction be?
Answers
- For this problem, students can apply the probability formula introduced in the Opening: P(A) = where P(A) = the probability of rolling a 3, a = 1 (the number of ways rolling a 3 can occur), n = 6 (the total possible equally-likely outcomes when rolling a number cube), and P(rolling a 3) = .
Work Time
Probability of an Event
- What is the probability of this event: rolling a 3 on a number cube that has the numbers 1−6 on it?
Prepare a Presentation
Preparing for Ways of Thinking
- As students prepare their presentations, look for students who can explain what the ratio represents. Look for students who can discuss their answer to the Challenge Problem.
Challenge Problem
Possible Answers
- Answers will vary. Possible answer: It is very unlikely that my house will be struck by lightening this year, so the probability will be very low.
- One way to calculate this would be to see how many houses in my neighborhood were struck by lightning last year. Then I can calculate:
Work Time
Prepare a Presentation
Prepare a presentation that summarizes how to express the probability of an event as a ratio.
Challenge Problem
- What is the probability that your house will be struck by lightning this year?
- How could you calculate the probability?
Make Connections
Lesson Guide
Begin by discussing the results from the probabilities students assigned to the likelihood line. Select a few students to present about the number cube problem. Have students who did the Challenge Problem present their answers.
SWD: Students with disabilities may struggle to follow the discussion and concurrently take notes during the Ways of Thinking portion of the lesson. Create scaffolded notes/questions based on the responses for some students. Use as a reference and support during the Ways of Thinking portion of the lesson.
Mathematics
Questions to ask about the likelihood lines:
- Was it harder to assign probability to some events compared to others? (Some events don't lend themselves to convenient ratios, a preview of events with no theoretical probability, but only experimental probability acquired over time.)
- How did you decide the probability for each event on the line? (The ratios could be determined several ways, but must be assigned in comparison to the location of the other events.)
Questions to ask during the number cube presentations:
- How many favorable outcomes were there?
- How many total outcomes were there?
Questions to ask while students explain their reasoning about the Challenge Problem:
- If there is a 1 in 200 chance of your house being struck by lightning sometime this year, where would this go on the likelihood line?
- If it is difficult to apply the probability formula, what are other ways to determine the probability?
Performance Task
Ways of Thinking: Make Connections
Take notes about calculating probabilities.
Hint:
As your classmates present, ask questions such as:
- Was it harder to assign probability to some events than others?
- For which events do you know the total number of outcomes?
- How did you decide the probability of each event on the line?
Calculate Probabilities
Lesson Guide
Students will work individually on the problems, but they may discuss with a partner. Encourage students to use the likelihood line tool if it is useful.
Mathematics
Students will calculate the probability for some common experiments. They should see that in some cases, the ratios could be simplified. As students work to predict outcomes for 120 trials, look for students who use ratios (fractions, decimals, or percentages) and those that are estimating (possibly thinking about ratios or what might actually happen).
Predicting results for 120 trials is purposefully ambiguous so that some students may think to use ratios (thinking of what would theoretically happen) while others will think about what might actually happen. This aspect of probability is an interesting discussion and will be defined further in the next lesson.
ELL: Encourage ELLs to use their English speaking skills in class. At the same time allow for use of their language of origin to clarify concepts during partner work. New ELLs may benefit from partners who speak their same language of origin.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Students are introduced to the probability formula and begin to apply it. They must understand what components in a problem correspond to the numerator and denominator in order to apply the formula correctly.
Interventions
Student does not represent the event correctly on the likelihood line.
- Is the event closer to 0 or 1?
- Is the event to the right or left of ?
Student does not correctly represent the ratios.
- If the numerator is 1 and denominator gets bigger, does the fraction become larger or smaller?
- If the numerator of a fraction gets bigger, does the fraction become larger or smaller?
- As the number in the numerator gets closer to the number in the denominator, does the fraction get bigger or smaller?
- What ratio would be equal to ?
- What ratio would be equal to ?
Answers
- P(spinner lands on red) =
P(spinner lands on red) can also be represented as a percent and decimal: P(spinner lands on red) = 25% = 0.25 - P(drawing a diamond) = =
P(drawing a diamond) can also be represented as a percent and decimal:
P(drawing a diamond) = 25% = 0.25 - P(coin lands on heads) =
P(coin lands on heads) can also be represented as a percent and decimal:
P(coin lands on heads) = 50% = 0.5 - P(marble drawn is blue)
P(marble drawn is blue) can also be represented as a percent or a decimal:
P(marble drawn is blue)
- P(spinner lands on red). For an experiment repeated 120 times, the spinner would likely land on red 120 ⋅ 0.25 = 30 times. (Answers to this part will vary.)
P(drawing a diamond). For an experiment repeated 120 times, a diamond would likely be selected 120 ⋅ 0.25 = 30 times. (Answers to this part will vary.)
P(coin lands on heads). For an experiment repeated 120 times, a coin would likely land heads on 120 ⋅ 0.5 = 60 times. (Answers to this part will vary.)
P(marble drawn is blue). For an experiment repeated 120 times, a blue marble would likely be drawn 120 ⋅ = 40 times. (Answers to this part will vary.)
Work Time
Apply the Learning: Calculate Probabilities
- What is the theoretical probability of the following events?
- Having a spinner land on red on a 4-part spinner with equal-sized, different-colored sections
- Drawing a diamond from a regular 52-card deck of playing cards
- Flipping a coin and having it land on heads
- Drawing a blue marble from a bag with 6 red marbles, 4 blue marbles, and 2 green marbles
- For each of the events previously listed, how many times do you think the event would occur if you repeated the experiment 120 times?
Theoretical Probability
A Possible Summary
Probability is a measure of likelihood. If all outcomes have an equal chance of occurring, it is the ratio of favorable outcomes to total possible outcomes. The ratio can be expressed as a fraction, decimal, or percent. Theoretical probability can be used to help predict results, but the actual results will probably not be exactly what we predict.
Formative Assessment
Summary of the Math: Theoretical Probability
Write a summary about theoretical probability.
Hint:
Check your summary:
- Do you define probability ?
- Do you describe the ways that probability can be expressed?
- Do you explain how to calculate the theoretical probability of an event occurring?
Reflect on Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out what students don't understand about probability.
- SWD: Some students with disabilities may struggle to explain their mathematical reasoning and understanding in words. Provide sentence starters and/or paragraph frames to support students with this task.
Work Time
Reflection: Reflect on Your Work
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
What I don't understand about probability is...