Effects of A Nonrandom Sample

Overview
Students will apply their knowledge of statistics learned in sixth grade. They will determine the typical class score from a sample of the population, and reason about the representativeness of the sample.
Students analyze test score data from a fictitious seventh grade class and make generalizations about district-wide results. They then compare the data to a second seventh grade class and reason about whether these are random samples. Students will review measures of center and spread as they find evidence to draw conclusions about the data.
Key Concepts
- Sample size will be considered as it affects the conclusions of an analysis of a population.
- Students will review tools that they used in sixth grade to analyze data, such as measures of center and spread, and different types of graphs.
Goals and Learning Objectives
- Explore sample size.
- Look at the effects of using a nonrandom sample.
- Review tools used to analyze data.
Math Test Scores
Lesson Guide
In preparation, you might want to look at students' responses to the Work Time problems in Lesson 12, which introduced the concept of sampling. At this point, do not spend time going over the problems, since students are still developing these skills, but look at the problems they had difficulty with. If possible, embed in this Opening discussion the mathematics involved in those problems as you discuss the line plot displaying the district math text results in this Opening.
Students will then discuss the question with a partner.
Mathematics
Students may see that the line plot is a nonrandom sample, as well as not being large enough to represent the district population. Don't discuss this now, as the purpose is to analyze the data and generalize for the whole population based on the sample.
Discuss the Opening question briefly, in general terms. Allow students to go right into Work Time using whatever tools they choose. Part of the purpose of the lesson is to remind students of all of the ways they analyzed data in sixth grade and what tools they might use to generalize about the population. They should also see a connection to probability in how results for a large set of trials were predicted (using ratios and proportions).
SWD: Students with disabilities may have trouble utilizing the tools for organizing data on the tablet. Check to see if the tool has accessibility settings to accommodate students with fine motor difficulties. Also, review how to use the tool for students who may have forgotten.
Opening
Math Test Scores
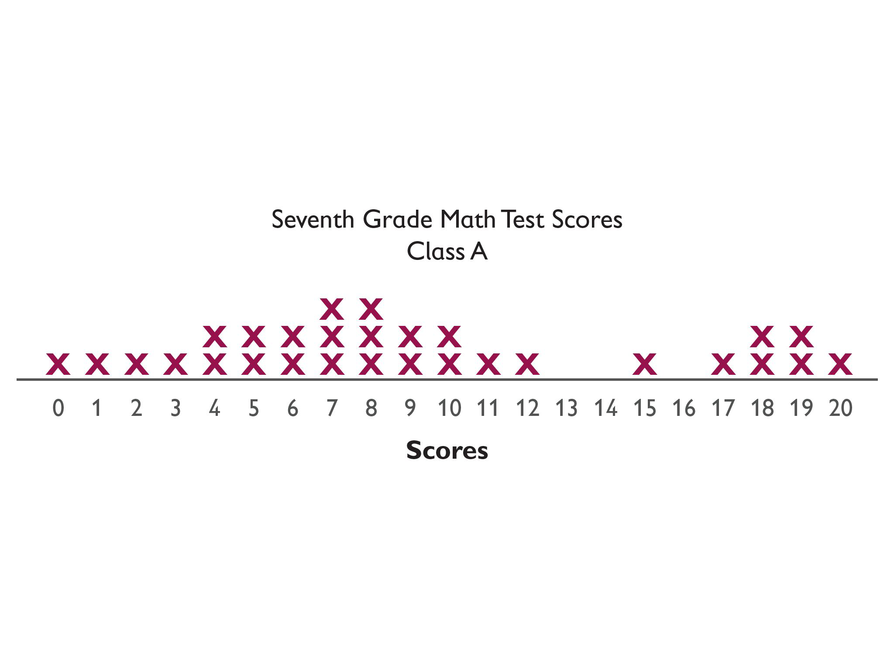
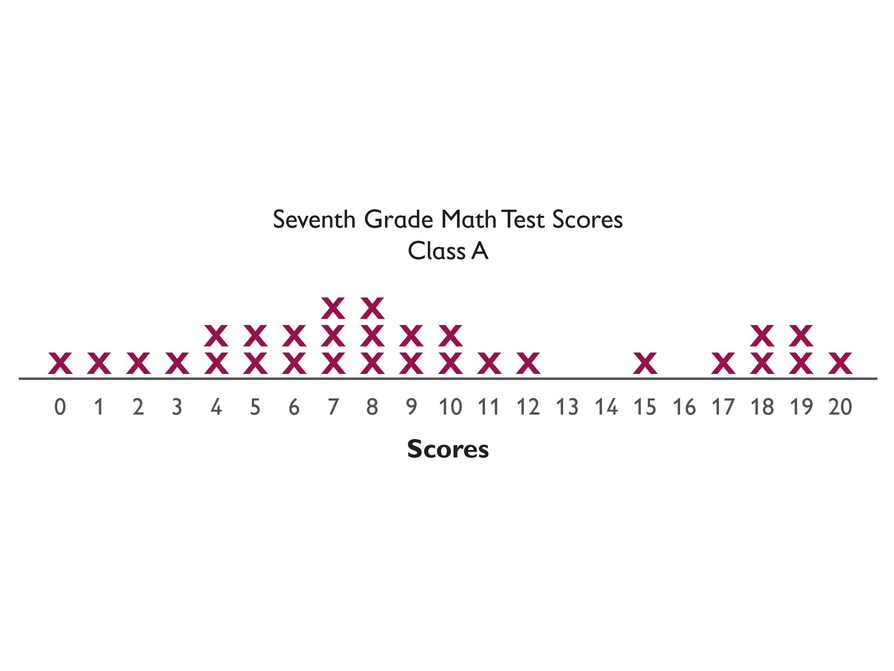
Every seventh grade student (870 total) in a school district takes the same math test. "X" represents one student in Class A. Based on the sample of Class A’s test results, how did all of the seventh graders in the district do on the test?
- Think about the question. Then discuss your ideas with a partner.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will analyze samples to make generalizations about a population.
Opening
Analyze samples to make generalizations about a population.
Make Generalizations About a Population
Lesson Guide
Students will work in pairs. They will explore the opening line plot.
ELL: Make sure you review the question's task with your students. Make sure students pay attention to the mathematical language in the problems given. Students need to know what words such as generalization mean when they are encountered in a problem. List these types of words on an anchor chart as a reference. Write what the word means, a definition, and an example of how it may be used.
ELL: Provide written questions, using a pace that is appropriate for non-English speakers. Introduce new vocabulary (e.g., generalizations and populations) at a slower pace to ensure understanding and recollection of meaning.
Mathematics
Students should see that the sample does not represent the population since it comes from one specific school in the district and may not represent all schools in the district.
Even though this sample is biased, students should use it to determine the characteristics of all seventh graders since this is the only data they have at this point.
As students work, look for different tools, methods, and graphs that students use to share in Ways of Thinking. The more variety the better, as this will remind students of ways they can analyze data.
Look for students who exhibit the following problem-solving strategies:
- Calculate the mean, median, and mode (measures of center) to describe the typical score
- Construct a box plot to show the middle 50% of data and other measures of spread
- Construct a histogram to represent the district results, using a bin width of one
- Construct a histogram to represent the district results, using a bin width greater than 1
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
There are many different ways to approach these problems. Students must be able to identify an appropriate method.
Mathematical Practice 5: Use appropriate tools strategically.
Students have many tools at their disposal. After they identify an appropriate method to solve the problem, they must identify and correctly use the appropriate tool.
Interventions
Student has trouble getting started.
- What are some of the tools you can use to analyze data?
- How many data points are on the line plot?
- How does that number compare to the total number of students in the district?
Answers
- Answers will vary. Possible answer: Line plot, measures of center (mean, median, mode), and box plot (measures of spread)
- Answers will vary. Possible answer: Calculating measures of center and spread can help us determine a typical score.
- mean: 9.24
- mode: 7, 8
- lower extreme: 0
- lower quartile: 5
- median: 8
- upper quartile: 13.5
- upper extreme: 20
- There is a cluster of high scores that pulls the mean toward the higher end of the range; the median (which is also a mode) would be a more appropriate typical score.
- The interquartile range is 8.5. [Interquartile range (IQR) = (Upper Quartile) – (Lower Quartile) = 13.5 – 5 = 8.5.]
- Answers will vary. Possible answers: In this class, 329 = 10.3% of the students scored an 8. 870 ⋅ 0.103 = 89.61, so if the sample is representative of the entire seventh grade, then about 90 students would score an 8.
Work Time
Make Generalizations About a Population
Use these test results for Class A to describe the seventh graders in the district (870 total).
Think of all the tools you can use to describe and analyze data—measures of center, measures of spread, line plots, box plots, and histograms—and how you might use these tools in this problem.
"X" represents one student in Class A.
Answer the following questions:
- Which tools do you think will be most helpful to you?
- What is the typical score on the district math test? How can you show this?
- Where do the middle 50% of the scores lie?
- About how many seventh grade students in the district would have the typical score?
- About how many seventh grade students would have each of the scores?
- What are some of the tools you can use to analyze data?
- Have you tried using any of the graphing tools?
- How many data points are on the line plot?
- How does that number compare to the total number of seventh grade students in the district?
- Does the sample represent the population of the district?
A Second Sample
Mathematics
Students should see that this sample does not represent the population either. They should see that both samples are biased because they come from specific schools in the district, which may have entirely different demographics.
Look for students who exhibit the following problem-solving strategies:
- Analyze the data sets for each class separately
- Aggregate the data sets and analyze them together
Interventions
Student does not conclude that the samples are not representative.
- Are the Class A scores a random sample of all the seventh grade scores? Why or why not?
- Are the Class B scores a random sample?
- Would combining the two sets of class scores give us a data set that is more or less representative?
Answers
The new measures of center and spread:
- Answers will vary. Possible answer:
- The measures of center and spread for Class B:
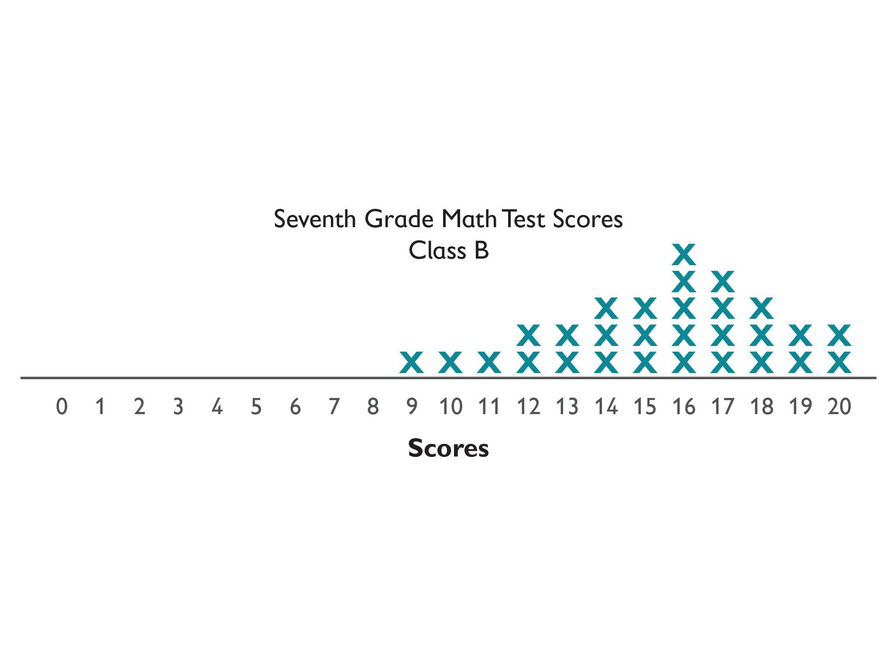
- mean: 15.41
- mode: 16
- lower extreme: 9
- lower quartile: 13.5
- median: 16
- upper quartile: 17.5
- upper extreme: 20
- Compared to Class B, Class A has a much larger range, and overall has lower scores. The distribution of scores is very different, implying that neither sample is representative of the entire seventh grade.
- The measures of center and spread for Class B:
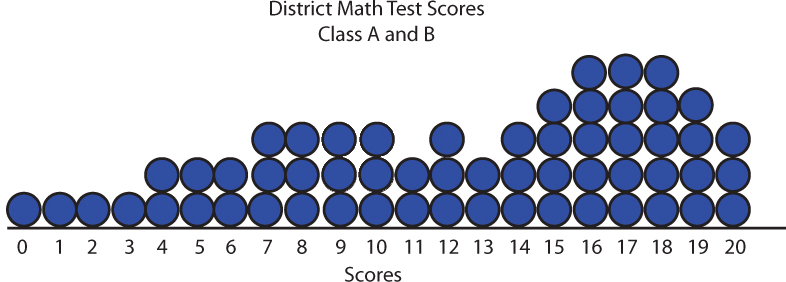
- Combining the data from the two classes makes for a larger sample, which will be more representative of the population.
- mean: 12.33
- mode: 16, 17, 18
- lower extreme: 0
- lower quartile: 8
- median: 13.5
- upper quartile: 17
- upper extreme: 20
The distribution of scores for the entire seventh grade:
Work Time
A Second Sample
Here is data from another seventh grade class, Class B, in the same district.
"X" represents one student in class B.
- What does this sample tell you about the first sample?
- How can you use this sample to help you make a better generalization about the population?
Prepare a Presentation
Lesson Guide
Students should be able to support their conclusions with evidence. They should also observe that the data set was not chosen randomly.
Look for students who answer the Challenge Problem in different ways. If necessary, offer up different ways to randomly sample during Ways of Thinking.
Step 1: Work Time
Prepare a Presentation
- Prepare a presentation about your conclusions for the results of all the seventh graders in the district.
- State how certain you are about your conclusions, and support your thinking with evidence.
Challenge Problem
Possible Answer
- Answers will vary. Possible answer: Assuming that there are about 30 students per class, there are probably 30 seventh grade classes in the district. If 5 students were randomly drawn from each class list, this would be a random sample of 150 students across the district.
To select the students in each class, you could roll a number cube and spin a 5-part spinner 5 times, since the sample space for that compound event is 30.
Step 2: Work Time
Challenge Problem
- How could you get a representative random sample of all the seventh grade results?
Make Connections
Lesson Guide
Have students present and explain their conclusions. If any students did the Challenge Problem, have them share methods for random sampling.
SWD: As students present their solutions, make connections between different solutions and methods to organize data to the same problem. This allows students to see the multiple ways to solve/analyze a problem. Make sure students provide justifications for their conclusions.
Mathematics
Consider these questions to pose during discussion:
- Was the mean, median, or mode a better indicator of the district score? Why?
- Where is the data clustered on each line plot? What is the range of the data?
- What does this tell you about the data, and possibly the sample?
- What was a typical score for Class A? For Class B?
- If the line plots are compared, which class performed better on the test? How do you know?
- Are either of these samples a random sample? Why?
- If you look at the combined results, is this a random sample?
- Are the combined results closer to showing how all seventh graders did on the test? Why?
- What would be a good way to get a random sample?
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
There will be many different answers to these problems. Students must be able to reason and defend their method as appropriate, even if it is different from others.
Performance Task
Ways of Thinking: Make Connections
Take notes about the different approaches your classmates used to describe and make conclusions about the data.
As your classmates present, ask questions such as:
- Which value is a better indicator of the typical score—the mean, median, or mode? Why?
- Where is the data clustered on the line plot? What is the range of the data?
- What does this information tell you about the data, and possibly the sample?
- What is a typical score for Class A? For Class B?
- Based on the line plots, which class performed better on the test? How do you know?
- Are either of these samples a random sample? Explain.
- Would you consider the combined results of the two samples to be a random sample?
- Are the combined class results closer than the separate class results to showing how all the seventh graders in the district did on the test? Explain.
Analyzing Samples
A Possible Summary
There are many tools that help us analyze data, such as line plots, box plots, and histograms. These tools can be used to observe the shape of data and calculate measures of center and spread. These tools allow us to analyze a sample and draw conclusions about the whole population. However, it is important that the sample is representative of the population, or the conclusions will not be valid.
SWD: Clearly summarize the lesson, and write down all salient information. Make sure students are recording Summary of Math notes in their notebook.
Formative Assessment
Summary of the Math: Analyzing Samples
Write a summary about analyzing and describing samples.
Check your summary.
- Do you list some of the tools available for analyzing data?
- Do you explain how you can use these tools to analyze a sample?
- Do you explain what a sample tells you about the population?
Reflect on Your Work
Lesson Guide
Have students write a brief reflection before the end of the class. Review the reflections to find out what information students can discern from graphs.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
When I look at a graph, I can tell these things about the data…