- Author:
- Chris Adcock
- Subject:
- Statistics and Probability
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 7
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Marble Jar
Sampling Experiments

Overview
Students begin to develop intuition about appropriate sample size by conducting an experiment. They compare different sample sizes and whether increasing the sample size improves the results.
Key Concepts
Sampling is a way to discover unknown characteristics about a population. The size of the sample is important in determining the accuracy of the results. Ratio and proportion are used to compare the sample to the population.
Goals and Learning Objectives
- Students will use sampling to determine the number of different color marbles in a jar.
- Students will explore sample size compared to population size.
500 Marbles
Lesson Guide
Show the jar of marbles and give students a few minutes to speculate about its contents, and then guess the number of marbles. Record your students' guesses by taking an informal poll. Make a bar graph of students' responses.
There are probably a range of guesses, indicating that there is not a consensus on the contents and students' estimation skills are varied. There is probably some agreement about which colors have the least amount, and which have the most.
Ask students how they can determine the contents of the jar without counting and sorting all of the marbles. Elicit from students that taking samples is one method they can use.
Mathematics
Students will have a rough idea of the proportions of colors in the jar, since it will be clear that there aren't very many red or green marbles and that there are a lot of yellow marbles. They will need to take samples to refine their guesses.
The Marble Jar has 500 marbles of 4 different colors:
250 yellow marbles (50%)
125 blue marbles (25%)
60 red marbles (12%)
65 green marbles (13%)
SWD: Help students with disabilities build their mathematical vocabulary by continually modeling the use of new terms in the context of classroom work and activities.
- sample size
- population
- estimation
Opening
500 Marbles
The glass jar contains 500 yellow, blue, red, and green marbles.
How many marbles of each color do you think there are in the jar? Record your guesses.
- Yellow __
- Blue __
- Red __
- Green __
Math Mission
Lesson Guide
Discuss the Math Mission. Students will determine the number of each color marble in a jar by analyzing samples, and explore the effect of sample size.
Opening
Determine the number of each color marble in a jar by analyzing samples, and explore the effect of sample size.
How Many Marbles?
Lesson Guide
Give students a few minutes to become familiar with the Marble Jar interactive individually. Students will work with a partner for the Work Time problems.
Mathematics
As students work, it will become apparent that a sample size of 10 is too small. Some of the samples are likely to not include all of the colors, which would give a misleading result. As the sample size increases, the results from sample to sample will become more consistent, indicating that the results are valid. Students will be interested to see how much or how little difference there is between the sample size of 50 and 100.
Students may ask about combining the samples, which should be part of the Ways of Thinking discussion. As the sample size increases, there is a higher probability that the same proportion of marbles is drawn.
As students work, they will begin to conclude that there are the same number of red as green, and that yellow makes up half of the contents of the jar. Look for students that are considering how the colors compare to each other proportionally.
SWD: Consider the prerequisite skills for this task/skill. Students with disabilities may need direct instruction on and guided practice with the skills needed to complete this task. Students will need to be able to set up proportions and solve.
ELL: When monitoring students, pay special attention to ELLs to ascertain that they are on task and clear about what needs to be done.
Interventions
Student has trouble finding the mean.
- What is the total of the red marbles in the five samples?
- How would you even them out among the five samples?
- What is the total for each color marble in the five samples?
Student has a wrong solution.
- What was the mean number of red marbles out of 10 marbles in the sample?
- How can you use this ratio to find the number of red marbles out of 500?
- What was the mean for each of the colors out of 10?
Student has a solution but does not provide an explanation.
- Why did you approach the problem the way you did?
- Explain your strategy for solving the problem.
- How do you know that you predicted the numbers correctly?
Answers
Answers will vary, depending on the samples that students draw. For each part, student answers should look something like the example below:
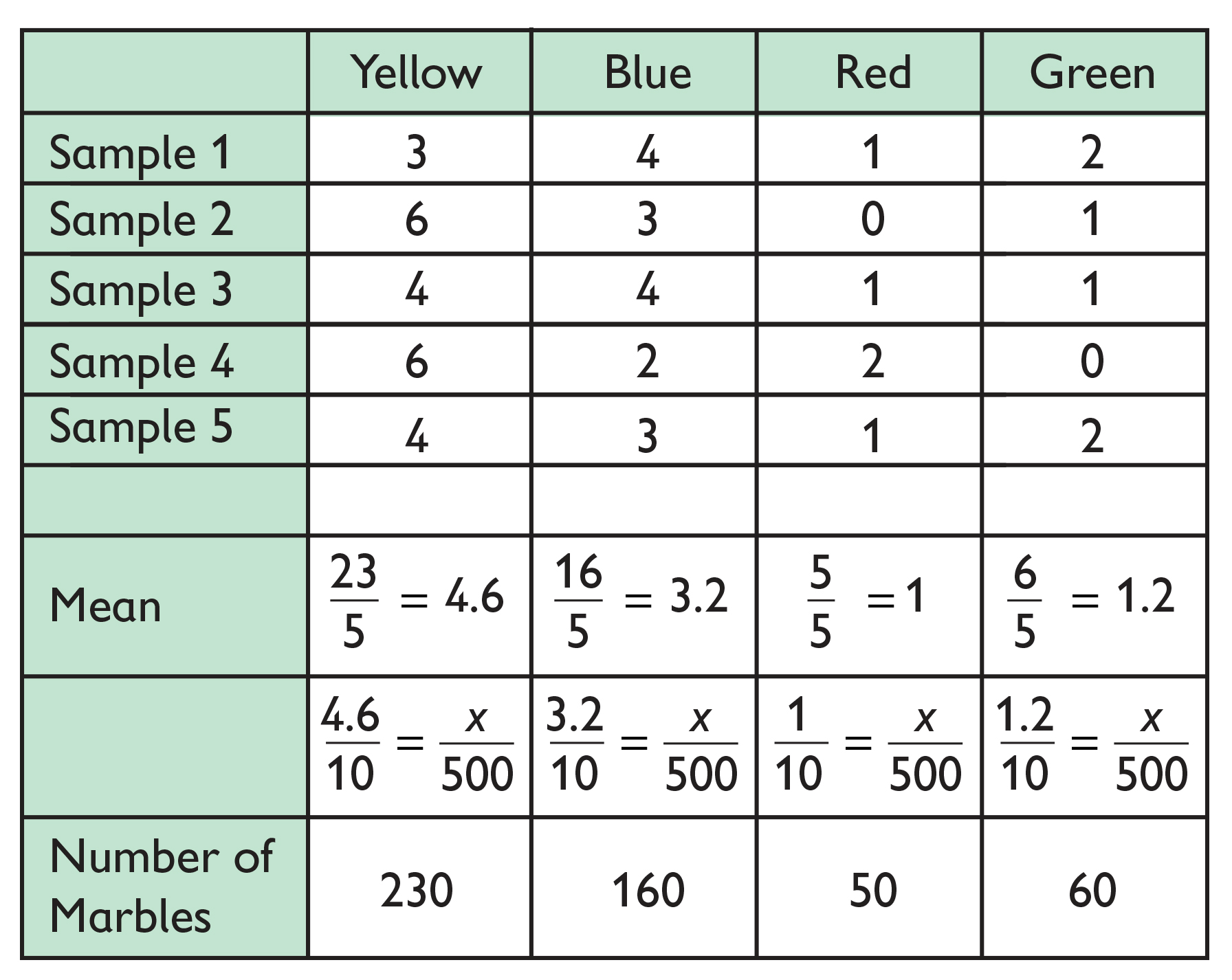
- 5 samples of 10 marbles:
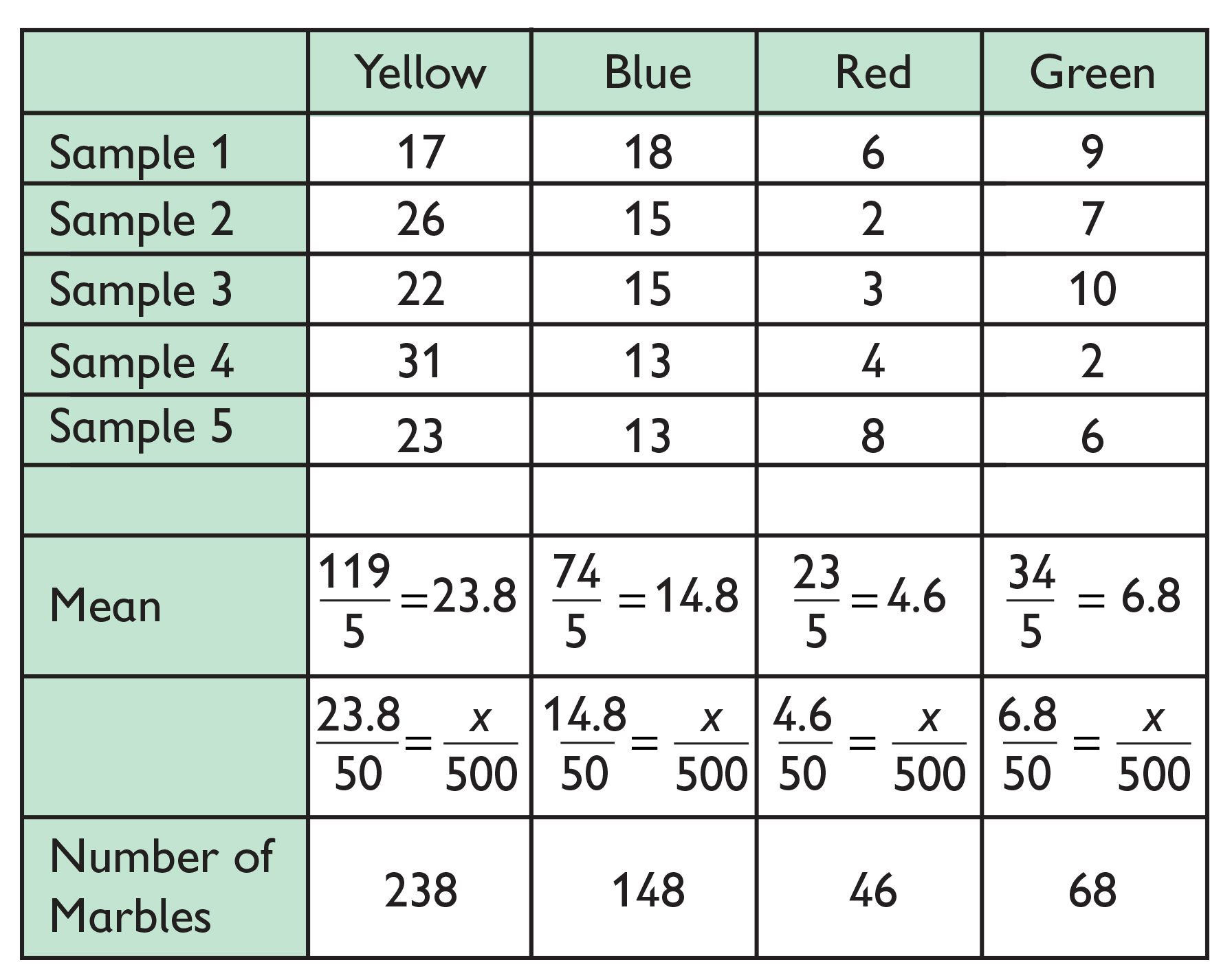
- 5 samples of 50 marbles:
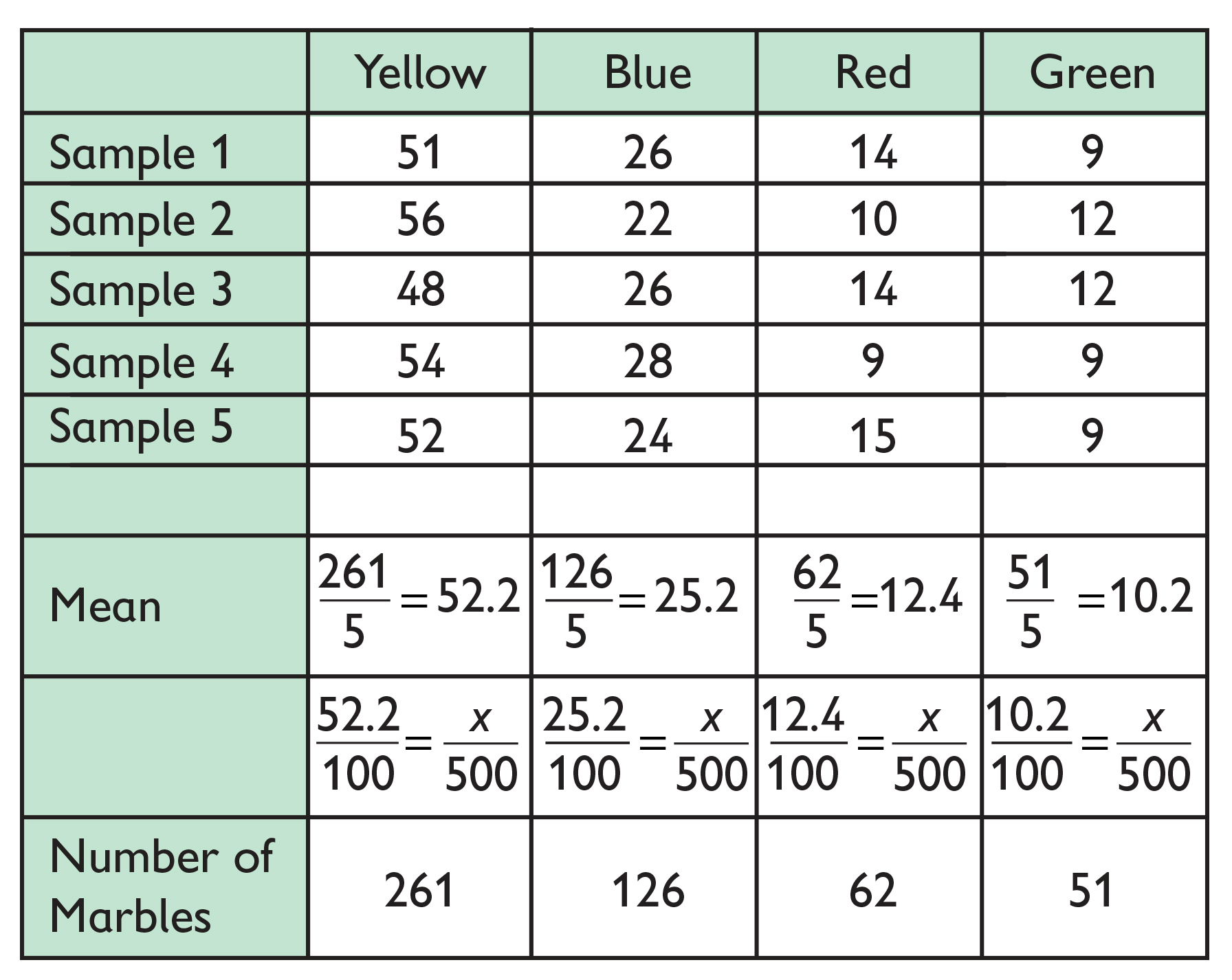
- 5 samples of 100 marbles:
Work Time
How Many Marbles?
You will take samples from the jar as specified below. The Marble Jar interactive will create samples that represents the glass jar of marbles from the Opening. Between each sample, all marbles will be replaced in the jar before the next sample is selected.
Do the following:
- For each group of five samples of different sizes, find the mean number of marbles for each color.
- Determine the number of marbles for each color in the jar, based on the mean you calculated for each color.
Samples:
- Draw 5 samples of 10 marbles each.
- Draw 5 samples of 50 marbles each.
- Draw 5 samples of 100 marbles each.
Hint:
- Remember, the mean is the average of the data set.
Prepare a Presentation
Lesson Guide
Possible responses that students will give to questions:
- For the samples of 10 marbles, the results are very different from each other (i.e., an individual sample deviates significantly from the mean). The results for the samples of 50 and 100 marbles are more similar to each other. This implies that the larger sample sizes more accurately represent the entire population of marbles.
- The results for the samples of 50 and 100 are more similar to each other than they are to the results of the samples of 10.
- Samples should be sufficiently large enough that student responses are close to the actual proportion of marbles in the jar: yellow (250), blue (125), red (60), green (65).
Record students' guesses for the number of marbles for each color for the marble jar with 500 marbles. Use your students' guesses to make a histogram. Show this histogram to your students in task 5.
Challenge Problem
Answers
- Answers will vary. Possible answer: The best sample size would be the largest (100 marbles). Because there is a lot of variety, you need to draw a lot of marbles to get an accurate measure of the number of each color marble.
Work Time
Prepare a Presentation
Think about these questions as part of your presentation.
- Within each sample size group, how do your results compare for the five samples? What does this comparison tell you?
- How do your results compare for the three sample size groups?
- How many marbles of each color do you think there are in the jar?
Challenge Problem
- If the jar held 500 marbles but had 10 different colors of marbles, what do you think the best sample size would be?
INTERACTIVE: Marble Jar
Make Connections
Lesson Guide
Have students present their observations. Have the class histograms ready to share.
If any students did the Challenge Problem, ask them to share their answers.
ELL: As ELLs explain their reasons verbally and in writing, their answers may have language errors. Remember, language mistakes are natural.
- Focus on the content being communicated
- Allow processing time
- Do not emphasize grammar
- Model standard English
SWD: Students with disabilities may struggle to follow the discussion and concurrently take notes during the Ways of Thinking portion of the lesson. Create scaffolded notes/questions based on the responses for some students. Use as reference and support during the Ways of Thinking portion of the lesson.
Mathematics
Questions to ask during discussion:
- Could the results of different samples have been added together to make one big sample? Why or why not?
- How did your predictions for the number of each color marble change as the sample size increased?
- How did the samples compare to each other within each sample size group?
- What do you think is the best sample size?
Discuss the utility of drawing 5 samples of 100 marbles each. Since the total population is 500 marbles, it would take just as much effort to count every single marble.
Lastly, reveal the number of each colored marble in the jar.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Since students are conducting experiments, there will be variability in the results. Students must be able to reason and defend their analysis and conclusions, even if they are different from others.
Performance Task
Ways of Thinking: Make Connections
Take notes about the approaches your classmates used to determine the number of each color of marble in the jar.
As your classmates present, ask questions such as:
- How do your results compare for the five samples within each sample size group?
- How do your results change as the sample size increases?
- How are the numbers of each color marble related to each other, if at all?
- Could the results of each sample within the same sample size group have been added together to make one big sample? Why or why not?
- Which sample size do you think is the best?
Samples and Sample Size
A Possible Summary
Sampling is a way to determine characteristics of a population. The sample size compared to the population is a large factor in the accuracy of results. If the sample is too small, the results will not represent the population. If the sample is too large, it defeats the purpose of sampling.
Formative Assessment
Summary of the Math: Samples and Sample Size
Write a summary about making conclusions about populations based on samples and the affect of sample size.
Check your summary:
- Do you discuss how you can determine characteristics of a population based on samples?
- Do you explain how sample size affects the conclusions you make about the population?
Reflect on Your Work
Lesson Guide
Have students write a brief reflection before the end of the class. Review the reflections to find out what connections students made between probability and sampling.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
When I think about probability and sampling, I see these connections...