- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Text/HTML
Balance Scale B
Balance Scale B
Balance Scale C
Balancing the Scale
Equal To, Greater Than, or Less Than?
Symbolic Representation

Overview
Lesson Overview
Students use weights to represent equal and unequal situations on a balance scale and represent them symbolically.
Key Concepts
- An equation is a statement that shows that two expressions are equivalent. An equal sign (=) is used between the two expressions to indicate that they are equivalent. You can think of the two expressions as being “balanced.”
- An inequality is a statement that shows that two expressions are unequal. The symbols for “greater than” (>) and “less than” (<) are used to indicate which expression has the greater or lesser value. In an inequality, you can think of the two expressions as being “unbalanced.”
Goals and Learning Objectives
- Explore a balance scale as a model for equations and inequalities.
- Understand that an equation states that two expressions are equivalent using an equal sign (=).
- Understand that an inequality states that one expression is greater than (>) or is less than (<) another expression.
- Use the equal sign (=) and the greater than (>) and less than (<) symbols with rational numbers.
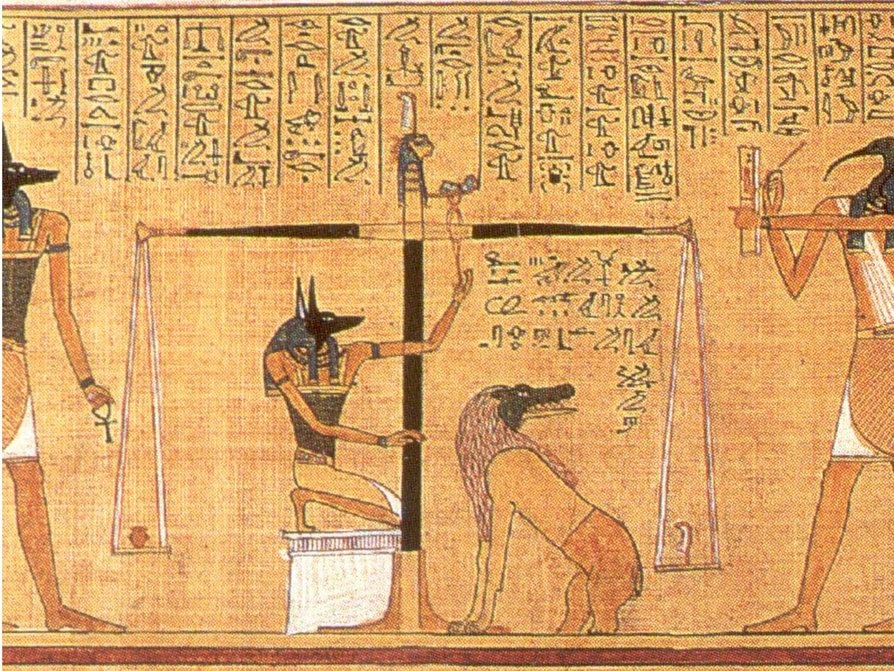
History of Scales
Lesson Guide
Have students read the text about the history of the balance scale and discuss what they know about scales with their partner.
Opening
History of Scales
The history of balance scales begins in ancient Egypt, possibly as far back as 5000 BCE. The Egyptians used balance scales to compare the weights of goods. They placed goods on each side of the scale; when the scale became balanced, they knew that the weights of the goods were equal.
- What type of scales have you used, or seen someone else use, to measure things?
- How are the scales you've used similar to, or different from, the balance scale?
Hint:
- Think about places you visit, like the grocery store or the doctor's office. Have you seen scales there?
- Scales are used to measure weight. What are some of the things we weigh?
Balancing the Scale
Lesson Guide
Have students look at the Balancing the Scale interactive. Demonstrate how to put 2 and 3 on the left side of the scale.
Ask students: What number(s) do you need to place on the right side of the scale in order to balance the scale? Have students turn and talk to their partners about the question, and then try to balance the scale. After a few minutes, have students share and discuss their findings with the class. When several responses have been verbalized, discuss the definition of equation. Then ask students to represent the balance scale using an equation.
Ask students: How can you make the scale unbalanced so that the left side is heavier than the right side? Have students unbalance the scale and share what they did. Then discuss the definition of inequality. Ask students to represent the unbalanced scale using an inequality.
Possible Answers
- 5; 4 and 1; or 2 and 3
- 2 + 3 = 5; 2 + 3 = 4 + 1; or 2 + 3 = 2 + 3
- Answers will vary.
- Possible answer: 2 + 3 > 3
Opening
Balance Scales
An equation consists of two equivalent expressions that are linked by an equal sign (=).
An inequality consists of two nonequivalent expressions that are linked by a less than sign (<) or a greater than sign (>).
Using the Balance Scale interactive, place the numbers 2 and 3 on the left side of the scale.
- What number(s) do you need to place on the right side of the scale in order to balance the scale?
- Write an equation to represent the balanced scale.
- Now, “unbalance” the scale so that what is on the left side is greater than what is on the right side.
- Write an inequality to represent the unbalanced scale.
INTERACTIVE: Balancing the Scale
Hint:
- Think about the definitions of equation andinequality :
- An equation consists of two equivalent expressions that are linked by an equal sign (=).
- An inequality consists of two nonequivalent expressions that are linked by a less than sign (<) or a greater than sign (>).
Math Mission
Lesson Guide
Discuss the Math Mission. Students will set up balanced and unbalanced scales and represent the scales using equations and inequalities.
Opening
Set up balanced and unbalanced scales, and represent the scales using equations and inequalities.
Equations and Inequalities
Lesson Guide
Have students work in pairs on these problems.
ELL: For this task, encourage students to explain their ideas to one another. Math language must be used. Encourage the use of English without discouraging students from using their primary language.
Mathematical Practices
Mathematical Practice 7: Look for and make use of structure.
Look for students who have ideas that help them relate the equal sign (=) and the inequality symbols (< and >) to the tilt of the scale.
Interventions
Student does not understand the task.
- Reread the instructions. Ask your partner for help.
- What does a balanced scale look like?
- What does an unbalanced scale look like?
Student does not know how to write an equation or an inequality to represent the scale.
- What is the value of the left side of the scale? The right side?
- Is the scale balanced or unbalanced?
- What sign can you use to represent a balanced scale?
- What symbols can you use to represent an unbalanced scale?
- What does the < symbol mean?
- What does the > symbol mean?
Student has a solution.
- Explain your strategy for setting up the balance scale.
- Explain how your equation [inequality] represents your balance scale.
SWDL Check for understanding by asking students to restate new terms or concepts in their own words, as well as any directions they will need to follow during the lesson. Students should be able to explain the relationship between a balanced equation and an unbalanced inequality.
Possible Answers
- Answers will vary. A balanced scale that has two numbers on each side, using four different numbers: 1 + 5 = 2 + 4
- A modified scale from the previous step with the right side less than the left side: 1 + 5 > 1 + 4
- An unbalanced scale with one number on one side and two numbers on the other side: 6 > 2 + 1
- A modified scale from the previous step that is balanced: 6 = 5 + 1
- An unbalanced scale that has three numbers on one side and two numbers on the other side, such that the side with the two numbers is greater than the side with the three numbers: 1 + 2 + 3 < 4 + 5
- A modified scale from the previous step that is balanced: 1 + 2 + 3 = 1 + 5
- A modified scale from the previous step that has the same number added on each side: 1 + 2 + 3 + 4 = 1 + 5 + 4. The scale remains balanced after placing the same number on each side.
Work Time
Equations and Inequalities
Set up numbers on both sides of the scale to match the descriptions below.
After you set up each scale, write the equation or inequality that represents the scale.
- Use Balance Scale A to set up a balanced scale (both sides equal) that has two numbers on both sides, using four different numbers.
- Modify your scale from the previous step to make the right side less than the left side.
- Use Balance Scale B to set up an unbalanced scale with one number on one side and two numbers on the other side.
- Modify your scale from the previous step to make it balanced.
- Use Balance Scale C to set up an unbalanced scale that has three numbers on one side and two numbers on the other side, such that the side with two numbers is greater than the side with the three numbers.
- Modify your scale from the previous step to make it balanced.
- Modify your scale again by placing the same number on both sides. What happens?
INTERACTIVE: Balance Scale A
INTERACTIVE: Balance Scale B
INTERACTIVE: Balance Scale C
Hint:
- Think about the definitions of equation andinequality :
- An equation consists of two equivalent expressions that are linked by an equal sign (=).
- An inequality consists of two nonequivalent expressions that are linked by a less than sign (<) or a greater than sign (>).
- If the scale is balanced, write an equation.
- If the scale is not balanced, write an inequality.
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who understand that a balanced scale can be represented with an equation and an unbalanced scale can be represented with an inequality statement. Identify different solutions to share in the Ways of Thinking discussion. Make note of students who are having trouble so you can address any misconceptions in the Ways of Thinking discussion.
Answers
- Presentations will vary.
Challenge Problem
The Challenge Problem reuses the interactive Balance Scale B. Instruct students to ignore the directions in the interactive, and to use the scale to complete the directions given in the Challenge Problem.
Answer
- No, if you add the same amount to each side of an unbalanced scale, the scale will remain unbalanced.
Work Time
Prepare a Presentation
- Choose one equation or inequality that you created in the Balance Scale interactives that you think is particularly interesting.
- Use this equation/inequality to explain your understanding of equations and/or inequalities. In your explanation, refer to the corresponding scale you created using the interactive.
Challenge Problem
NOTE: Ignore the instructions in the interactive and follow the steps below.
- Place a number on the left side of the scale.
- Place a different number on the right side.
- Is there any one number you can now add on both sides that will balance the scale? Explain.
INTERACTIVE: Balance Scale B
Hint:
- Think about the definitions of equation andinequality :
- An equation consists of two equivalent expressions that are linked by an equal sign.
- An inequality consists of two nonequivalent expressions that are linked by a less than sign (<) or a greater than sign (>).
Make Connections
Lesson Guide
Have students share their presentations. Review the following points as students share their work:
- Point out different ways students set up a balanced scale that has two numbers on each side, using four different numbers. Ask students why each representation of the scale uses an equation.
- Discuss the different ways students modified the scale to make the right side less than the left side. Some students may have added to the left side, while others may have taken away from the right side. Compare the different inequality statements that represent these approaches. Why do they all use the > symbol?
- Look for different ways of setting up an unbalanced scale with one number on one side and two numbers on the other side. Some students may have the one number greater than the two numbers; other students may have the one number less than the two numbers. Discuss the different inequality statements and how they represent the unbalanced scales. Have students who have devised a way of knowing which inequality symbol to use share their strategies.
- Then discuss how to make an unbalanced scale balanced. What do you need to do to make a scale balanced? Students may have added to one side or taken away from a side. Compare the different representations of the balanced scale. What is similar? (They all use an equal sign.)
- Then have students compare different strategies for finding two numbers that are greater than three numbers and how the unbalanced scale is represented using an inequality statement.
- Be sure at the end of the discussion that students understand the meanings of equation and inequality and how they are modeled using a scale.
Have students who completed the Challenge Problem explain why it is impossible to add the same number to each side of an unbalanced scale to balance the scale. Demonstrate using the Balance Scale B interactive.
ELL: When selecting a group of students to present in the Ways of Thinking section, ensure students present a topic they are confident about. Have students draw diagrams or demonstrate their knowledge in some other way than through verbal language alone.
Performance Task
Ways of Thinking: Make Connections
Take notes as your classmates explain their understanding of equations and inequalities.
Hint:
As your classmates present, ask questions such as:
- Should the pointed side of the inequality sign point to the greater or lesser number?
- How does the equation or inequality you wrote represent the balance scale you made?
- What can you do to an unbalanced scale to balance it? How can you represent the balanced scale using an equation or an inequality?
- What can you do to a balanced scale to make the right side greater than the left side? How can you represent this scale using an equation or an inequality?
Equal to, Greater Than, or Less Than?
Lesson Guide
As students complete these problems, look for students who may be struggling with fraction and decimal concepts, operations, or negative numbers. Pair those students with students who have been successful with these concepts.
SWD: Students with disabilities may have difficulty working with decimals and fractions, especially when applying decimals and fractions to inequalities. If students demonstrate difficulty to the point of frustration, provide direct instruction on the basics for adding decimals and fractions.
Mathematics
As you go over the answers to these problems, encourage students who used mathematical reasoning, properties, or estimation to share their thinking processes.
For example:
- For 5 + 7 ☐ 8 + 12, I saw immediately that 5 + 7 was 12, so 8 + 12 must be greater. Therefore, 5 + 7 < 8 + 12.
- For , I knew that if a whole were divided into 3 pieces, each piece would be greater than if that whole were divided into 5 pieces. Therefore, .
- For 5.4 + 2.06 ☐ 8 + 0.3, I knew the left side was less than 8, so it had to be less than the right side. Therefore, 5.4 + 2.06 < 8 + 0.3.
- For 9.8 + 6.7 + 0.4 ☐ 6.7 + 9.8 + 0.4, I knew that the two expressions were equal because of the commutative property of addition. Therefore, 9.8 + 6.7 + 0.4 = 6.7 + 9.8 + 0.4.
- For , I knew that , and I knew was greater than . Therefore,
Answers
a. =
b. <
c. >
d. <
e. =
f. <
g. =
h. <
i. <
j. >
Work Time
Equal to, Greater Than, or Less Than?
- Place =, >, or < in the boxes in the equations and inequalities.
INTERACTIVE: Equal to, Greater Than, or Less Than?
Equations and Inequalities
A Possible Summary
A statement that shows that two expressions are equal to one another is an equation. You can use an equal sign (=) to show that the expressions are equal. A statement that shows that two expressions are unequal is an inequality statement; an inequality statement specifies which expression has the greater value (or lesser value). You can use the less than (<) or greater than (>) symbols to show which expression is less than or greater than the other.
Formative Assessment
Summary of the Math: Equations and Inequalities
Write a summary about equations and inequalities based on what you learned today.
Hint:
Check your summary:
- Do you explain the difference between an equation and an inequality?
- Do you explain the meaning of the signs <, >, and =?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to learn if students understand how equations and inequalities can be represented using a balance scale.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
A balance scale helps me understand equations and inequalities because …