- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Problem Solving Exercise

Overview
Lesson Overview
Students practice solving equations using either the addition or the multiplication property of equality.
Key Concepts
Students will solve equations of the form x + p = q using the addition property of equality.
They will solve equations of the form px = q using the multiplication property of equality.
They will need to look at the variable and decide what operation must be performed on both sides of the equation in order to isolate the variable on one side of the equation.
If a number has been added to the variable, they will subtract that number from both sides of the equation. If a number has been subtracted from the variable, they will add that number to both sides of the equation. If the variable has been multiplied by a number, students will either divide both sides of the equation by that number or multiply by the reciprocal of that number. If the variable has been divided by a number, students will multiply by that number. Students will see how this can be applied to solving a proportion such as .
Goals and Learning Objectives
- Practice solving equations using either the addition or the multiplication property of equality.
- Distinguish between equations that can be solved using the addition property of equality from equations that can be solved using the multiplication property of equality.
- Solve a proportion by solving an equation.
Which Property Do I Use?
Lesson Guide
Have students work in pairs to identify the property they can use to solve each equation.
ELL: When monitoring students, pay special attention to ELLs to ascertain that they are on task and clear about what needs to be done. Provide enough time for students to discuss which properties they used and why.
SWD: This lesson is a review and application of skills learned so far in this unit. Consider the prerequisite skills for this lesson. Students with disabilities may need review, direct instruction, and guided practice with the skills needed to complete the tasks that follow. Make sure all students understand the terms included in this lesson. Students should understand these domain-specific terms:
- addition property of equality
- multiplication property of equality
- proportion
Re-teach/review these terms to students with disabilities.
Mathematics
After pairs have made their matches, have students describe how they decided which property to use. Students should explain that they looked to see what operation was performed already on the variable. If an amount has been added to or subtracted from the variable, they use the addition property of equality. If the variable has been multiplied or divided by some number, they use the multiplication property of equality.
Opening
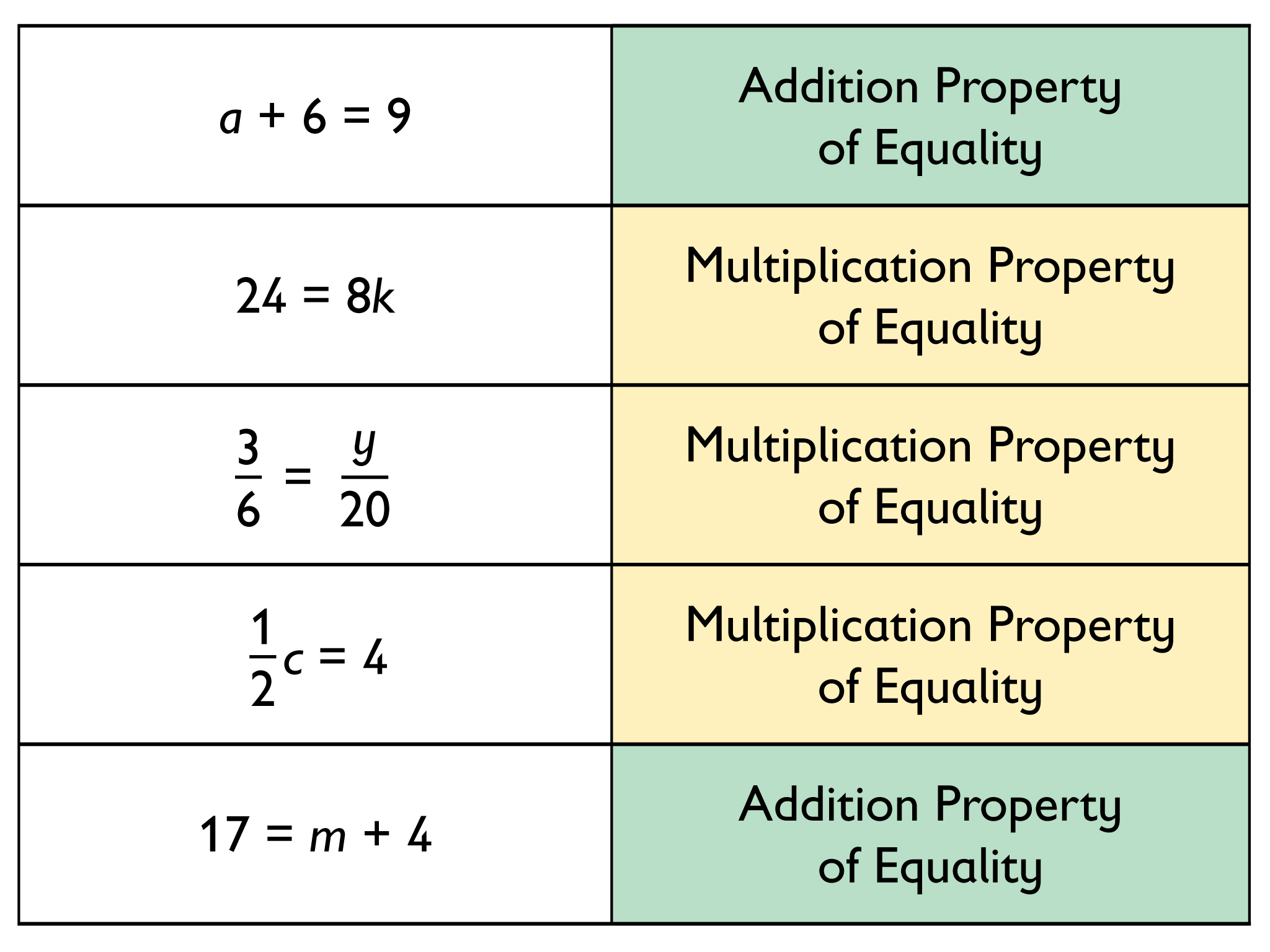
Which Property Do I Use?
- Sort each equation into one of these two categories:
- Equations you can solve using the addition property of equality
- Equations you can solve using the multiplication property of equality
HANDOUT: Which Property Do I Use?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will solve equations using either the addition property of equality or the multiplication property of equality.
Opening
Solve equations using either the addition property of equality or the multiplication property of equality.
An Equation with Decimals
Lesson Guide
Have students work in pairs on all problems in Tasks 3, 4, 5, and 6.
SWD: Students with disabilities may use an incorrect property. Ask students to read the equation to you to see if they correct the misconception. Pay special attention to how they read their equation.
ELL: When discussing this example, make a point of writing the questions on the board, along with students' responses. This will assist ELLs by giving them written and oral access to the questions. Make sure students record important information in their Notebook.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who check their work using substitution and revise accordingly.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who make errors so that these can be discussed during Ways of Thinking.
Mathematical Practice 6: Attend to precision.
Look for students who correctly record the steps for solving the equations and correctly identify the properties they are using.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who see that the overall goal in solving each equation is the same—isolate the variable—even when the operation used to do so differs.
Interventions
Student uses the wrong operation when trying to isolate the variable.
- What operation has been applied to the variable now?
- What is the opposite of that operation?
- How do you undo addition (multiplication)?
Student is unable to identify the sides of the equation because the variable is on the right.
- What is the equal sign?
- Now tell me what is on the left side of the equal sign.
- Now tell me what is on the right side of the equal sign.
Student gets the wrong answer.
- Write the equation you are trying to solve.
- Substitute your solution for the variable. Do you get a true equation?
- Try solving the equation again.
Answers
- 8.05 = x + 4.9
8.05 – 4.9 = x + 4.9 – 4.9 Addition property of equality
x = 3.15
Check:
8.05 = 3.15 + 4.9
80.5 = 8.05
Work Time
An Equation With Decimals
- Use either the addition or multiplication property of equality to solve this equation:
8.05 = x + 4.9 - Write the name of the property, and show each step you used to find the solution.
- Check your solution by substituting it for x in the equation. Does your solution make the equation true?
Hint:
- Try to get x by itself on one side of the equation.
- If substituting your solution does not result in a true equation, go back and check the steps you used to find your solution.
An Equation With Whole Numbers
Lesson Guide
Have students work in pairs on all problems in Tasks 3, 4, 5, and 6.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who check their work using substitution and revise accordingly.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who make errors so that these can be discussed during Ways of Thinking.
Mathematical Practice 6: Attend to precision.
Look for students who correctly record the steps for solving the equations and correctly identify the properties they are using.
Mathematical Practice 7: Look for and make use of structure.
Look for students who use division and for students who multiply by the reciprocal.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who see that the overall goal in solving each equation is the same—isolate the variable—even when the operation used to do so differs.
Interventions
Student uses the wrong operation when trying to isolate the variable.
- What operation has been applied to the variable now?
- What is the opposite of that operation?
- How do you undo addition (multiplication)?
Student does not understand why you can use multiplication or division.
- Dividing by 7 gives the same result as multiplying by ….
Student gets the wrong answer.
- Write the equation you are trying to solve.
- Substitute your solution for the variable. Do you get a true equation?
- Try solving the equation again.
Answers
- 7y = 329
= Multiplcation property of equality
y = 47
Check:
7 • 47 = 329
329 = 329
Work Time
An Equation With Whole Numbers
- Use either the addition or multiplication property of equality to solve this equation:
7y = 329 - Write the name of the property, and show each step you used to find the solution.
- Check your solution by substituting it for y in the equation. Does your solution make the equation true?
Hint:
- Think about what operation you will use, and whether you will use a whole number or a fraction with that operation.
- If substituting your solution does not result in a true equation, go back and check the steps you used to find your solution.
An Equation With a Fraction
Lesson Guide
Have students work in pairs on all problems in Tasks 3, 4, 5, and 6.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who check their work using substitution and revise accordingly.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who make errors so that these can be discussed during Ways of Thinking.
Mathematical Practice 6: Attend to precision.
Look for students who correctly record the steps for solving the equations and correctly identify the properties they are using.
Mathematical Practice 7: Look for and make use of structure.
Look for students who use division and for students who multiply by the reciprocal.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who see that the overall goal in solving each equation is the same—isolate the variable—even when the operation used to do so differs.
Interventions
Student uses the wrong operation when trying to isolate the variable.
- What operation has been applied to the variable now?
- What is the opposite of that operation?
- How do you undo addition (multiplication)?
Student does not understand why you can use multiplication or division.
- Dividing by gives the same result as multiplying by ….
Student gets the wrong answer.
- Write the equation you are trying to solve.
- Substitute your solution for the variable. Do you get a true equation?
- Try solving the equation again.
Answers
- m = 12
• m = • 12 Multiplication property of equality
m = 18
Check:
• 18 = 12
12 = 12
Work Time
An Equation With a Fraction
- Use either the addition or multiplication property of equality to solve this equation:
m = 12 - Write the name of the property, and show each step you used to find the solution.
- Check your solution by substituting it for m in the equation. Does your solution make the equation true?
Hint:
- Think about what operation you will use, and whether you will use a whole number or a fraction with that operation.
- If substituting your solution does not result in a true equation, go back and check the steps you used to find your solution.
A Proportional Equation
Lesson Guide
Have students work in pairs on all problems in Tasks 3, 4, 5, and 6.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who check their work using substitution and revise accordingly.
Mathematical Practice 2: Reason abstractly and quantitatively.
Look for students who check their answer to by solving the proportion in a different way.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who make errors so that these can be discussed during Ways of Thinking.
Mathematical Practice 6: Attend to precision.
Look for students who correctly record the steps for solving the equations and correctly identify the properties they are using.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who see that the overall goal in solving each equation is the same—isolate the variable—even when the operation used to do so differs.
Interventions
Student uses the wrong operation when trying to isolate the variable.
- What operation has been applied to the variable now?
- What is the opposite of that operation?
- How do you undo addition (multiplication)?
Student gets the wrong answer.
- Write the equation you are trying to solve.
- Substitute your solution for the variable. Do you get a true equation?
- Try solving the equation again.
Answers
• 7 = • 7 Multiplication property of equality
p =
p = 21
Check:
=
3 = 3
Work Time
A Proportional Equation
- Use either the addition or multiplication property of equality to solve this equation:
- Write the name of the property, and show each step you used to find the solution.
- Check your solution by substituting it for p in the equation. Does your solution make the equation true?
Hint:
Which property would you use to get p by itself on one side of the equation?
Prepare a Presentation
Preparing for Ways of Thinking
Look for students who have different solution methods to share in the Ways of Thinking discussion.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for students who check their work using substitution and revise accordingly.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Look for students who make errors so that these can be discussed during Ways of Thinking.
Mathematical Practice 6: Attend to precision.
Look for students who correctly record the steps for solving the equations and correctly identify the properties they are using.
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
Look for students who see that the overall goal in solving each equation is the same—isolate the variable—even when the operation used to do so differs.
Challenge Problem
Answer
- 5x + 2 = 2x + 9
5x – 2x + 2 = 2x – 2x + 9 Addition property of equality
3x + 2 = 9
3x + 2 – 2 = 9 – 2 Addition property of equality
3x = 7
= Multiplicaton property of equality
x = 2
Work Time
Prepare a Presentation
Choose one of the equations you solved to present.
- Show the steps you took to solve the equation.
- Explain how you used one of the properties of equality to solve.
Challenge Problem
- How could you use the addition and multiplication properties of equality to solve the equation 5x + 2 = 2x + 9?
Make Connections
Lesson Guide
- As you discuss the Work Time problems, be sure to include students who may have misconceptions so that you can engage the class in active discussion.
- For 7y = 329 and m = 12, try to include both students who used multiplication and students who used division.
- Look for students who use precise vocabulary in describing the steps they used to solve an equation and in naming the properties used.
- If possible, allow a student with an incorrect solution to show what happens when the incorrect solution is substituted into the equation. The resulting equation will be false.
- If students have incorrect solutions due to their not understanding fraction or decimal operations, include a discussion of those incorrect solutions as well. There may be other students who could benefit from a review of these operations.
- For the proportion , take this opportunity to allow students to demonstrate alternative ways to solve the proportion. For example, a student might use the ratio to determine the unit rate: 3 to 1. The student can then reason that would represent that same unit rate, and so 21 must be the solution to the proportion.
If any students attempted the Challenge Problem, have them share their solutions. If the solutions are incorrect, have the class work together to find the correct solution. If no one attempted the problem, provide the first step: Subtract 2x from both sides. Then allow students to attempt the rest of the solution.
SWD: On a chart, write the key points that students make during their presentations of problems from Tasks 3, 4, 5, 6.
Performance Task
Ways of Thinking: Make Connections
- Take notes about the properties and steps your classmates used to solve the equations.
Hint:
As your classmates present, ask questions such as:
- How did you know which property to use?
- Why do you get the same result whether you multiply by or divide by 7?
- You divided by . Could you multiply by instead?
Properties of Equality
Lesson Guide
- Have pairs quietly discuss the information about the properties of equality. Have them give examples of how to use the properties to solve equations.
- As student pairs work together, listen for students who may still have misconceptions so that you can address them in the class discussion.
- After a few minutes, discuss the Summary as a class. Review the following points:
- If a number has been added to (subtracted from) a variable in an equation, that number will need to be subtracted from (added to) both sides of the equation to solve it. This process makes use of the addition property of equality. It can be used to solve equations such as x + 4 = 10 and x − 2 = 12.
- If a variable has been multiplied by a number, both sides of the equation will need to be divided by that number to solve it. This process makes use of the multiplication property of equality. It can be used to solve equations such as 4x = 12.
- If a variable has been divided by a number, both sides of the equation will need to be multiplied by that number to solve it. This process makes use of the multiplication property of equality. It can be used to solve equations such as = 12 and can also be used to solve proportions such as .
- Dividing by a number gives the same result as multiplying by the reciprocal of that number. So, when using the multiplication property of equality, you can use either operation. To solve 7x = 56, you can divide both sides of the equation by 7 or you can multiply both sides by . The result is the same. Similarly, you can solve x = 6 by either multiplying by or dividing by .
Formative Assessment
Summary of the Math: Properties of Equality
Read and Discuss
- Addition property of equality : If a = b, then a + c = b + c.
- Multiplication property of equality : If a = b, then ac = bc.
- These two properties of equality are very useful. For any equation that is true, you can
- Add the same value to both sides or subtract the same value from both sides and the equation will still be true.
- Multiply or divide both sides by the same value and the equation will still be true.
Hint:
Can you:
- Provide examples of equations that can be solved using the addition property of equality, and explain the steps for using the property to solve each equation?
- Provide examples of equations that can be solved using the multiplication property of equality, and explain the steps for using the property to solve each equation?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to see whether students understand how to use properties to solve equations.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starters below if you find them to be helpful.
I can use the addition property of equality when …
I can use the multiplication property of equality when …