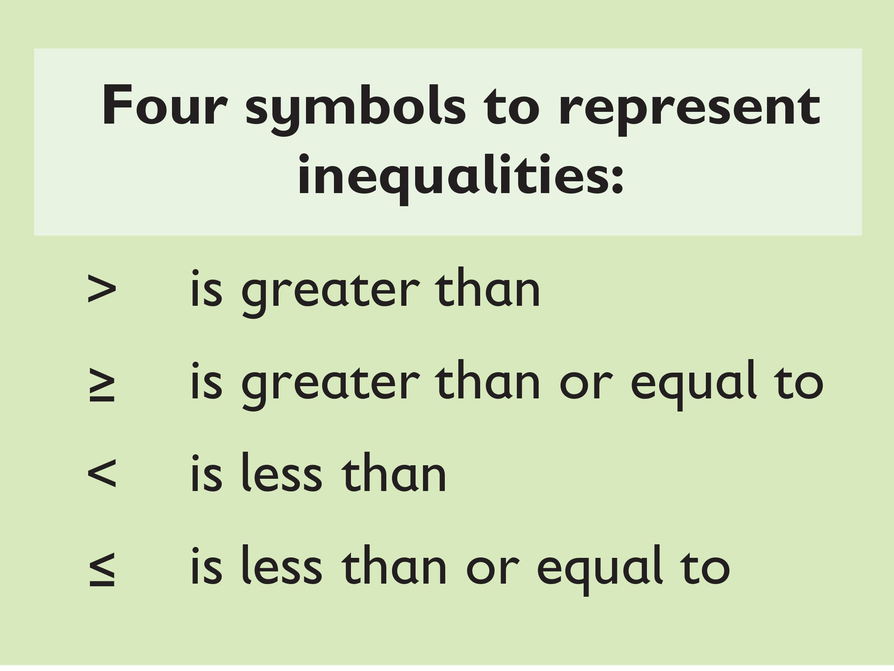Inequality Statements Including Variables

Overview
Lesson Overview
Students represent real-world situations using inequality statements that include a variable.
Key Concepts
Inequality statements tell you whether values in a situation are greater than or less than a given number and also tell you whether values in the situation can be equal to that number or not.
The symbols < and > tell you that the unknown value(s) in a situation cannot be equal to a given number: the unknown value(s) are strictly greater than or less than the number. The inequality x < y means x must be less than y. The inequality x > y means x must be greater than y.
The symbols ≤ and ≥ tell you that the unknown value(s) in a situation can also be equal to a given number: the unknown value(s) are less than or equal to, or greater than or equal to, the number. The inequality x ≤ y means x is less than or equal to y. The inequality x ≥ y means x is greater than or equal to y.
Goals and Learning Objectives
- Understand the inequality symbols <, >, ≤, and ≥.
- Write inequality statements for real-world situations.
ELL: When writing the summary, provide ELLs access to a dictionary and give them time to discuss their summary with a partner before writing, to help them organize their thoughts. Allow ELLs who share the same primary language to discuss in their native language if they wish.
Swimming Class
Lesson Guide
Have students work in pairs on the task.
Mathematics
- Students should conclude that 10 or fewer means that there can be 5 or 10 students, but not 12 students. Be sure students understand that 10 is a possibility.
- The challenge will be how to write the inequality to represent the possible ages. Most students may not be familiar with the symbol ≤, so they may create other ways to write the inequality. Allow all students to share their ideas before presenting the answer, n ≤ 10.
Opening
Swimming Class
The size of a swimming class is limited to 10 or fewer students.
- Talk with a partner. Can the swimming class have 5 students? 12 students? Exactly 10 students?
- Let n represent the number of students who can participate in the swimming class. How can you write an inequality to represent this situation?
Math Mission
Lesson Guide
Discuss the Math Mission. Students will write and interpret inequalities.
Opening
Write and interpret inequalities.
Write and Interpret Inequalities
Lesson Guide
Have students work in pairs on the problems.
ELL: When forming partnerships, consider the task at hand. Since the task is language heavy, pair ELLs with native speakers who can help them understand the question.
SWD: Point to or highlight the key parts of the word problem so that students can ascertain why that particular inequality sign was used.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Look for students who struggle with, as well as those who are at ease with, interpreting the descriptions in the problems that require the ≤ and ≥ symbols in order to model them effectively.
Mathematical Practice 2: Reason abstractly and quantitatively.
Identify students who consider the reasonableness of the types of numbers given for each of the contexts when identifying values for the first problem. For example:
- Using only whole numbers for the number of points scored in the game
- Using monetary values for what you can spend on a movie and popcorn
- Including negative values for temperature
Interventions
Student does not understand the task.
- Describe the task in your own words to your partner.
- What are you trying to write?
- Can you use x in an inequality statement to represent the situation?
Student struggles with translating from words to mathematical representations.
- Read the descriptions aloud.
- Try saying an inequality statement aloud before attempting to write it.
- Use a letter to represent the quantity that is being described. Then use this letter in an inequality statement to show that the quantity must be greater than or less than the amount in the description.
Student finishes quickly and easily.
- Try the Challenge Problem. What types of numbers make sense in the given situations?
Answers
- h ≥ 54
h = 54, 54, or 60 inches
- m + p ≤ 8 or x ≤ 8
m = $5.00 and p = $2.00; or x = $7.00
m = $5.75 and p = $2.25; or x = $8.00
m = $4.00 and p = $3.95; or x = $7.95
- x ≥ 30
x = 30, 31, or 40 years old
- t ≤ 32
t = 32°F, 0.5°F, or –10°F
- x > 300
x = 301, 400, or 500 points
Work Time
Write and Interpret Inequalities
Represent each situation below with an inequality that includes a variable.
For each situation, give three numbers that solve the inequality.
- To ride the roller coaster, a rider must be at least 54 inches tall. (Use h to represent the height in inches of a rider.)
- The most you can spend on a movie and popcorn is $8.00.
- To run for sheriff, you must be at least 30 years old.
- Water freezes at a temperature of 32°F or below.
- Martin scored more than 300 points in the game.
Hint:
- Roller coaster problem: Can the height (h) be equal to 54 when the problem says “at least” 54 inches?
- Movie problem: Let d represent the amount you can spend in dollars.
- Sheriff problem: Choose a variable to represent the age in years.
- Water temperature problem: Choose a variable to represent the temperature in degrees Fahrenheit.
- Game problem: Could Martin have scored exactly 300 points?
Is Mia’s Statement True?
Lesson Guide
Have students work in pairs on the problems.
ELL: When forming partnerships, consider the task at hand. Since the task is language heavy, pair ELLs with native speakers that can help them understand the question.
Mathematical Practices
Mathematical Practice 4: Model with mathematics.
Watch for students who use the number line effectively as a model for making sense of Mia's statement about 4 < x representing the same relationship as x > 4.
Interventions
Student finishes quickly and easily.
- Try the Challenge Problem. What types of numbers make sense in the given situations?
Possible Answers
- Yes, Mia is correct; 4 < x and x > 4 represent the same relationship. 4 < x means that 4 is less than x, and x > 4 means that x is greater than 4. Both of these mean that x is to the right of 4 on the number line.
Work Time
Is Mia's Statement True?
Mia says that 4 < x represents the same relationship as x > 4.
- Is her statement true? Explain why or why not.
Hint:
Try replacing x with a number.
Prepare a Presentation
Prepare for Ways of Thinking
As students are working, look for students who can use the inequality symbols correctly to represent the situations and those who cannot. In the Ways of Thinking discussion, you will want to discuss why the inequality statements match the situations and why the inequality statements do not match the situations.
Challenge Problem
Answers
- Inches of height are usually measured in positive whole numbers and fractions (64", 56", 61").
- Money is measured in decimals to the hundredths place. Positive numbers (money gained), negative numbers (money lost), and zero (no money) can all be used to describe money, but in this case they are referring to money you are going to spend, so it is positive ($2.75 or $8.00).
- Age is usually measured in positive whole numbers of years but may include fractions .
- Temperature is usually measured in integer numbers (including negative values and zero) but may include decimal numbers (32°, −11.5°, 0°).
- Points are usually measured in whole numbers, either positive or zero (350, 301, 417).
Work Time
Prepare a Presentation
Choose one of the scenarios and present the inequality you wrote for it.
- Explain how you used an inequality sign to show the relationship between two quantities.
- Support your explanation with your work.
Challenge Problem
For each of the inequality situations:
- Describe the types of numbers (for example, integers, decimals, positive and/or negative numbers) that fit the situation.
- Give an example of each type of number that could be a solution to the inequality.
- To ride the roller coaster, a rider must be at least 54 inches tall.
- The most you can spend on a movie and popcorn is $8.00.
- To run for sheriff you must be at least 30 years old.
- Water freezes at a temperature of 32°F or below.
- Martin scored more than 300 points in the game.
Make Connections
Lesson Guide
Discuss the different strategies students use to translate between verbal descriptions and the <, >, ≤, and ≥ symbols. In particular, have students present a variety of approaches to the movie and popcorn situation.
Ask students: What clues in the descriptions give information about the math of each situation?
The number line is an excellent tool for making sense of Mia's statement and may also help with reinforcing correct answers to situations.
Ask students: Are the possible values of the variable to the left or to the right of the given number? Can the value be equal to the given number or not?
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ representations and explanations of inequalities.
Hint:
As your classmates present, ask questions such as:
- How did you decide which inequality symbol to use?
- Why did you include 30 (in the inequality about age for running for sheriff)?
- Why didn't you include 300 (in the inequality about points that Martin scored)?
Inequalities
A Possible Summary
The inequality x < 4 means x must be less than 4. The inequality x > 4 means x must be greater than 4. The inequality x ≤ 4 means x is less than or equal to 4. The inequality x ≥ 4 means x is greater than or equal to 4.
Additional Discussion Points
- Inequality statements tell you whether values in a situation are greater than or less than a given number and also tell you whether values in the situation can be equal to that number or not.
- The symbols < and > tell you that the unknown value(s) in a situation cannot be equal to a given number: the unknown value(s) are strictly less than or greater than the number.
- The symbols ≤ and ≥ tell you that the unknown value(s) in a situation can also be equal to a given number: the unknown value(s) are less than or equal to, or greater than or equal to, the number.
ELL: When introducing new mathematical language, make sure you provide plenty of time for ELLs to process the newly acquired information. Provide an anchor chart with example word problems that use inequalities to represent situations.
Formative Assessment
Summary of the Math: Inequalities
Write a summary about inequalities.
Hint:
Check your summary:
- Do you explain what each inequality symbol represents?
- For each symbol, do you describe how to write an inequality using variables?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to learn whether students understand how an inequality and an equation are similar.
SWD: Some students may struggle to initiate writing for this reflection. Prompt them to refer to the sentence starter as a support and provide scaffolding questions or a list of ideas that were discussed in class. In addition to the sentence starter, students may also benefit from paragraph frames such as “So far, I have completed.… I have noticed that.… The parts I found challenging were.…”
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I think an inequality is similar to an equation because …