- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Reasoning to Identify Solutions

Overview
Lesson Overview
Students use reasoning to identify solutions to equations. They initially do this using the balance scale. They also learn that some equations may have all numbers as solutions and some equations may have no solutions.
Key Concepts
Before beginning the formal process of solving equations, students need opportunities to use reasoning to find solutions. Students study examples where reasoning pays off. For example, in the equation 4b + 15 = 3b + 6b, students can reason that 4b + 15 = 3b + 6b, so 5b must be equal to 15, an equation which they can solve by understanding multiplication.
Students also discover that there are equations that can have every number as a solution or no number as a solution. They may recognize some equations with all numbers as solutions by recognizing that they show a property of operations, such as the commutative property of addition.
SWD: Students with disabilities may struggle to determine salient information in lessons. Preview the goals with students to support saliency determination as they move through the instruction and tasks.
Students with disabilities may struggle to self-monitor their progress through the lesson. Provide students with a copy of the lesson goals to use as a checklist as they move through the different tasks. Have students indicate when they have reached each goal for the lesson. This will also promote engagement, independence, and self-management of learning.
Goals and Learning Objectives
- Use reasoning to identify the solution to an equation.
- Recognize equations that have any number as a solution and equations that have no solutions.
Reasoning to Find a Solution
Lesson Guide
Have students work in pairs to find the solution to x + 5x = 5x + 16. They will find that 16 is the only solution.
Ask students: Do you think there are any other numbers that are also solutions to the equation?
Allow students to share their reasoning. Some students may be beginning to discover some properties of equality on their own. For example, a student may reason that when both sides of the equation are balanced, if the same amount is removed from both sides, the equation will remain balanced. So, they may remove 5x from each side, leaving x = 16. They will realize that 16 is the only solution.
Do not attempt to teach such strategies at this time. The purpose of this lesson is for students to discover on their own some techniques for finding solutions to equations before any formal rules are introduced.
SWD: Investigative work is intended to be a time for students to grapple with the mathematics, and it is crucial that teachers only help students understand the tasks and not solve the problem.
Opening
Reasoning to Find a Solution
Look at this equation and think about its structure:
x + 5x = 5x + 16
- Does the structure give you a clue about the solution to the equation?
- Find a solution and check to make sure your solution is in fact the solution.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will use reasoning and substitution to find solutions to equations.
Opening
Use reasoning and substitution to find solutions to equations.
Find Solutions
Lesson Guide
Have students work in pairs on the card sort and the presentation. As students work to solve an equation, have them write down their steps so they can share their solution processes during Ways of Thinking.
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Identify students who use what they know about the commutative property of addition.
Look for students who begin by using the distributive property to expand 4(m + 3).
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Listen for student pairs who are able to justify their reasoning to their partner and who ask good questions about their partner's reasoning.
Mathematical Practice 7: Look for and make use of structure.
Look for students who may be correctly or incorrectly using the addition and multiplication properties of equality in an informal way.
Interventions
Student has difficulty getting started.
- Describe the task in your own words to your partner.
- What are you trying to find?
- Start with an equation card. Use reasoning to find the value of the variable that makes the two sides of the equation equal. Can you find the matching solution card?
- Start with an equation card. Substitute the numbers on the solution cards until you find one that makes the equation true.
Student determines an incorrect solution.
- What is the equation? What is the solution?
- How can you use substitution to check your solution?
Student finds one solution and immediately moves on to the next equation, without checking if there are additional solutions.
- Did you try more than one number?
- Why do you think the equation has only one solution?
ELL: Use a pace that is appropriate for ELLs when posing the questions from the Interventions, especially when using words that students have recently learned. Allow ELLs to use a dictionary if they wish.
Answers
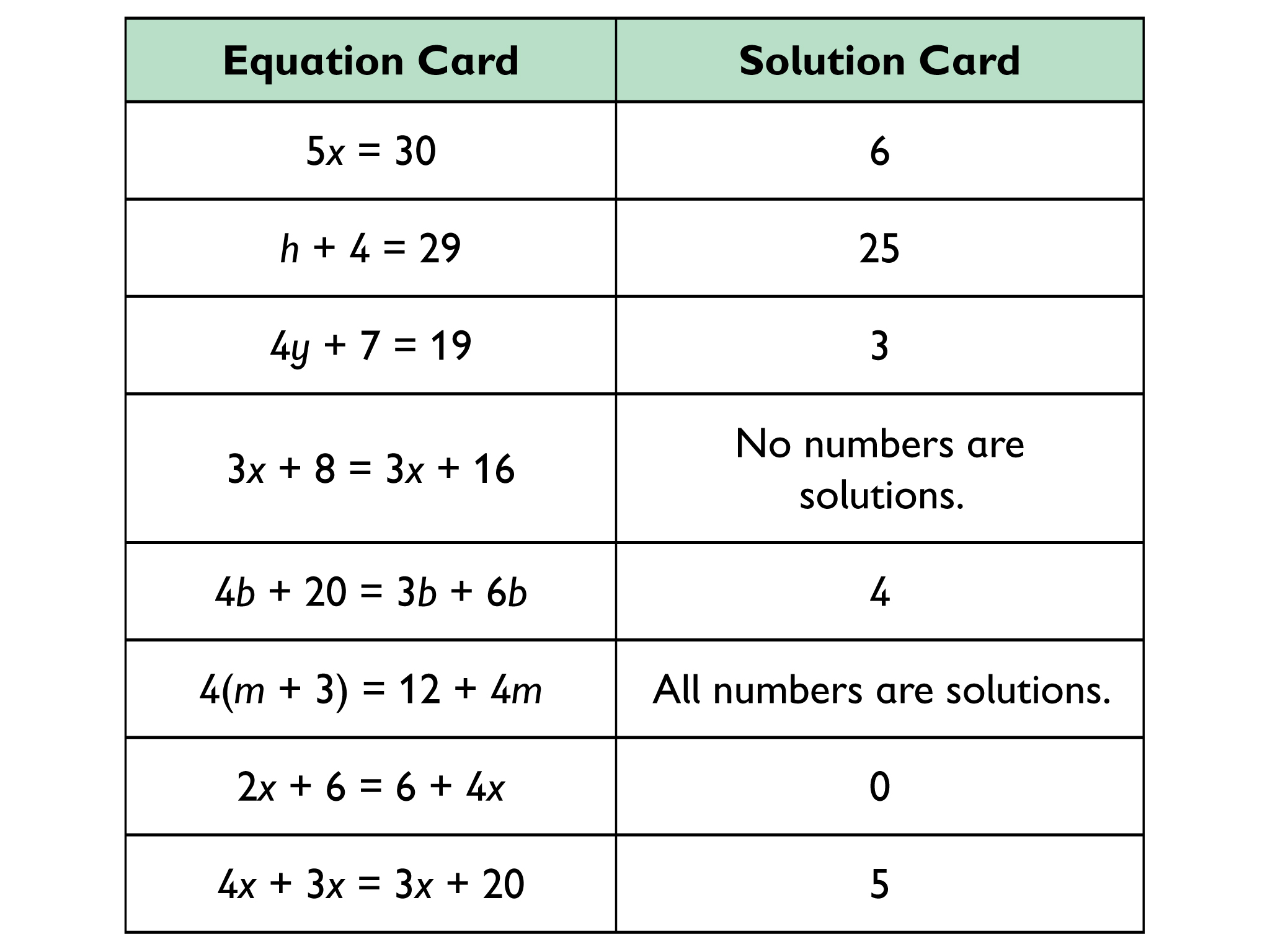
- Explanations will vary. Sample explanation: The cards match because the solution card is the solution to the equation; when it is substituted for the variable in the equation, the equation is true. If x = 6, and 6 is substituted for x in the equation 5x = 30, then 5(6) = 30 is true, so x = 6 is the solution and the cards match.
- Steps will vary.
Work Time
Find Solutions
- Take turns with your partner. Match an equation card with a solution card.
- Explain to your partner how you know that the cards match. Your partner should agree with your explanation or challenge it if your explanation is not correct, clear, and complete.
- Record the steps you took to find the solution for each equation.
HANDOUT: Card Sort
Hint:
- There is a value of the variable that makes the two sides of the equation equal. Think about what this value could be.
- Does the structure of the equation give you any clues about its solution?
- Try substituting different numbers on the solution cards into an equation to find the solution to that equation.
Prepare a Presentation
Lesson Guide
Students prepare presentations on strategies they used on the card sort in Task 3.
Preparing for Ways of Thinking
Listen as pairs work on the card sort. Identify students with different reasoning methods to share in the Ways of Thinking discussion.
Look for students who:
- Use the distributive property to state that 4(m + 3) is the same as 4m + 12.
- Suggest that all numbers are solutions to 4(m + 3) = 4m + 12 because of the commutative property of addition.
- State that all numbers are solutions to equations that have identical expressions on both sides of the equal sign.
- State that 3x + 8 = 3x + 16 has no solution because 8 does not equal 16.
- Are able to subtract the same amount from each side to simplify an equation.
- Informally use the addition and multiplication properties of equality.
- Systematically substitute the numbers on the solution cards into the equations to find the correct matches.
- State that they can check a solution by substituting the number for the variable in the equation to see if it produces a true equation.
Challenge Problem
Answers
- x = 3
- Explanations will vary. Sample answer: I know that my solution is correct because when I substitute 3 back into the equation for x, both sides of the equation are equal to 32, so they are equal to each other.
Work Time
Prepare a Presentation
Be prepared to share your matches and explain how you know that those cards match.
Challenge Problem
- Find a solution to this equation:
4x + 5 + 6x − 3 = 4(x + 5)
- Explain how you know your solution is correct and how you found it.
Make Connections
Lesson Guide
Have student pairs share their presentations. It is not necessary for students to use any formal equation-solving methods at this time. Make sure that a variety of solution strategies are presented.
Allow any students who attempted the Challenge Problem to share their solution strategy. If no one attempted a solution, work together to simplify the equation and then have students work in pairs to find the solution. A possible simplification might be 10x + 2 = 4x + 20.
Performance Task
Ways of Thinking: Make Connections
Take notes as your classmates explain how they matched the solution cards to the equation cards.
Hint:
As your classmates present, ask questions such as:
- How did you decide which number is a solution to
that equation? - Are there other solutions to that equation?
- Could you tell what the solution was from looking at the structure of the equation?
- Why do you think that equation has no solutions?
- Why do you think all numbers are a solution to that equation?
Solutions to Equations
A Possible Summary
Equations can have one solution, many solutions, or no solution. You can solve equations with one solution by guessing and checking or by reasoning about the equation. Equations with identical expressions on either side have all numbers as solutions. Equations with no values for the variable that make them true have no solution. You can check that a number is a solution to an equation by substituting the value for the variable to see if it is a true equation.
SWD: Students with disabilities may need review and reinforcement of the major skills and concepts covered in this lesson. Make sure students use this opportunity to review and reinforce their understanding of using substitution to check their solutions.
Formative Assessment
Summary of the Math: Solutions to Equations
Write a summary about finding solutions to equations.
Hint:
Check your summary:
- Do you explain how to find a solution to an equation?
- Do you explain how looking at the structure of an equation can help you find the solution?
- Do you explain how to show that a number is a solution to an equation?
- Do you provide examples of equations that have more than one solution or no solutions?
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to learn if students understand when an equation has more than one solution.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
An equation can have more than one solution when …