- Author:
- Chris Adcock
- Subject:
- Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Gallery Problems Exercise

Overview
Gallery Overview
Allow students who have a clear understanding of the content thus far in the unit to work on Gallery problems of their choosing. You can then use this time to provide additional help to students who need review of the unit's concepts or to assist students who may have fallen behind on work.
Gallery Descriptions
- Keep It Balanced
Students will use reasoning to complete some equations to make them true. - Equation Sort
Students will sort equations into three groups: equations with one solution, equations with many solutions, and equations with no solutions - On the Number Line
Students will use a number line to identify numbers that make an equation or inequality true. - How Many Colors?
Students will write and solve an equation to find the number of different colored blocks in a box. - Value of s
Students will use a property of equality to solve an equation with large numbers. - Marbles in a Cup
Students are given information about the weight of a cup with two different amounts of marbles in it. They use this information to find the weight of the cup. - When Is It True?
Students will use what they know about 0 and 1 to decide when a certain equation is true.
Keep It Balanced
Answers
- 3x + 5 = 5 + [3x]
4x + 5 = [5] + 3x + x
[6] + 2x = 2(x + 3)
3x + [2x] + 5 = 2 + 3 + 5x
6x + 3 + 3 = 6 + 3x + 2x + [x]
4(2x + 3) = 8x + 5 + [7]
2. Explanations will vary.
3. See answer to problem 1.
Opening
Keep It Balanced
Work with a partner.
- Take turns finding the card that belongs in the equation to make it a true equation.
- Explain to your partner how you made your decision. Your partner should either agree with your explanation or challenge it if your explanation is not clear, correct, and complete.
- When you both agree, write the appropriate card into the equation.
HANDOUT: Card Sort
Equation Sort
Answers
Explanations will vary.
- For the commutative property of addition states that this equation is true.
Answers will vary. Possible answer:
- Change to and now it will have many solutions.
Work Time
Equation Sort
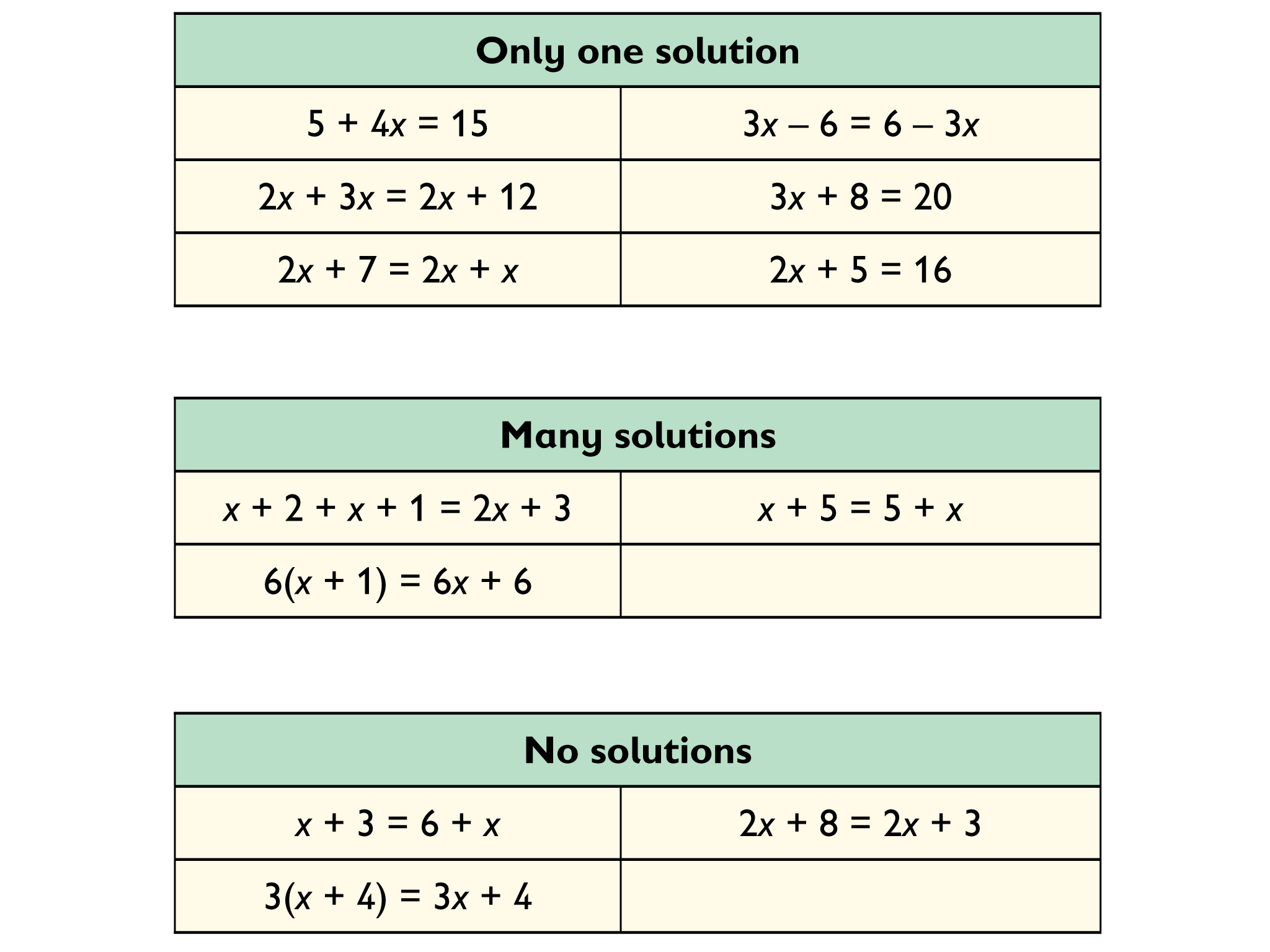
Sort the equations into three groups:
Equations with only one solution
Equations with many solutions
Equations with no solutions
Explain how you know where the equation should be placed.
Take one of the equations and change it so that it has a different number of solutions.
Equations:
2x + 5 = 16
6(x + 1) = 6x + 6
3(x + 4) = 3x + 4
2x + 3x = 2x + 12
x + 5 = 5 + x
5 + 4x = 15
2x + 8 = 2x + 3
2x + 7 = 2x + x
3x + 8 = 20
3x – 6 = 6 – 3x
x + 3 = 6 + x
x + 2 + x + 1 = 2x + 3
On the Number Line
Answers
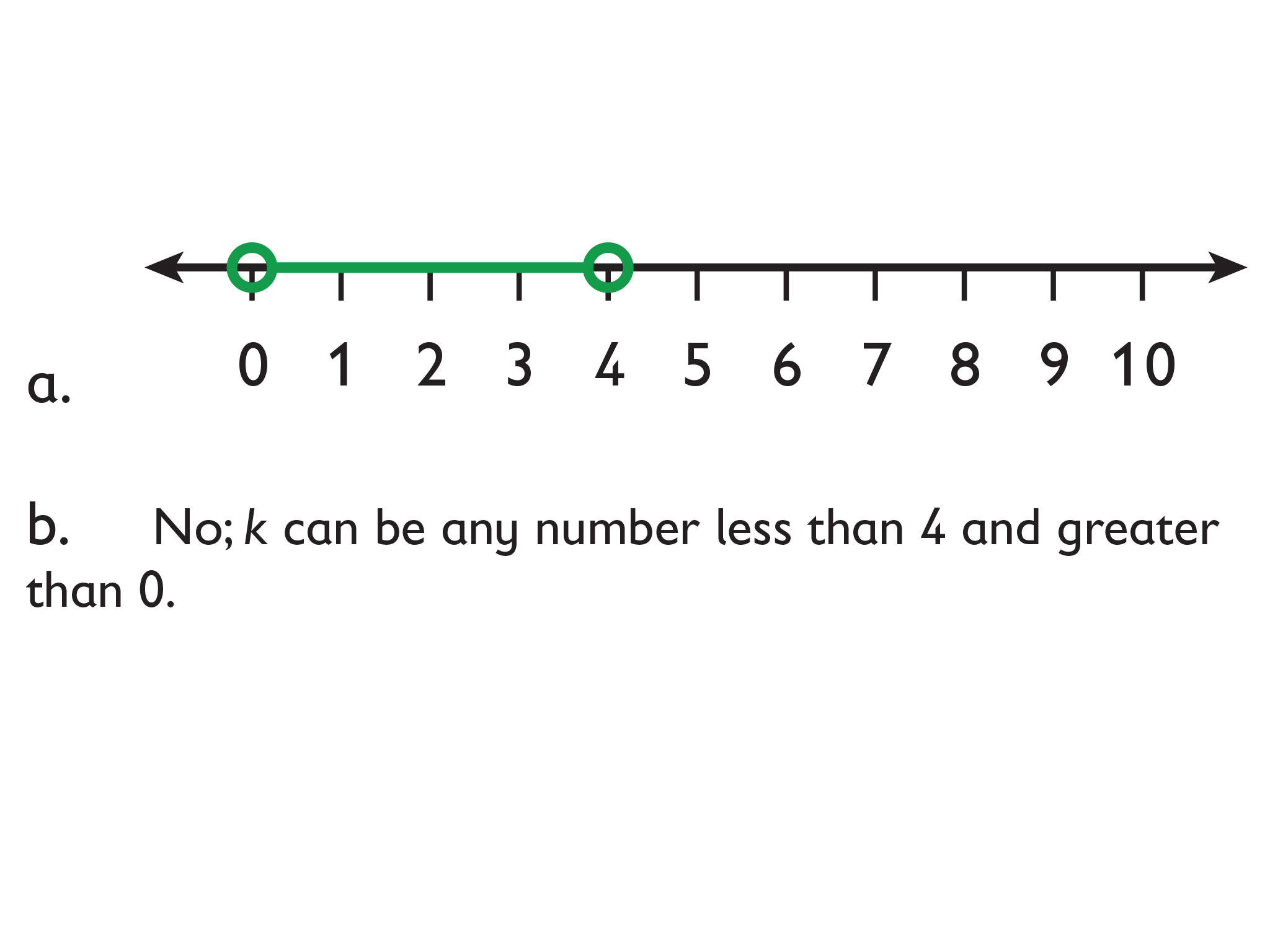
- Possible answer: 5
Possible answer: 3
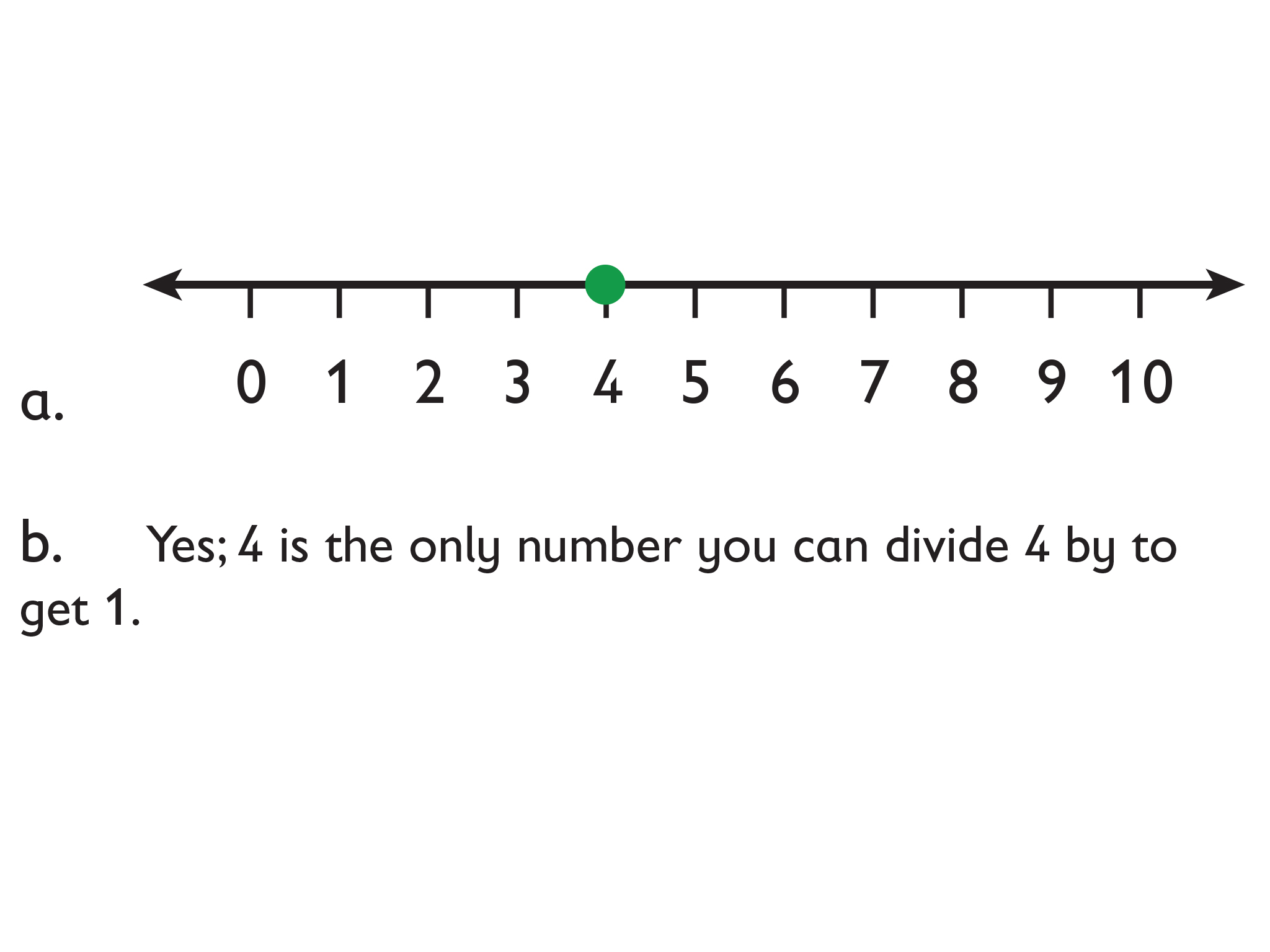
Answer: 4
Work Time
On the Number Line
Look at the portion of the number line shown. Use it to help you do problems 1–3. Either copy the number line to your Notebook, or draw your own number line to show your answers.
- Find a value for j that makes true.
- Mark this value of j on a number line.
- Is your value the only one possible? If so, say why. If not, describe the set of possible values.
2. Find a value for k that makes true.
- Mark this value of k on a number line.
- Is your value the only one possible? If so, say why. If not, describe the set of possible values
3. Find a value for m that makes true.
- Mark this value of m on a number line.
- Is your value the only one possible? If so, say why. If not, describe the set of possible values.
How Many Colors?
Answers
1. There are five different colors of blocks in a box.
n = number of blocks = 40
s = number of shapes = 4
t = number of sizes = 2
c = number of colors
To find the number of unique shape-size-color combinations, multiply the three variables together.
cst = n
2.
c(4)(2) = 40
c(8) = 40
Multiplication property of equality
c = 5
Work Time
How Many Colors?
A child sees a box of blocks in a store. The child notices these things:
- There are four different shapes.
- There are two different sizes.
- There are several different colors.
- There are 40 blocks in the box.
- There is exactly one block of each “shape-size-color” combination.
- Write an equation to find the number of colors in the box.
- Solve your equation and show your work.
Value of s
Answers
- The efficient way to find s:
- Because of the addition property of equality, the equation can be solved by subtracting 249 from both sides.
Work Time
Value of s
- Show an efficient way to find the value of s + 249 = 47,921.
- Explain why your method works to find the value of s.
Marbles in a Cup
Answers
- w = nm + c
- w = mass of cup and marbles together
n = number of marbles in a cup
m = mass of a marble in grams
c = mass of the cup in grams
12m + c = 147
15m + c = 165
So, 3 marbles must have a mass of 165 − 147, or 18 grams.
12m = 4 × 18 = 72
15m = 5 × 18 = 90
So, 72 + c = 147, or 90 + c = 165
Using either equation, the cup has a mass of 75 grams.
Work Time
Marbles in a Cup
Chen has some marbles that are all identical.
He puts 12 marbles in a cup. The marbles and the cup together have a mass of 147 grams.
When he puts 15 marbles in the cup, he finds that the marbles and the cup together have a mass of 165 grams.
Let n = the number of marbles in the cup. Let m = the mass of a marble in grams. Let c = the mass of the cup in grams.
- Write a formula for w, the mass in grams of the cup and the marbles together, using just the variables but no numbers.
- What is the mass of the cup in grams? Show how you got your answer.
When Is It True?
Answers
- The equation a + 0 = 1 • a is always true.
- If you add 0 to any number, you get that number.
If you multiply any number by 1, you get that number.
So, both sides of the equation equal a; a = a.
Work Time
When Is It True?
- When is this equation true? Always? Sometimes? Or never?
a + 0 = 1 • a - Show or explain why.